Схемы дедуктивных умозаключений

Введение

 

Большую часть знаний об окружающей нас действительности мы получаем с помощью рассуждений. Знание будет истинным, если оно получено путем правильного рассуждения, а таким считают рассуждение, построенное по правилам логики.

Рассуждения лежат в основе доказательства, без которого трудно представить математику. Но тех представлений о доказательстве, которые возникли у вас в процессе конкретных доказательств, конечно, недостаточно, чтобы обучать доказательству младших школьников. Учителю нужны более глубокие знания о тех правилах, в соответствии с которыми строятся правильные рассуждения, нужны знания о структуре и способах доказательства, о взаимосвязи индукции и дедукции.

 

Умозаключения и их виды

В логике вместо термина «рассуждения» чаще используются (как его синоним) слово «умозаключение», им и будем пользоваться.

Умозаключение - это способ получения нового знания на основе некоторого имеющегося. При этом мы не обращаемся к исследованию предметов и явлений самой действительности, а открываем такие связи и отношения между ними, которые невозможно увидеть непосредственно.

Умозаключение состоит из посылок и заключения.

Посылки - это высказывания, содержащие исходное знание.

Заключение - это высказывание, содержащее новое знание, полученное из исходного. В умозаключении из посылок выводится заключение.

Рассмотрим примеры умозаключений, которые выполняют младшие школьники, изучая математику.

П р и м е р 1. Ученику предлагается объяснить, почему число 23 можно представить в виде суммы 20 + 3. Он рассуждает: Число 23 - двузначное. Любое двузначное число можно представить в виде суммы разрядных слагаемых. Следовательно, 23 = 20 + 3».

Первое и второе предложения в этом умозаключении посылки, причем одна посылка общего характера - это высказывание «любое двузначное число можно представить в виде суммы разрядных слагаемых», а другая - частная, она характеризует только число 23 - оно двузначное. Заключение - это предложение, которое стоит после слова «следовательно», - также носит частный характер, так как в нем речь идет о конкретном числе 23.

П р и м е р 2. Один из приемов ознакомления младших школьников с переместительным свойством умножения заключается в следующем. Используя различные средства наглядности, школьники вместе с учителем устанавливают, что 6·3 = 3·6, 5·2 = 2·5, 3·7 = 7·3. А затем, на основе полученных равенств делают вывод: для всех натуральных чисел а и b верно равенство ab = ba.

В данном умозаключении посылками являются первые три равенства, в них утверждается, что для конкретных натуральных чисел выполняется такое свойство. Заключением в данном примере является утверждение общего характера - переместительное свойство умножения натуральных чисел.

П р и м е р 3. При обучении делению на однозначное число используется такой прием. Сначала выясняется: чтобы найти значения высказывания 12:4, следует узнать, на какое число надо умножить делитель 4, чтобы получить делимое, т.е. 12. Известно, что 4-3 = 12. Значит, 12:4 = 3.

Затем учащимся предлагается, рассуждая так же, найти, например, частное 8:4. И они сначала находят число, на которое надо умножить 4, чтобы получить 8. Получают число 2 и делают вывод - 8:4 = 2.

Далее, используя тот же способ рассуждений, находят частные 9:3,20:5 и др.

Видим, что умозаключения бывают разные. В примере 1 заключение логически следует из посылок, и мы не сомневаемся в его истинности. Такие умозаключения называют в логике дедуктивными.

О п р е д е л е н и е. Дедуктивным называется умозаключение, в котором посылки и заключение находятся в отношении логического следования.

Если посылки дедуктивного умозаключения обозначить буквами A₁, А₂, ... , А_n, а заключение - буквой В, то схематично само умозаключение можно представить так: A_1, А₂, ... А_n => В.

Часто используют такую запись: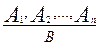

В ней черта заменяет слово «следовательно».

Дедуктивным является умозаключение, которое рассмотрено в примере 1.

Более подробно такие умозаключения мы рассмотрим позже, в пункте 26, а пока заметим, что в дедуктивном умозаключении всегда, когда истинны посылки, истинно и заключение.

Умозаключение, которое рассмотрено в примере 2, отлично от первого. В нем приведены три посылки частного характера, которые показывают, что некоторые натуральные числа обладают свойством: от перестановки множителей произведение не изменяется. И на этой основе сделан вывод, что этим , свойством обладают все натуральные числа. Такие умозаключения называют неполной индукцией.

О п р е д е л е н и е. Неполная индукция- это умозаключение, в котором на основании того, что некоторые объекты класса обладают определенным свойством, делается вывод о том, что этим свойством обладают все объекты данного класса.

Неполная индукция не является дедуктивным умозаключением, поскольку, рассуждая по такой схеме, можно прийти к ложному выводу.

Рассмотрим, например, такие выражения 3 + 5 и 3 · 5; 2 + 7 и 2 · 7; 4 + 8 и 4 · 8. Видим, что 3 + 5 < 3 · 5, 2 + 7 < 2 · 7,4 + 8 < 4 · 8, т.е. для некоторых натуральных чисел можно утверждать, что сумма меньше их произведения. И на основании того, что некоторые числа обладают указанным свойством, можно сделать вывод о том, что этим свойством обладают все натуральные числа, т.е. ( 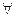a, b N) a + b<a·b.

Но это утверждение ложно, в чем можно убедиться с помощью контрпримера: числа 1 и 2 - натуральные, но сумма 1 + 2 не меньше, чем произведение 1·2.

Вообще к выводам, полученным с помощью неполной индукции, надо относиться критически, так как они носят характер предположения, гипотезы и нуждаются в дальнейшей проверке: их надо либо доказать, либо опровергнуть.

Несмотря на то что неполная индукция не всегда приводит к истинным выводам, роль таких умозаключений в процессе познания велика. Почти все общие положения и, в частности, научные законы являются результатом умозаключений, называемых неполной индукцией.

Третий пример - это пример рассуждения по аналогии.

Слова «аналогия» в переводе с греческого означает «соответствие, сходство».

Вообще под аналогией понимают умозаключение, в котором на основании сходства двух объектов в некоторых признаках и при наличии дополнительного признака у одного из них делается вывод о наличии такого же признака у другого объекта.

Заметим, что в этом описании сути понятия «аналогия» термин «объект» используется в широком смысле: им может быть реальный предмет, модель, рисунок, числовое или буквенное выражение, задача и т.д. В качестве признаков могут выступать свойства объектов, отношения между ними, способы деятельности и т.д.

Аналогия помогает открывать новые знания, способы деятельности или использовать усвоенные способы деятельности в измененных условиях.

Вывод по аналогии носит характер предположения, гипотезы и поэтому нуждается либо в доказательстве, либо в опровержении.

Например, ученик установил, что число делится на 6, если оно делится на 2 и на 3. Затем, действуя по аналогии, сделал вывод: число делится на 8, если оно делится на 2 и на 4. Чтобы убедиться в ложности полученного вывода, достаточно привести контрпример: число 12 делится на 2 и на 4, но не делится на 8.

Широко используется аналогия в обучении математике младших школьников. Это происходит при изучении свойств объектов, отношений между ними и действий с ними. Приведем несколько примеров.

Аналогию можно использовать для «открытия» новых свойств изучаемых объектов. Например, если при изучении классов установлено, что в классе единиц три разряда - единицы, десятки, сотни, а в классе тысяч также три разряда -единица тысяч, десятки тысяч, сотни тысяч, то вывод о числе разрядов в классе миллионов и их названии дети могут сделать самостоятельно, по аналогии.

Аналогия может быть использована для установления отношений между данными объектами. Например, учащиеся установили, что 4· (3 + 7) > 4·3 + 4·6, так как 4· (3 + 7) = 4·3+4·7, а 4·7 > 4·6. Рассматривая затем выражения 3(8 + 9) и 3·8 + 3·7, учащиеся могут по аналогии сделать вывод о том, что 3 · (8 + 9) > 3 ·8 + 3·7. Проверить его правильность можно либо путем рассуждений, аналогичных тем, что проводились при выполнении первого задания либо при помощи вычислений.

Аналогия может быть использована и для выводов о способе действия на основе изучения другого способа. Так, после рассмотрения способа умножения двузначного числа на однозначное на примере умножения 27 на 3 (27·3 =

= (20+7) ·3 = 20·3+7·3 = 81) детям предлагается умножить 721 на 4. Действуя по аналогии, они устанавливают, что 712·4= (700+ 10 + 2) ·4 = 2800 + 40+8 = 2848. Далее по аналогии устанавливают, как умножить 6288 на 3.

Следующим шагом может быть обобщение, т.е. получение правила умножения многозначного числа на однозначное, т.е. использование неполной индукции.

 

Схемы дедуктивных умозаключений

Рассмотрим подробнее дедуктивные (правильные) умозаключения. Согласно определению (п. 25) в дедуктивном умозаключении посылки и заключение находятся в отношении логического следования. Это означает, что в нем всегда из истинных посылок следует истинное заключение. Но как строить такие умозаключения и проверять их правильность?

В логике считают, что правильность умозаключения определяется его формой и не зависит от конкретного содержания входящих в него утверждений. И в логике предлагаются такие правила, соблюдая которые, можно строить дедуктивные умозаключения. Эти правила называют правилами вывода или схемами дедуктивных (правильных) умозаключений. Правил много, но наиболее часто используются следующие:

 

Выясним, что обозначают все знаки, использованные в записи этих правил; как их применять на практике.

Рассмотрим, например, правило заключения. В нем обозначены две посылки А(х) => В(х) и А(а). Первую называют общей посылкой, это может быть теорема, определение и, вообще, предложение вида А(х) => В(х). Вторую посылку А (а) называют частной, она получается из условия А(х) при х = а. Предложение В(а) - это заключение, оно получается из В(х) при х = а. Посылки отделены от заключения чертой, которая заменяет слово «следовательно».

Приведем пример умозаключения, выполненного по правилу заключения:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Запись числа 135 оканчивается цифрой 5. Следовательно, число 135 делится на 5.

В качестве общей посылки в этом умозаключении выступает утверждение вида «если А(х), то В(х)», где А(х) - это «запись числа д: оканчивается цифрой 5», а В(х) - «число х делится на 5». Частная посылка представляет собой высказывание, которое получилось из условия общей при jc = 135 (т.е. это Л(135)). Заключение является высказыванием, полученным из В(х) при х - 135 (т.е. это 5(135)).

Приведем теперь пример умозаключения, выполненного по правилу отрицания:

Если запись числа х оканчивается цифрой 5, то число х делится на 5. Число 177 не делится на 5. Следовательно, оно не оканчивается цифрой 5.

Видим, что в этом умозаключении общая посылка такая же, как и в предыдущем, а частная представляет собой отрицание высказывания «число 177 делится на 5 (т.е. это ).

Заключение- это отрицание предложения «Запись числа 177 не оканчивается цифрой 5» (т.е. ).

И, наконец, рассмотрим пример умозаключения, построенного по правилу силлогизма.

Если число х кратно 12, то оно кратно 6. Если число х кратно 6, то оно кратно 3. Следовательно, если число х кратно 12, то оно кратно 3.

В этом умозаключении две посылки вида «если А(х), то В(х)» и «если В(х), то С(х)», где А(х)- это предложение «х кратно 12», В(х) - предложение «х кратно 6» и С(х) - предложение «х кратно 3». Заключение представляет собой высказывание «если А (х), то С(х)».

Конечно, возникает вопрос, почему умозаключения, выполненные по правилам заключения, отрицания и силлогизма, будут дедуктивными (правильными)? Дело в том, что, выполняя рассуждения по этим правилам, мы всегда будем получать истинное заключение, что и требуется в дедуктивном умозаключении. Убедиться в этом можно, если воспользоваться кругами Эйлера.

В логике существуют различные способы проверки правильности умозаключений. Мы рассмотрим тот, который предполагает использование кругов Эйлера. Сначала данное умозаключение записывают на теоретико-множественном языке, затем посылки изображают на кругах Эйлера, считая их истинными. После этого выясняют, всегда ли при таких посылках истинно заключение. Если оказывается, что всегда, то говорят, что данное умозаключение правильное, дедуктивное. Если же возможен рисунок, из которого видно, что заключение может быть ложным, то говорят, что всякое умозаключение, выполненное по такой схеме, является недуктивным, неправильным.

Покажем, что умозаключение, выполненное по правилу заключения, является дедуктивным. Сначала запишем это правило на теоретико-множественном языке.

Посылка А (х) => В(х) может быть записана в виде Т_а Т_в, где Т_а и Т_в - множества истинности высказывательных форм А(х) и В(х).

Частная посылка А(а) означает, что а Т_а, а заключение В(а) показывает, что а Т_в.

Все умозаключение, построенное по правилу заключения, запишется на теоретико-множественном языке так:

Изобразив на кругах Эйлера множества Т_а и Т_в, и обозначив элемент а Т_а, мы увидим, что а Т_в (рис. 37),т.е.а Т_а =>а Т_в.

Аналогичным образом можно проверить и другие правила дедуктивных умозаключений. Кроме того, такой способ проверки правильности умозаключений можно использовать и в тех случаях, когда умозаключение

выполнено по схеме, отличной от рассмотренных.

 

З а д а ч а. Правильно ли следующее умозаключение: «если запись числа оканчивается цифрой 5, то число делится на 5. Число 125 делится на 5. Следовательно, запись числа 125 оканчивается цифрой 5».

Р е ш е н и е. Это умозаключение выполнено по схеме

которую в общем виде можно представить так:

Но такой схемы среди названных выше нет. Является ли она правилом дедуктивного умозаключения?

Чтобы ответить на этот вопрос, воспользуемся кругами Эйлера. На теоретико-множественном языке полученное правило можно записать так:

Изобразим на кругах Эйлера множества Т_а и Т_в и обозначим элемент а, принадлежащий множеству Т_в. Но оказывается, что он может содержаться в множестве ТА, а может и не принадлежать ему (рис. 38).

 

В логике считают, что такая схема не является правилом дедуктивного умозаключения, так как она не гарантирует истинности заключения. И вообще при анализе умозаключения нельзя отождествлять правильность умозаключения с истинностью полученного заключения: заключение

может быть истинным, а само умозаключение не быть дедуктивным, правильным.

Возвращаясь к вопросу нашей задачи, скажем, что данное в ней умозаключение не является правильным, так как выполнено по схеме, не гарантирующей истинности заключения.

Как же надо действовать, чтобы установить, правильно ли умозаключение или нет? Для этого есть два пути. Первый - это показать, что данное умозаключение выполнено по одному из известных правил вывода. Второй - сформулировать данное умозаключение на теоретико-множественном языке и воспользоваться кругами Эйлера так, как описано выше.

Полезно также запомнить и не путать с правилом заключения такую схему:

а с правилом отрицания схему:

Эти схемы не гарантируют истинности заключения и, следовательно, не являются правилами дедуктивных умозаключений.

Заметим, что полное дедуктивное умозаключение по приведенным трем правилам требует указания двух посылок. Однако в процессе рассуждений эти правила иногда сокращают, опуская одну из посылок. Например, объясняя, почему 6 < 8, ученик говорит, что «6 при счете называют раньше, чем 8, значит, 6 < 8». Является ли это умозаключение дедуктивным? Если «да», то по какому правилу оно выполнено?

В объяснении ученика пропущена общая посылка: «если число а при счете называют раньше числа b, то а меньше b». Если ее восстановить, то умозаключение ученика примет вид: , и это правило заключения.

Заметим еще, что, выполняя умозаключения, можно менять очередность посылок и можно начинать с заключения, а потом воспроизводить посылки.

Заметим также, что если общие посылки рассмотренных в правилах дедуктивных умозаключений содержат более одной переменной, то это не нарушает смысла этих правил.