Исследование функций и построение графиков
I. Методические указания и примеры
Теорема 4.1(достаточный признак монотонности функции). Если производная функции 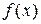 неотрицательна (неположительна) на интервале (а, b), то данная функция возрастает (убывает) на этом промежутке.
неотрицательна (неположительна) на интервале (а, b), то данная функция возрастает (убывает) на этом промежутке.
Теорема 4.2(необходимые условия существования экстремума).Если функция 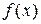 имеет в точке
имеет в точке 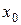 из интервала (а, b) экстремум, то либо
из интервала (а, b) экстремум, то либо  , либо
, либо  , либо
, либо  не существует.
не существует.
Определение 4.1.Точки из области определения функции 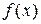 , в которых её производная равна нулю, бесконечности, или не существует, называются критическими точками данной функции (иначе точками, подозрительными на экстремум). Точки, где производная
, в которых её производная равна нулю, бесконечности, или не существует, называются критическими точками данной функции (иначе точками, подозрительными на экстремум). Точки, где производная  равна нулю, называют также стационарными точками.
равна нулю, называют также стационарными точками.
Определение 4.2. Экстремум функции 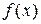 , достигаемый в стационарной точке, называется гладким экстремумом. Если в точке экстремума не существует
, достигаемый в стационарной точке, называется гладким экстремумом. Если в точке экстремума не существует  , но существуют неравные между собой односторонние производные, то такой экстремум называется угловым. Если в точке экстремума производная бесконечна, то он называется острым.
, но существуют неравные между собой односторонние производные, то такой экстремум называется угловым. Если в точке экстремума производная бесконечна, то он называется острым.

|

 Например, функция
Например, функция  имеет в точке (1, е +2) гладкий экстремум, касательная к её графику в этой точке параллельна оси Оx (рис. 4.1). Функция
имеет в точке (1, е +2) гладкий экстремум, касательная к её графику в этой точке параллельна оси Оx (рис. 4.1). Функция  имеет в точках (1,
имеет в точках (1,  ) и (–2,
) и (–2,  ) острые экстремумы, касательные к графику в этих точках параллельны оси Оy (в них производная бесконечна, рис. 4.2). Функция
) острые экстремумы, касательные к графику в этих точках параллельны оси Оy (в них производная бесконечна, рис. 4.2). Функция  имеет в точке (–1, /2) угловой экстремум, её график в этой точке имеет только односторонние касательные (в точке экстремума производной не существует, рис. 4.3).
имеет в точке (–1, /2) угловой экстремум, её график в этой точке имеет только односторонние касательные (в точке экстремума производной не существует, рис. 4.3).

|
| |||
 | |||
|



|
|
|
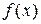 непрерывна в некоторой окрестности критической точки
непрерывна в некоторой окрестности критической точки 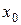 и дифференцируема во всех точках этой окрестности за исключением, быть может, самой точки
и дифференцируема во всех точках этой окрестности за исключением, быть может, самой точки 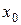 . Если при переходе аргумента х через эту точку слева направо производная
. Если при переходе аргумента х через эту точку слева направо производная  меняет знак, то в точке
меняет знак, то в точке 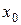 функция
функция 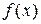 имеет экстремум (при изменении знака
имеет экстремум (при изменении знака  с плюса на минус – максимум, с минуса на плюс – минимум).
с плюса на минус – максимум, с минуса на плюс – минимум).
|

Например, для функции  её первая производная
её первая производная

равна нулю при  , а в точке
, а в точке  данная функция имеет неравные между собой односторонние производные
данная функция имеет неравные между собой односторонние производные  и
и  . Точки
. Точки  и
и  – критические для данной функции, при этом точка
– критические для данной функции, при этом точка  является также стационарной точкой, а в точке
является также стационарной точкой, а в точке  производной не существует. При переходе через точку
производной не существует. При переходе через точку  слева направо производная
слева направо производная  меняет знак с плюса на минус, а при переходе через точку
меняет знак с плюса на минус, а при переходе через точку  производная меняет знак с минуса на плюс. Поэтому функция в точке
производная меняет знак с минуса на плюс. Поэтому функция в точке  имеет гладкий максимум, а в точке
имеет гладкий максимум, а в точке  – угловой минимум (на рис. 4.4 в точке (2, 0) изображены односторонние касательные T1, T2).
– угловой минимум (на рис. 4.4 в точке (2, 0) изображены односторонние касательные T1, T2).
Определение 4.3.График Гфункции 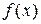 , дифференцируемой на интервале (а, b), называется выпуклым вверх (вниз) на этом промежутке, если он расположен ниже (выше) касательной, проведённой к Гв любой его точке
, дифференцируемой на интервале (а, b), называется выпуклым вверх (вниз) на этом промежутке, если он расположен ниже (выше) касательной, проведённой к Гв любой его точке  , где
, где  .
.
Теорема 4.4 (достаточное условие выпуклости графика функции на интервале).Если функция 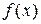 дважды дифференцируема на интервале (а, b) и
дважды дифференцируема на интервале (а, b) и  всюду на этом интервале, то график этой функции на интервале (а, b) является выпуклым вверх (вниз).
всюду на этом интервале, то график этой функции на интервале (а, b) является выпуклым вверх (вниз).
Например, пусть  , тогда
, тогда 
 и
и 
 . Поскольку
. Поскольку  на промежутках
на промежутках 
 и
и  на промежутке
на промежутке  то на промежутках
то на промежутках 
 график функции направлен выпуклостью вверх, а на промежутке
график функции направлен выпуклостью вверх, а на промежутке  – выпуклостью вниз (рис. 4.5).
– выпуклостью вниз (рис. 4.5).

| 
|
Рис. 4.5. График функции 
| Рис. 4.6. График функции 
|
Определение 4.4.Пусть функция 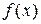 непрерывна на некоторой окрестности U(
непрерывна на некоторой окрестности U(  ) точки
) точки 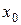 и дифференцируема на U(
и дифференцируема на U(  ) за исключением, быть может, самой точки
) за исключением, быть может, самой точки 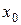 . Если при переходе аргумента х через эту точку меняется направление выпуклости графика Гэтой функции, то точка
. Если при переходе аргумента х через эту точку меняется направление выпуклости графика Гэтой функции, то точка  называется точкой перегиба графика Г.
называется точкой перегиба графика Г.
Так, для функции  точки (– 1, 1/4), (1, 1/4) – точки перегиба её графика (рис. 4.5).
точки (– 1, 1/4), (1, 1/4) – точки перегиба её графика (рис. 4.5).
Определение 4.5.Пусть функция 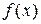 определена на некоторой окрестности точки
определена на некоторой окрестности точки 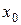 , кроме, быть может, самой точки
, кроме, быть может, самой точки 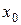 . Если хотя бы один из пределов
. Если хотя бы один из пределов  или
или  бесконечен, то прямая L:
бесконечен, то прямая L:  называется вертикальной асимптотой графика функции
называется вертикальной асимптотой графика функции 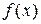 .
.
Например, прямая L: x = 1 – вертикальная асимптота графика функции  , так как односторонние пределы этой функции в точке x =1 бесконечны:
, так как односторонние пределы этой функции в точке x =1 бесконечны:  ,
,  (на рис. 4.6 изображён график этой функции и его вертикальная асимптота).
(на рис. 4.6 изображён график этой функции и его вертикальная асимптота).
Определение 4.6.Пусть функция 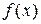 определена для сколь угодно больших по модулю значений аргумента х. Прямая L:
определена для сколь угодно больших по модулю значений аргумента х. Прямая L:  называется асимптотой графика данной функции при
называется асимптотой графика данной функции при  , если функция
, если функция 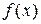 представима в виде:
представима в виде:
 , где
, где 
 при
при  .
.
Если угловой коэффициент k асимптоты L:  равен нулю, то она называется горизонтальной, если же
равен нулю, то она называется горизонтальной, если же  , то асимптота называется наклонной.
, то асимптота называется наклонной.
Теорема 4.5.Для того чтобы прямая L:  была асимптотой графика функции
была асимптотой графика функции 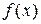 при
при  , необходимо и достаточно, чтобы существовали два предела:
, необходимо и достаточно, чтобы существовали два предела:
 ,
,  . (4.1)
. (4.1)
Эта теорема справедлива и для случая  , т. е. график функции может иметь различные асимптоты при
, т. е. график функции может иметь различные асимптоты при  и при
и при  .
.
 Например, исследуем функцию
Например, исследуем функцию  на наличие асимптот у её графика. Для этого вычисляем пределы (4.1):
на наличие асимптот у её графика. Для этого вычисляем пределы (4.1):
k =  =
=  .
.
Получаем два значения k: k1 = –1 при  и k1 = 1 при
и k1 = 1 при  . С каждым из них вычисляем второй из пределов (4.1):
. С каждым из них вычисляем второй из пределов (4.1):
b1=  =
=  = 0;
= 0;
b2 =  =
=  = 0.
= 0.
Итак, график данной функции имеет две наклонных асимптоты  при
при  и
и  при
при  (рис. 4.7).
(рис. 4.7).
Приведённые выше теоремы являются теоретической базой, используемой при построении графиков функций.
План исследования функции
1. Отыскание области определения данной функции  , установление свойств чётности (нечётности) и периодичности.
, установление свойств чётности (нечётности) и периодичности.
2. Отыскание точек пересечения графика функции с осями координат и промежутков знакопостоянства.
3. Исследование функции на непрерывность и существование асимптот.
4. Отыскание промежутков монотонности и точек экстремума.
5. Отыскание промежутков одинаковой направленности выпуклости графика функции и точек перегиба.
6. Построение математического эскиза графика функции и отыскание множества её значений.
Пример 4.1. Исследовать функции  и построить её график.
и построить её график.
1. 

 .
.
2. График пересекает оси координат в точках (2, 0) и (0, –4),  при
при  ,
,  при
при  .
.
3. Функция непрерывна на  как элементарная,
как элементарная,  – точка разрыва 2 рода (
– точка разрыва 2 рода (  ), прямая
), прямая  – вертикальная асимптота графика функции (определение 4.5). Вычисляя пределы (4.1), имеем:
– вертикальная асимптота графика функции (определение 4.5). Вычисляя пределы (4.1), имеем:
 ,
,

 .
.
Итак, прямая  – наклонная асимптота графика функции (теорема 4.5).
– наклонная асимптота графика функции (теорема 4.5).
 4.
4.  , на
, на  только две критические точки:
только две критические точки:  ,
,  . Вместе с точкой
. Вместе с точкой  они делят ось Ох на 4 промежутка: (– , –1), (–1, 1), (1, 2), (2, +). Знак
они делят ось Ох на 4 промежутка: (– , –1), (–1, 1), (1, 2), (2, +). Знак  в каждом из них приведён в таблице 4.1. Характер изменения функции указан стрелками, символ
в каждом из них приведён в таблице 4.1. Характер изменения функции указан стрелками, символ  – символ несуществования,
– символ несуществования,  – точка гладкого максимума, а в точке
– точка гладкого максимума, а в точке  нет экстремума, ибо
нет экстремума, ибо  не меняет знака при переходе аргумента х через эту точку.
не меняет знака при переходе аргумента х через эту точку.
 5.
5.  ,
,  – единственная точка, подозрительная на перегиб,
– единственная точка, подозрительная на перегиб,  . Вместе с точкой
. Вместе с точкой  она делит ось Ох на три промежутка:
она делит ось Ох на три промежутка:  (1, 2)
(1, 2)  . Знак
. Знак  в каждом из них приведён в таблице 4.2. В ней дугами указано направление выпуклости графика функции, (2, 0) – точка перегиба графика.
в каждом из них приведён в таблице 4.2. В ней дугами указано направление выпуклости графика функции, (2, 0) – точка перегиба графика.
6.Результаты проведённых исследований используем для построения графика данной функции. Сначала строим асимптоты, точку максимума и точку перегиба, затем строим график функции с учётом характера поведения функции на  (таблица 4.1) и направления выпуклости графика (таблица 4.2). График данной функции приведён на рис. 4.8, Е(f )=R.
(таблица 4.1) и направления выпуклости графика (таблица 4.2). График данной функции приведён на рис. 4.8, Е(f )=R.
Пример 4.2. Исследовать функцию  и построить её график.
и построить её график.
 1.D( f ) = R. Не выполняется ни одно из равенств: f (–x) = – f (x), f (–x) = f (x), данная функция не является чётной или нечётной – её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
1.D( f ) = R. Не выполняется ни одно из равенств: f (–x) = – f (x), f (–x) = f (x), данная функция не является чётной или нечётной – её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
2.f (x) = 0 Þ  Þ x = 1, график пересекает ось Oх в точке (1, 0). Для того чтобы найти ординату точки пересечения графика функции с осью Oy, вычислим f (0): f (0)
Þ x = 1, график пересекает ось Oх в точке (1, 0). Для того чтобы найти ординату точки пересечения графика функции с осью Oy, вычислим f (0): f (0)  . График пересекает ось Oу в точке (0,
. График пересекает ось Oу в точке (0,  ).
).
3.Данная функция непрерывна на D(f )= R как элементарная и, следовательно, её график не имеет вертикальных асимптот. Решая вопрос о существовании наклонных или горизонтальных асимптот, для данной функции вычислим пределы из равенств (4.1):
 ,
,

Значит, наклонных асимптот нет, а имеется одна горизонтальная асимптота  при
при  . Графически это означает, что при
. Графически это означает, что при  график данной функции неограниченно приближается к оси абсцисс, не пересекая её.
график данной функции неограниченно приближается к оси абсцисс, не пересекая её.
4.  при x = 2. Так как
при x = 2. Так как  на интервале (2, + ) и
на интервале (2, + ) и  на интервале (– , 2), то по теореме 4.2 в точке x = 2 функция имеет гладкий максимум (т.к.
на интервале (– , 2), то по теореме 4.2 в точке x = 2 функция имеет гладкий максимум (т.к.  ),
),  .
.
5.  при x = 3. Так как
при x = 3. Так как  на интервале (– , 3) и
на интервале (– , 3) и  на интервале (3, + ), то график функции в силу теоремы 4.4 на первом из этих интервалов направлен выпуклостью вверх, а на втором – выпуклостью вниз, точка (3, 2e–1) является точкой перегиба графика.
на интервале (3, + ), то график функции в силу теоремы 4.4 на первом из этих интервалов направлен выпуклостью вверх, а на втором – выпуклостью вниз, точка (3, 2e–1) является точкой перегиба графика.
6.По результатам проведённых исследований строится график данной функции (рис. 4.9), Е( f )=(– , 1].
Пример 4.3. Исследовать функцию  и построить её график.
и построить её график.
1.D( f ) = R. Не выполняется ни одно из равенств: f (–x) = – f (x), f (–x) = f (x), данная функция не является чётной или нечётной – её график не обладает симметрией ни относительно оси Оу, ни относительно начала координат.
 
 
  
|
|
 ). Кроме того, так как подкоренное выражение
). Кроме того, так как подкоренное выражение  при "хÎR, то f (x) 0 на всей D(y).
при "хÎR, то f (x) 0 на всей D(y).
3.Данная функция непрерывна на D( f ) = R как элементарная и поэтому её график не имеет вертикальных асимптот. Наклонных и горизонтальных асимптот также нет, поскольку
 .
.
4.  ,
,  при
при  ,
,  при x = –5 и x = 1. Функция имеет три критические точки:
при x = –5 и x = 1. Функция имеет три критические точки:  ,
,  и x = 1, они делят ось Ox на четыре интервала: (–, –5), (–5, –2), (–2, 1), (1, +). Определив на каждом из них знак
и x = 1, они делят ось Ox на четыре интервала: (–, –5), (–5, –2), (–2, 1), (1, +). Определив на каждом из них знак  , полученные результаты сведём в таблицу 4.3. В ней стрелками указан характер изменения функции на данном промежутке. В точке x = – 2 функция имеет гладкий максимум, в точках x = –5 и x = 1 функция имеет острые минимумы.
, полученные результаты сведём в таблицу 4.3. В ней стрелками указан характер изменения функции на данном промежутке. В точке x = – 2 функция имеет гладкий максимум, в точках x = –5 и x = 1 функция имеет острые минимумы.
Т а б л и ц а 4.3
| x | (– ¥, –5) | – 5 | (– 5, – 2) | –2 | (– 2, 1) | (1, +¥) | |

| – | ¥ | + | – | ¥ | + | |
| f (x) | æ | min | ä |  max
max
| æ | 0 min | ä |
5.  ,
,  при
при  ,
,  ,
,  ; f (x1)=f (x2)=
; f (x1)=f (x2)= 
 6.9. В точках x= –5 и x = 1 не существует
6.9. В точках x= –5 и x = 1 не существует  , так как в них первая производная бесконечна. Точки x = –5, x = 1 и
, так как в них первая производная бесконечна. Точки x = –5, x = 1 и  – точки подозрительные на перегиб. Они разбивают ось Ox на 5 интервалов: (–, –2–
– точки подозрительные на перегиб. Они разбивают ось Ox на 5 интервалов: (–, –2–  ), (–2–
), (–2–  , –5), (–5, 1), (1,–2+
, –5), (–5, 1), (1,–2+  ), (–2+
), (–2+  , +). Определив на каждом из них знак
, +). Определив на каждом из них знак  , полученные результаты сведём в таблицу 4.4. В ней дугами указан характер направления выпуклости графика функции на данном промежутке, символ
, полученные результаты сведём в таблицу 4.4. В ней дугами указан характер направления выпуклости графика функции на данном промежутке, символ  – символ несуществования.
– символ несуществования.
Т а б л и ц а 4.4
| x | (– ; x1) | x1 | (x1 ; –5) | –5 | (–5, 1) | (1 ; x2) | x2 | (x2 ; +) | |

| + | – | 
| – | 
| – | + | ||
| f (x) | È | »6.9 | Ç | Ç | Ç | »6.9 | È |
Точки с абсциссами х1, х2 – точки перегиба графика функции.
 6.По результатам проведённых исследований строится график данной функции (рис. 4.10), Е( f ) =[0, + ).
6.По результатам проведённых исследований строится график данной функции (рис. 4.10), Е( f ) =[0, + ).
II. Задачи для индивидуальных заданий.
Задача 1. Исследовать функцию  и построить её график.
и построить её график.
| 1.1. | 
| 1.2. |  . .
| |
| 1.3. |  . .
| 1.4. |  . .
| |
| 1.5. |  . .
| 1.6. |  . .
| |
| 1.7. |  . .
| 1.8. | 
| |
| 1.9. |  . .
| 1.10. | 
| |
| 1.11. |  . .
| 1.12. |  . .
| |
| 1.13. |  . .
| 1.14. |  . .
| |
| 1.15. | 
| 1.16. |  . .
| |
| 1.17. |  . .
| 1.18. |  . .
| |
| 1.19. |  . .
| 1.20. |  . .
| |
| 1.21. |  . .
| 1.22. |  . .
| |
| 1.23. |  . .
| 1.24. |  . .
| |
| 1.25. | 
| 1.26. | 
| |
| 1.27. | 
| 1.28. | 
| |
| 1.29. | 
| 1.30. | 
|
Задача 2. Исследовать функцию  и построить её график.
и построить её график.
| 2.1. | 
| 2.2. |  . .
|
| 2.3. |  . .
| 2.4. |  . .
|
| 2.5. |  . .
| 2.6. |  . .
|
| 2.7. |  . .
| 2.8. |  . .
|
| 2.9. |  . .
| 2.10. |  . .
|
| 2.11. |  . .
| 2.12. |  . .
|
| 2.13. |  . .
| 2.14. | 
|
| 2.15. |  . .
| 2.16. |  . .
|
| 2.17. |  . .
| 2.18. |  . .
|
| 2.19. |  . .
| 2.20. |  . .
|
| 2.21. |  . .
| 2.22. |  . .
|
| 2.23. |  . .
| 2.24. |  . .
|
| 2. 25 | 
| 2. 26 | 
|
| 2. 27 | 
| 2. 28 | 
|
| 2. 29 | 
| 2. 30 | 
|
Задача 3. Исследовать функцию  и построить её график.
и построить её график.
| 3.1. |  . .
| 3.2. |  . .
|
| 3.3. |  . .
| 3.4. |  . .
|
| 3.5. |  . .
| 3.6. |  . .
|
| 3.7. |  . .
| 3.8. |  . .
|
| 3.9. |  . .
| 3.10. |  . .
|
| 3.11. |  . .
| 3.12. |  . .
|
| 3.13. |  . .
| 3.14. |  . .
|
| 3.15. |  . .
| 3.16. |  . .
|
| 3.17. |  . .
| 3.18. |  . .
|
| 3.19. |  . .
| 3.20. |  . .
|
| 3.21. |  . .
| 3.22. |  . .
|
| 3.23. |  . .
| 3.24. |  . .
|
| 3.25. | 
| 3.26. | 
|
| 3.27. | 
| 3.28. | 
|
| 3.29. | 
| 3.30. | 
|
