
Категории:
АстрономияБиология
География
Другие языки
Интернет
Информатика
История
Культура
Литература
Логика
Математика
Медицина
Механика
Охрана труда
Педагогика
Политика
Право
Психология
Религия
Риторика
Социология
Спорт
Строительство
Технология
Транспорт
Физика
Философия
Финансы
Химия
Экология
Экономика
Электроника
Понятие о методе наименьших квадратов (МНК).
Лекция-7
ОСНОВЫ ЧИСЛЕННЫХ МЕТОДОВ
Метод наименьших квадратов
Понятие о методе наименьших квадратов (МНК).
Пусть имеются результаты некоторой серии экспериментов, в которой выявлено, например, попарное соответствие некоторых параметров 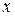 и
и 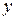 (см. таблицу 2.7.1, где
(см. таблицу 2.7.1, где  – номер опыта;
– номер опыта;  ,
,  – результаты эксперимента).
– результаты эксперимента).
Таблица 2.7.1. Результаты серии экспериментов.

| 
| 
| ||||
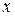
| 
| 
| … | 
| … | 
|
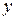
| 
| 
| … | 
| … | 
|
В таких случаях, как правило, целью эксперимента является выявление зависимости между величинами 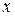 и
и 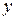 . Например, если экспериментальные точки на плоскости
. Например, если экспериментальные точки на плоскости  располагаются достаточно близко от некоторой кривой, то целесообразно получить аналитический вид этой кривой в виде
располагаются достаточно близко от некоторой кривой, то целесообразно получить аналитический вид этой кривой в виде  .
.
Чаще всего такая задача решается при условии, что задан (из каких-либо практических соображений) общий вид этой кривой (полином, экспонента, сумма синусоид или др.). Такая кривая, как правило, зависит от нескольких параметров. Определением этих параметров можно получить оптимальное (наилучшее) приближение искомой зависимости в классе заданного вида кривых.
Наиболее простым случаем является представление искомой зависимости в виде полинома, т.е. требуется найти полином  вида
вида
 (2.7.1)
(2.7.1)
заданной степени  , наилучшим образом отображающий полученную в эксперименте зависимость
, наилучшим образом отображающий полученную в эксперименте зависимость  от
от  .
.
Введем обозначения
 ,
,  (2.7.2)
(2.7.2)
– отклонения величин значений кривой  и точек эксперимента
и точек эксперимента  по координате
по координате 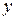 (рис. 2.7.1), соответствующих одному и тому же значению
(рис. 2.7.1), соответствующих одному и тому же значению  .
.

Рис. 2.7.1. Приближение результатов эксперимента некоторой кривой.
Оптимальной кривой будет такая, для которой эти отклонения будут минимальны. В качестве критерия минимума принимается минимум суммы квадратов отклонений по всем точкам эксперимента.
 (2.7.3)
(2.7.3)
В частности, когда искомая кривая представлена полиномом (2.7.1):
 . (2.7.4)
. (2.7.4)
Таким образом, задача сводится к определению минимума  , где уже
, где уже  является функцией от (
является функцией от (  +1)-ой переменной, т.е.
+1)-ой переменной, т.е.
 . (2.7.5)
. (2.7.5)
Из дифференциального исчисления известно, что условие минимума состоит в выполнении системы равенств
 ,
,  . (2.7.6)
. (2.7.6)
Распишем эти равенства, исходя из вида  (см. формулу (2.7.4)), получим:
(см. формулу (2.7.4)), получим:






 ,
,
 .
.
Следовательно, для определения коэффициентов оптимального полинома степени  требуется решить систему линейных уравнений (
требуется решить систему линейных уравнений (  +1)-го порядка:
+1)-го порядка:
 ,
,  . (2.7.7)
. (2.7.7)
Уравнения (2.7.7) называются нормальными уравнениями.
В частности, при  для получения коэффициентов оптимальной квадратичной параболы
для получения коэффициентов оптимальной квадратичной параболы  требуется решить систему линейных уравнений третьего порядка
требуется решить систему линейных уравнений третьего порядка
 (2.7.8)
(2.7.8)
Рассмотрим случай построения оптимальной прямой  (полином в случае
(полином в случае  )
)
Параметры прямой  и
и  определяются из системы уравнений:
определяются из системы уравнений:
 (2.7.9)
(2.7.9)
или, записанной в более привычном виде (в системе (2.7.9) поменяли местами уравнения и порядок неизвестных):
 (2.7.10)
(2.7.10)