Элементарные преобразования подынтегрального выражения.

Томский государственный университет систем управления и радиоэлектроники

Приходовский М.А.

Математика (курс практических занятий) 2 семестр

Учебное пособие для специальности

09.03.03 «прикладная информатика в экономике»

(группы 446-1, 446-2)

Томск

ТУСУР

 

Электронное пособие составлено и скорректировано с учётом реального проведения практических занятий на ФСУ в группах 446-1 и 446-2 весной 2017 года.

 

ПРАКТИКА № 1 (14.02.2017 у обеих групп).

Элементарные преобразования подынтегрального выражения.

Задача 1. Вычислить .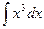

Решение.Известно, что 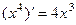. Для того, чтобы гарантированно правильно учесть коэффициент, лучше сразу домножить и поделить на 4, чтобы сформировать под знаком интеграла готовое выражение вида . Итак, = = = .

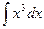Ответ. .

 

Задача 2. Вычислить .

Решение. Известно, что . При дифференцровании функций вида происходило умножение на константу, а при интегрировании наоборот, деление. Чтобы понять, почему это так, постараемся сначала сформировать внутри интеграла готовую производную от этой экспоненты, для чего домножим и поделим на 5.

= = = .

Ответ. .

Задача 3. Вычислить .

Решение. Замечая, что , преобразуем так:

= = = .

Ответ. .

Задача 4.Вычислить .

Решение. Известна формула . Если в знаменателе линейная функция вида , то можно добавить константу под знаком дифференциала, от этого ничего не изменилось бы, ведь производная константы это 0. Итак, = . Теперь интеграл имеет вид и конечно, равен . Фактически применили замену . Сделав обратную замену, получаем ответ: .

Ответ. .

Задача 5. Вычислить .

Решение.Здесь, в отличие от прошлой задачи, уже и в числителе есть переменная, то есть здесь неправильная дробь. Сначала нужно выделить целую часть дроби и отделить правильную дробь. В данном случае для этого достаточно прибавить и отнять 2 в числителе.

= = = =

= и теперь, когда разбили на сумму или разность табличных интегралов, получаем ответ: .

Ответ. .

Задача 6. Вычислить .

Решение.В данном случае неправильная дробь, причём степень в числителе более высокая. Можно применить общий метод выделения целой части, то есть поделить числитель на знаменатель.

Получили частное , остаток . Теперь можно представить в виде суммы интегралов:

= = .

Впрочем, можно и не делить столбиком, а просто отнять и прибавить 25, тогда = = что тоже приводит к .

Теперь, когда свели к сумме табличных интегралов, то с помощью уже ранее изученных действий получаем ответ:

Ответ. .

Задача 7.Вычислить .

Решение.Дискриминант знаменателя отрицательный, поэтому здесь невозможно сделать как в прошлой задаче, так как нет корней знаменателя и дробь невозможно свести к виду .

Но при D < 0 можно выделить полный квадрат:

= = .

С помощью замены сводится к интегралу:

= , и далее с помощью обратной замены получаем ответ.

Ответ. .

Задача 8. Вычислить .

Решение.В предыдущей задаче было D<0, а в этой D=0.

Выделяя полный квадрат, получим = .

В этом случае сводится не к арктангенсу, а к степенной функции, потому что получается = = .

Ответ. .

Задача 9. Вычислить .

Решение. В данном примере D>0, в отличие от предыдущих. Нужно сначала разбить дробь на сумму простейших:

и после этого, будет сумма двух таких интегралов, каждый из которых сводится к логарифму. Чтобы найти А и В, приведём к общему знаменателю:

= .

Теперь приравняем числители, ведь дроби равны, знаменатели одинаковы, значит и числители тоже:

.

Отсюда получается система уравнений, из которой можно найти неопределённые коэффициенты А и В:

Решая эту систему, получаем , . Тогда интеграл распадается на простейшие:

= = .

Ответ. .

Метод неопределённых коэффициентов подробнее будет изучаться в параграфе «интегрирование рациональных дробей», но его основная идея понятна уже из этой задачи.