Графическое представление эмпирического распределения
В результате сбора информации о эксплуатационной надежности (или получения соответствующего варианта исходных данных) у студента оказывается некоторая выборка наработок на отказ  . Наиболее наглядным является ее графическое представление. Методика его построения следующая.
. Наиболее наглядным является ее графическое представление. Методика его построения следующая.
1.1 Формирование ранжированного (в порядке возрастания) ряда из n исходных данных: 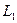 ,
,  , …
, …  .
.
158 619 793 1951 2229 2503 4632 4685 5311 5615 5941 8186 8289 9895 10586 11039 11355 12364 13696 14510 15143 15635 16298 18491 20472 20824 21438 22803 23395 23736 24177 24652 24901 25740 26122 26491 26662 27747 27924 28169 28308 28594 29315 29739 29836 30258 31638 31732 32504 33251 34416 34955 35031 35267 36141 37513 38182 39140 39694 41061
1.2 Выявление наименьшего и наибольшего значений выборки:
 ,
,  .
.
1.3 Определение размаха варьирования выборки R
 .
.
При объеме выборки п >50 обработку эмпирических данных рекомендуется вести по значениям, сгруппированным в К непересекающихся интервалов.
1.4 Определение приближенного количества интервалов группирования К
 .
.
Полученное значение округляется до целого числа в меньшую сторону.
1.5 Определение величины интервала группирования 
 .
.
1.6 Подсчет частот (частостей) попадания случайных величин в интервалы группирования 
 Вычисляются границы интервалов. Подсчитывается количество
Вычисляются границы интервалов. Подсчитывается количество  данных, находящихся в каждом из интервалов, и вычисляются соответствующие частости :
данных, находящихся в каждом из интервалов, и вычисляются соответствующие частости : 
Необходимо следить, чтобы в каждый интервал попадало не менее пяти данных, в противном случае интервал объединяется с соседним интервалом таким образом, чтобы число наработок на отказ в объединенном интервале было не менее пяти.
Результаты подсчета показаны в таблице 1
| № интервала, J | Границы интервалов (  ), км ), км
| Середина интервала,
 , км , км
| Частота попадания в интервал, 
| Частость попадания в интервал, 
| Эмпирическая плотность распределения

|
| 158-6975 | 0,18 | 
| |||
| 6975-13792 | 0,13 | 
| |||
| 13792-20609 | 0,1 | 
| |||
| 20609-27426 | 0,2 | 
| |||
| 27426-34243 | 0,22 | 
| |||
| 34243-41061 | 0,17 | 
|
1.7 Построение гистограммы и кривой распределения
Для графического изображения эмпирического распределения по
верхним граничным точкам или серединам интервалов строится график -
гистограмма, вид которого представлен на рисунке 1.


 L, км
L, км
 2 Определение основных статистических характеристик
2 Определение основных статистических характеристик
Числовыми характеристиками случайной величины называются характеристики наиболее существенных особенностей распределения - центра распределения, масштаба и формы кривой распределения, которые служат для описания и сравнения распределений. Наиболее часто используемыми в теории надежности являются математическое ожидание, дисперсия и среднее квадратическое отклонение, коэффициент вариации, асимметрия и эксцесс.
2.1 Определение математического ожидания
Математическим ожиданием  случайной величины называется постоянное число, около которого устойчиво колеблется среднее арифметическое значение случайной величины. При большой выборке среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию, которое может быть вычислено по следующей формуле:
случайной величины называется постоянное число, около которого устойчиво колеблется среднее арифметическое значение случайной величины. При большой выборке среднее арифметическое значений случайной величины сходится по вероятности к ее математическому ожиданию, которое может быть вычислено по следующей формуле:
 .
.
2.2 Определение дисперсии
Дисперсией  случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания
случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания

Дисперсия имеет размерность квадрата случайной величины, что не всегда удобно. Поэтому часто на практике используется характеристика, разменость которой совпадает с размерностью случайной величины - среднее квадратическое отклонение.
2.3 Определение среднего квадратического отклонения
Среднее квадратическое отклонение  равно квадратному корню из диперсии, взятому с положительным знаком:
равно квадратному корню из диперсии, взятому с положительным знаком:
 .
.
2.4 Определение асимметрии
Асимметрия  вычисляется по формуле
вычисляется по формуле

 |
 3 Подбор теоретического распределения для описания эмпирических данных
3 Подбор теоретического распределения для описания эмпирических данных
Случайная величина считается, исчерпывающе описанной с вероятностной точки зрения, если известна ее математическая модель - закон распределения. Из множества разработанных законов распределения наибольшее распространение для исследования эксплуатационной надежности получили экспоненциальный (показательный), нормальный (закон Гаусса) и закон Вейбулла.
Решение задачи о наилучшем подборе теоретического распределения в общем случае является неопределенным, поэтому для принятия модели описания случайной величины часто учитывают внешний вид эмпирического распределения или анализируют числовые характеристики. Например, при коэффициенте вариации V  0,3 ... 0,4 принимается нормальное распределение.
0,3 ... 0,4 принимается нормальное распределение.
В контрольной работе принимается гипотеза о принадлежности эмпирического распределения закону Вейбулла. Это объясняется тем, что этот закон является универсальным, так как при определенных значениях параметров он может превращаться в экспоненциальное (при b = 1), нормальное (при b  3,3) и другие распределения.
3,3) и другие распределения.
Распределение Вейбулла занимает центральное место при исследовании характеристик надежности машин. Этому распределению подчиняются наработки до отказа многих восстанавливаемых и невосстанавливаемых изделий, у которых отказ наступает по причине усталостного разрушения.
Непрерывная случайная величина  называется распределенной по закону Вейбулла, если ее плотность распределения имеет вид:
называется распределенной по закону Вейбулла, если ее плотность распределения имеет вид:
 при
при 
0 при  ,
,
где а – параметр масштаба,
b – параметр формы,
с – параметр сдвига.
Интегральная функция распределения записывается в виде
 .
.
Определение оценок параметров а, b и с осуществляется методом моментов, сущность которого состоит в том, что параметры функции распределения могут быть выражены через начальные и центральные моменты. По эмпирическим данным вычисляются моменты, которые затем приравниваются к теоретическим. В конечном счете решается система уравнений, связывающая параметры с моментами, и определяются оценки соответствующих параметров.
Определение оценок параметров распределения Вейбулла по совокупности статистических данных осуществляется в следующей последовательности.
По полученному значению асимметрии рь из таблицы 1 приложения Б находят оценку параметра формы b значения коэффициентов  и
и  . Значения находятся методом линейной интерполяции табличных данных.
. Значения находятся методом линейной интерполяции табличных данных.
 ,
,  ,
, 
Определяют оценку параметра масштаба а по формуле

Находим значение с по формуле

Результаты подсчета показаны в таблице 2
 № интервала № интервала
| 
| 
|
| 0,000011 | 0,08 | |
| 0,000019 | 0,19 | |
| 0,000028 | 0,36 | |
| 0,000030 | 0,58 | |
| 0,000024 | 0,78 | |
| 0,000013 | 0,92 |
С использованием полученных значений параметров a, b и c строим график плотности распределения Вейбулла.


 ,км
,км


 ,км
,км