Алфавит та рядки над алфавитом
Алфавитом V називають кінцеву непусту множину символів. Приклади: {0,1}, {a,b,c,d}. В наведених прикладах символ коми використовується як роздільник між символами. Таким чином, термін алфавит, або клас символів, позначає будь-яку кінцеву множину символів. Типовим прикладом символів можуть служити букви або алфавитно-цифрові символи. Множина {0,1} являє собою бінарний алфавит.
Конкатенацією двох символів”a” і ”b” називають операцію, наслідком якої є послідовність символів ”ab”. Це визначення розповсюджується і для послідовностей символів. Якщо позначимо операцію конкатенації символом ”+”, а отримання результату символом “→”, то : ”a”+”b” → ”ab”; ”ab”+”b2” → ”abb2”. По-іншому, якщо х и y — рядки, то конкатенація рядків х и y, що записується як ху, є рядком, сформованим шляхом дописування y до х. Наприклад, якщо x = dog, а y = house, то ху= doghouse.
Рядок над алфавитом V визначається як символ із алфавиту V або послідовність символів, яка отримана в результаті конкатенації символів або послідовності символів із алфавиту V. Таким чином, рядок над деяким алфавитом — це кінцева послідовність символів, узятих з алфавиту. У теорії мов термін речення (sentence) і слово (word) часто використаються як синоніми терміна "рядок". Довжина рядка s, звичайно позначувана як |s|, дорівнює кількості символів у рядку. Наприклад, довжина рядка banana дорівнює шести. Порожній рядок, позначуваний як ε (також, як і нульовий символ), являє собою спеціальний рядок нульової довжини або як рядок, що складається тільки з нульового символа ε.
Приклад. Хай задано алфавит V={1,2,3}. Тоді послідовності символів ”2”, ”31” та ”12331” є рядками над алфавитом V, а послідовності символів ”a”, ”341” та ”1b301” не є рядками над алфавитом V.
Хоча з функціональної і програмістської точек зору між рядками и числами є суттєва різниця, але з точки зору математики у них є певні загальні властивості.
Нехай для дійсних змінних x та y задана операція додавання „+”. Які властивості притаманні операції „+”?
а) замикання х+у – теж дійсне число. Ту ж саму властивість має операція конкатенація над рядками: в результаті операції над рядками “а”+”b”→”аb” отримуємо також рядок;
б) асоціативність: (x+y)+z = x+(y+z)=x+y+z. Для операції конкатенації над рядками теж саме (“а”+”b”)+”c”= “а”+(”b”+”c”)=“а”+”b”+”c”=”аbc”;
в) існування нульового (порожнього) елементу, тобто існує елемент і, такий що х+і=х. Для чисел це 0. Для рядків – пустий рядок, який будемо позначати символом ε (існують ще й інші позначення нейтрального елемента, наприклад, “λ”, “Ω”).
Хай V2 = V+V – множина всіх рядків довжиною 2, отриманих над V;
V3 = V2 + V – множина всіх рядків довжиною 3, отриманих над V;
Vn= Vn-1 + V – множина всіх рядків довжиною n, отриманих над V;
тоді:
Транзитивне замикання алфавиту V визначається як V+ = V ᴜ V2 ᴜ V3 ᴜ…
ᴜ Vn-1 ᴜ Vn ᴜ…
а
Рефлексивне замикання алфавиту V визначається як V* = ε ᴜ V ᴜ V2 ᴜ… = ε ᴜ V+
Деякі загальновживані терміни, що пов'язані із частинами рядків, наведені на рис. 2.3.
| Термін | Визначення | ||
| Префікс рядка s (prefix) | Рядок, отриманий видаленням нуля або декількох останніх символів рядка s; наприклад, ban є префіксом рядка banana | ||
| Суфікс рядка s (suffix) | Рядок, отриманий видаленням нуля або декількох перших символів рядка s; наприклад, nаnа є суфіксом рядка banana | ||
| Підрядок рядка s (substring) | Рядок, отриманий видаленням префікса й суфікса рядка s; наприклад, nan є підрядком рядка banana. Кожен префікс і кожен суфікс також є підрядками, але не кожен підрядок є префіксом або суфіксом. Для кожного рядка s рядки s і ε є суфіксами, префіксами й підрядками рядка s. | ||
| Правильні префікс, суфікс і підрядок рядка s | Будь-який непустий рядок х, що є відповідно префіксом, суфіксом і підрядком рядка s і не збігається з рядком s | ||
| Підпослідовність рядка s (subsequence) | Будь-який рядок, сформований видаленням нуля або декількох (не обов'язково послідовних) символів з рядка s. Так, bааа є підпослідовністю рядка banana | ||
Рис. 2.3. Терміни, що описують частини рядків
Рядки й мови
.
Термін мова (language) позначає будь-яку множину рядків над деяким фіксованим алфавитом. Таке визначення досить широке. Абстрактні мови типу Ø(порожня множина) або {ε} (множина, що містить тільки порожній рядок) також підходять під це визначення. Точно так само мовами є й множини всіх синтаксично коректних програм мовою Pascal, і всі граматично коректні речення природної мови (українською, англійської, тощо) — хоча дві останніх множини істотно складніше визначити.
Порожній рядок являє собою одиничний елемент стосовно операції конкатенації, тобто для будь-якого рядка s справедливе співвідношення sε = εs = s.
Якщо розглядати конкатенацію як операцію "множення", то можна визначити операцію "піднесення в степінь" у такий спосіб. Визначимо, що s°=ε, а для i>0 визначимо sі як sі-1s. Оскільки εs — просто s, то s1=s. Відповідно, s2=ss, s3=sss і т.д.
Операції над мовами
Є ряд важливих операцій, виконуваних над мовами. З погляду лексичного аналізу нас у першу чергу цікавлять об'єднання, конкатенація й замикання (рис. 2.4). Можна також узагальнити оператор піднесення в степень для мови, визначивши L0 як {ε}, a Lі — як Lі-1L. Таким чином, Lі являє собою L, конкатенований із самим собою і-1 раз.
| Операція | Визначення |
| Об'єднання (union) L і М – LUM | LUM ={s|s ϵ L або s ϵ M} |
| Конкатенація (concatenation) L і М – LM | LM = {st|s ϵ L й t ϵ M} |
| Замикання Кліні (Kleene closure); або ітерація L – L*. | L*=ULі , i=0, ∞ L* позначає “нуль або більше конкатенацій L” |
| Позитивне замикання (positive closure). | L+=ULі , i=1, ∞ L+ позначає "одна або більше конкатенацій L" |
Рис. 2.4. Визначення операцій над мовами
Приклад 2.2
Нехай L – множина {А, В,.. . , Z, а, b, ..., z}, а D — множина {0, 1, 2, ..., 9}. Ми можемо розглядати множини L і D подвійно. З одного боку, L являє собою алфавит, що складається з набору прописних і малих літер, a D — алфавит, що складається із цифр. З іншого боку, оскільки символ можна розглядати як рядок одиничної довжини, множини L й D являють собою кінцеві мови. От кілька прикладів нових мов, створених з L і D із застосуванням операторів, наведених на рис. 2.4.
1. LUD являє собою множину букв і цифр.
2. LD — множина рядків, що складаються з букви, за якої слідує цифра.
3. L4 — множина всіх чотирибуквених рядків.
4. L* — множина всіх рядків з букв, включаючи порожній рядок ε.
5. L(LUD)* — множина всіх рядків з букв і цифр, що починаються з букви.
6. D+ — множина всіх рядків з однієї або декількох цифр.
Регулярні вирази
У визначенні токенів важливу роль грають регулярні вирази. Кожен шаблон відповідає множини рядків, так що регулярні вирази можна розглядати як імена таких множин.
В Pascal ідентифікатор являє собою букву, за якої слідує нуль або кілька букв або цифр; отже, ідентифікатор є елементом множини, визначеного в п. 5 приклада 2.2. У цьому розділі представлений спосіб запису, іменований регулярними виразами, що дозволяє точно визначати подібні множини. За допомогою цього способу запису можна визначити ідентифікатори Pascal як
letter(letter|digit)*
Вертикальна риса означає "або", дужки використовуються для групування підвиразів, а безпосереднє сусідство letter із частиною виразу, що залишилася, означає конкатенацію.
Регулярний вираз будується з більш простих регулярних виразів із використанням набору правил. Кожний регулярний вираз r позначає або задає мову L(r). Правила визначають, яким чином з мов, заданих підвиразами r, формується L(r).
Розглянемо правила, які визначають регулярні вирази над алфавитом V.
1. ε являє собою регулярний вираз, що позначає {ε}, тобто множина, що містить порожній рядок.
2. Якщо а є символом з V, то а — регулярний вираз, що позначається {а}, тобто множина, що містить рядок а. Хоча ми використаємо ту саму запис, технічно регулярний вираз а відрізняється від рядка а й символу а. Говоримо ми про регулярний вираз, рядок або символ - стає зрозуміло з контексту.
3. Припустимо, що r и s — регулярні вирази, що позначають мови L(r) і L(s). Тоді
• (r)|(s)являє собою регулярний вираз, що позначає L(r)UL(s).
• (r)(s)— регулярний вираз, що позначає L(r)L(s).
• (r)* - регулярний вираз, що позначає (L(r))*.
• (r) — регулярний вираз, що позначає L(r).
Мова, що задається регулярним виразом, називається регулярною множиною.
Визначення регулярного виразу являє приклад рекурсивного визначення. Правила (1) і (2) формують базис визначення; використаємо термін базовий символ для ε або символу з алфавиту V, що з'являються в регулярному виразі. Правило (3) забезпечує крок індукції.
Зайві дужки в регулярному виразі можуть бути усунуті, якщо прийняти наступні угоди.
1. Унарний оператор * має вищий пріоритет і лівоасоціативен.
2. Конкатенація має другий по значимості пріоритет і лівоасоціативна.
3. | (об'єднання) має нижчий пріоритет і лівоасоціативно.
При цих угодах запис (а)|((b)*(с))еквівалентний а|b*с. Обидва вирази позначають множину рядків, які являють собою або єдиний символ а, або нуль або кілька b, за якими слідує єдиний символ с.
Приклад 2.3
Нехай V = {a,b}.
1. Регулярний вираз а|b позначає множину {а,b}.
2. Регулярний вираз (а|b)(а|b)— {аа, ab, ba, bb}, множина всіх рядків з а й b
довжини 2. Інший регулярний вираз для тієї ж множини — aa|ab|ba|bb.
3. Регулярний вираз а* — множина всіх рядків з нуля або більше а, тобто {ε, а, аа, ааа,...}.
4. Регулярний вираз (а|b)* позначає множину всіх рядків, що містять нуль
або кілька екземплярів а й b, тобто множина всіх рядків з а й b. Інший регулярний вираз для цієї множини — (а*|b*)*.
5. Регулярний вираз а|а*b — множина, що містить рядок а й всі рядки, що
складаються з нуля або декількох а, за якими слідує b.
Якщо два регулярних вирази r и s задають ту ж саму мову, то r й s називаються еквівалентними, тобто r = s. Наприклад, (а|b)=(b|а).
Є ряд алгебраїчних законів, використовуваних для перетворення регулярних виразів в еквівалентні. На рис. 2.5 наведено деякі із цих законів для регулярних виразів r, s й t.
| Аксіома | Опис |
| r|s = s|r | Оператор | комутативен |
| r | (s|t)=(r|s)|t (rǀs)ǀt | Оператор | асоціативен |
| (rs)t = r(st) | Конкатенація асоціативна |
| r(s|t) = rs|rt (s|t) r = sr|tr | Конкатенація дистрибутивна над | |
| εr = r rε = r | ε є одиничним елементом стосовно конкатенації |
| r* = (r|ε) * | Зв'язок між * й ε |
| r** = r* | Оператор * ідемпотентний |
Рис. 2.5. Алгебраїчні властивості регулярних виразів
2.2.4 Регулярні визначення
Для зручності запису регулярним виразам можна давати імена й визначати регулярні вирази з використанням цих імен так, ніби це були символи. Якщо V є алфавитом базових символів, то регулярне визначення являє собою послідовність виду
d1 → r1, d2 → r2, d3 → r3, …, dn → rn, …
де кожне di — індивідуальне ім'я, а кожне ri — регулярний вираз над символами з VU{d1,d2,...,di-1}, тобто базовими символами й уже визначеними іменами. Обмежуючи кожне ri символами з V і раніше визначеними іменами, можна побудувати регулярний вираз над V для будь-якого ri, заміняючи (можливо, неодноразово) імена регулярних виразів позначеними ними виразами. Якщо ri використає dі для якогось j ≥ i, то ri може виявитися визначене рекурсивно, і підстановка ніколи не завершиться.
Для того щоб відрізнити імена від символів, імена в регулярних виразах виділяються іншим шрифтом.
Приклад 2.4
Як говорилося раніше, множина ідентифікаторів мови Pascal являє собою множину рядків з букв і цифр, що починаються з букви. От регулярне визначення цієї множини:
letter→ A | B | ... | Z | a | b | … |z
digit→ 0 | 1 | … |9
id → letter(letter | digit)*
Приклад 2.5
Беззнакові числа в Pascal являють собою рядки типу 5280, 39.37, 6.336Е4 або 1.894Е-4. Наступне регулярне визначення забезпечує точну специфікацію цього класу рядків:
 digit → 0 | 1 | … |9
digit → 0 | 1 | … |9
digits → digit digit*
optional_fraction → .digits|ε
optional_exponent → (E(+| - | ε)digits) |ε
num → digits optional_fraction optional_exponent
Дане визначення говорить, що optional_fraction або являє собою десяткову крапку, за якою слідує одна або кілька цифр, або цей фрагмент відсутній (є порожнім рядком). У випадку наявності optional_exponentявляє собою Е, за яким слідує необов'язковий знак + або - і одна або кілька цифр. Помітимо, що за крапкою повинна випливати цифра, тобто запис 1. некоректний, на відміну від запису 1.0.
2.2.5 Скорочення
Деякі конструкції зустрічаються в регулярних виразах настільки часто, що для них уведені спеціальні скорочення.
1. Один або кілька екземплярів. Унарний постфіксний оператор + означає "один
або більше екземплярів". Якщо r - регулярний вираз, що означає мову L(r), то (r)+ являє собою регулярний вираз, що описує мову (L(r))+. Таким чином, регулярний вираз а+ описує множину всіх рядків з одного або більше а. Оператор + має той же пріоритет й асоциативність, що й оператор *.
Дві алгебраїчних тотожності r*=r+|εй r+=rr* зв'язують замикання Кліні й позитивне замикання.
2. Нуль або один примірник. Унарний постфіксний оператор ? означає "нуль або один примірник". Запис r? являє собою скорочений запис r|ε. Якщо r — регулярний вираз, то (r)? - регулярний вираз, що позначає мову L(r)U{ε}. Наприклад, використовуючи оператори + й ?, ми можемо переписати регулярний визначення для numіз приклада 2.5 як
 digit → 0 | 1 | … |9
digit → 0 | 1 | … |9
digits → digit +
optional_ffaction → (.digits)?
optional_exponent → (E(+| -)?digits)?
num → digits optional_fraction optional_exponent
3. Класи символів. Запис [abc], де a, b і с — символи алфавиту, означає регулярний вираз a | b | с. Скорочений клас символів типу [a-z]означає регулярний вираз а | b | . . . | z. З використанням класів символів можна описати ідентифікатори як рядки, задані регулярним виразом [A-Za-z] [A-Za-z0-9]*.
Нерегулярні множини
Деякі мови не можуть бути описані регулярними виразами. Для ілюстрації обмеженості описової потужності регулярних виразів наведемо приклади конструкцій мов програмування, які не можуть бути описані за допомогою регулярних виразів.
Регулярні вирази не можуть бути використані для опису збалансованих або вкладених конструкцій. Наприклад, з одного боку, множина всіх рядків зі збалансованих дужок не може бути описано регулярним виразом. З іншого боку, ця множина може бути описана за допомогою контекстно-вільної граматики.
Повторювані рядки також не можуть бути описані регулярними виразами. Множина
{wcw | w — рядок з а й b}
не може бути описано ні яким-небудь регулярним виразом, ні контекстно-вільною граматикою.
Регулярні вирази можуть використатися для опису тільки фіксованої (або невизначеної) кількості повторень даної конструкції. Два довільних числа не можуть порівнюватися в контексті регулярних виразів для з'ясування, рівні вони чи ні.
Розпізнавання токенів
У попередньому розділі ми розглянули проблему визначення (специфікації) токенів. У цьому розділі ми задамося питанням, як їх розпізнати. Тут як приклад використається мова, породжувана наступною граматикою.
Приклад 2.6
Розглянемо наступний фрагмент граматики:
stmt → if expr thenstmt
|if expr thenstmt elsestmt
expr → term relopterm
| term
term → id
| num
де нетермінали stmt, expr та term означають «оператор, «вираз» та «терм» відповідно, а термінали if, then, else, relop, id й numпороджують множини рядків, що задають наступними регулярними визначеннями:
if →if
then →then
else →else
relop → < | <= | = | <> | > | >=
id → letter (letter | digit)*
num → digit+ (. digit+)? (E(+ | -)? digit+)?
де letterй digitвизначені так само, як і раніше.
Для цього фрагмента мови лексичний аналізатор буде розпізнавати ключові слова if, then, else, а також токени, позначені relop, idй num.Для простоти вважаємо, що ключові слова зарезервовані й, таким чином, не можуть використатися як ідентифікатори. Як й у прикладі 2.5, num представляє беззнакові цілі й дійсні числа Pascal.
Припустимо також, що лексеми розділені "порожнім простором", що складається з непустих послідовностей проміжків, символів табуляцій і нового рядка. Лексичний аналізатор має відкидати ці символи шляхом порівняння рядка з регулярним визначенням ws, наведеним нижче:
ws → delim+
delim → blank | tab | newline
Якщо знаходиться відповідність ws, лексичний аналізатор не повертає токен синтаксичному аналізатору. Замість цього відбувається пошук нового токену, що випливає за проміжками, і передача його синтаксичному аналізатору.
| Регулярні вирази | ТОКЕН | атрибут-значення |
| ws | — | — |
| if | if | — |
| then | then | — |
| else | else | — |
| id | id | покажчик на запис у таблиці |
| num | num | покажчик на запис у таблиці |
| < | relop | LT |
| <= | relop | LE |
| = | relop | EQ |
| <> | relop | NE |
| > | relop | GT |
| >= | relop | GE |
Рис. 2.10. Шаблони регулярних виразів для токенів
Наша мета — побудова лексичного аналізатора, що зможе виділяти із вхідного буферу лексему для наступного токену й, використовуючи таблицю трансляції на рис. 2.10, видавати пари, що складаються з токена й атрибута-значення. Атрибут-значення для операторів відношення визначається символічними константами LT,LE,EQ,NE, GT,GE.
Діаграми переходів
Як проміжний крок при створенні лексичного аналізатора спочатку побудуємо стилізовані блок-схеми, називані діаграмами переходів (transition diagram). Діаграма переходів зображує дії, виконувані лексичним аналізатором при виклику його синтаксичним аналізатором для одержання чергового токена, як показано на рис. 2.1, Припустимо, що вхідний буфер і покажчик початку лексеми вказує на символ, що випливає за останньою знайденою лексемою. У цьому випадку ми використаємо діаграму переходів для відстеження інформації про символи, які були скановані при переміщенні покажчика forward. Щоб зробити це, ми переміщаємося при читанні символів від позиції до позиції по діаграмі переходів.
Позиції в діаграмі переходів зображуються кружками й називаються станами (states). Стани з'єднані стрілками, називаними дугами (edges). Дуги, що вихідять із стану s, мають мітки, що вказують вхідні символи, які можуть з'явитися у вхідному потоці по досягненні стану s. Мітка otherозначає появу будь-якого символу, не зазначеного іншими вихідними дугами.
У цьому розділі будемо вважати діаграми переходів детермінованими, тобто жоден символ не може бути міткою двох вихідних з одного стану дуг (далі цю умову буде послаблено).
Один зі станів має мітку start— це початковий стан діаграми переходів у момент початку розпізнавання токена. Деякі стани мають дії, виконувані при досягненні цих станів. При переході в деякий стан ми зчитуємо наступний вхідний символ й, якщо є вихідна дуга з міткою, що відповідає цьому символу, переміщаємося по ній у наступний стан. Якщо такої дуги немає, то вхідний символ некоректний, тобто відбулася помилка.
На рис. 2.11 показана діаграма переходів для шаблонів “>=” й “>”.
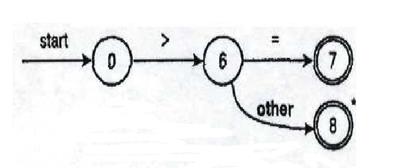
Рис. 2.11. Діаграма переходів для оператора порівняння ‘>=’ та ‘>’
Діаграма працює в такий спосіб. Робота починається в стані 0, у якому зчитується наступний символ із вхідного потоку. Дуга, позначена >, веде в стан 6, якщо цей символ — ">". У противному випадку ми не можемо розпізнати > або >=. По досягненні стану 6 зчитуємо наступний вхідний символ. Дуга, позначена як =, приводить зі стану 6 у стан 7, якщо цей символ — "=". У противному випадку по дузі otherпопадаємо в стан 8. Подвійний кружок, що зображує стан 7, показує, що це - припустимий або заключний стан, у якому знайдений токен “>=”.
Помітимо, що символ > з іншим додатковим символом приводить в інший стан, що допускає, 8. Оскільки цей інший символ не є частиною токена, він повинен бути повернутий у вхідний потік, що й зазначено зірочкою біля цього стану.
Загалом кажучи, може існувати ряд діаграм переходів, кожна з яких визначає групу токенів. Якщо при переміщенні по діаграмі переходів відбувається збій, ми повертаємо покажчик forward до того місця, де він був у стартовому стані даної діаграми, і переходимо до наступної діаграми. Оскільки покажчик на початок лексеми й покажчик forward у стартовому стані вказують на те саме місце, таке повернення здійснюється дуже просто — поверненням у позицію, що визначається покажчиком lexeme_beginning. Якщо збій відбувається у всіх діаграмах, викликається програма відновлення після помилки.
Приклад 2.7
Діаграма переходів для токена relopпоказана на рис. 2.12. Звернимо увагу на те, що рис. 2.11 являє собою частину цієї більш складної діаграми переходів.
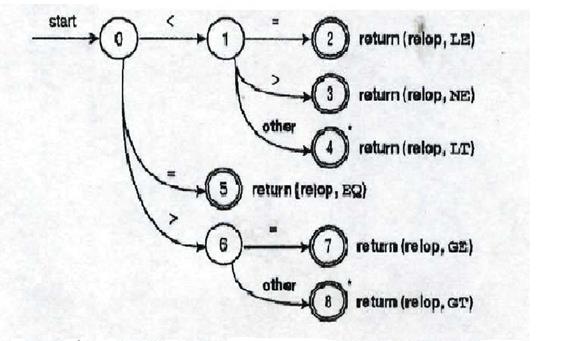
Рис. 2.12. Діаграма переходів для операторів відношення (порівняння)
Приклад 2.8
Оскільки ключові слова є не що інше, як послідовності букв, вони становлять собою виняток із правила визначення ідентифікатора як послідовністі букв і цифр, що починається з букви, є ідентифікатором. Але замість кодування виключень у діаграмі переходів можна розглядати ключові слова як спеціальні ідентифікатори. Тоді по досягненні заключного стану на рис. 2.13 виконується деякий код, що визначає, чим є лексема, що привела у цей стан, - ключовим словом або ідентифікатором.

Рис. 2. 13. Діаграма переходів для ідентифікаторів і ключових слів
Найпростіша технологія відділення ключових слів від ідентифікаторів складається у відповідній ініціалізації таблиці символів, у якій зберігається інформація про ідентифікатори. Для токенів на рис. 2.10 треба внести в таблицю символів рядка if, then й else до початку роботи із вхідним потоком. При розпізнаванні такого рядка повертається токен ключового слова. Інструкція повернення, пов'язана з припустимим станом (рис. 2.13), використає функції gettoken() і install_id() для одержання токена й атрибута-значення відповідно. Процедура install_id() має доступ до буфера, де перебуває лексема ідентифікатора. Програма перевіряє таблицю символів й, якщо лексема знайдена в ній і позначена як ключове слово, installed() повертає 0. Якщо лексема знайдена і є змінної програми, install_id()повертає покажчик на запис у таблиці символів. Якщо лексема в таблиці символів відсутня, вона вважається змінною, і функція install_id() повертає покажчик на знову створений запис у таблиці символів для цієї лексеми.
Процедура gettoken() точно так само переглядає таблицю символів у пошуках лексеми. Якщо лексема являє собою ключове слово, повертається відповідний токен; у противному випадку повертається токен id.
Помітимо, що діаграма переходів не змінюється при необхідності розпізнавання додаткового ключового слова — ми просто додаємо нове ключове слово в таблицю символів при ініціалізації.
Технологія розміщення ключових слів у таблиці символів відіграє важливу роль при створенні лексичного аналізатора вручну. Без цього в лексичному аналізаторі для типової мови програмування кількість станів дорівнює декільком сотням, у той час як при використанні описаного способу звичайно вистачає менш сотні станів.

Рис. 2.14.Діаграми переходів для беззнакових чисел в Pascal
Приклад 2.9
Число проблем зростає при побудові розпізнавальника беззнакових чисел, що задають регулярним виразом
num → digit* (. digit+)? (E(+ | -)? digit+)?
Звернемо увагу на те, що визначення має вигляд digits fraction? exponent?, де fractionй exponent— необов'язкові частини.
Лексема для даного токена повинна бути максимально можливої довжини (правило пошуку лексеми найбільшої довжини — загальноприйняте правило роботи лексичного аналізатора, що дозволяє уникнути багатьох неприємностей). Наприклад, лексичний аналізатор не повинен зупинятися після того, як зустріне 12 або навіть 12.3, якщо уведено число 12.3Е4. Починаючи зі станів 25, 20 й 12 на рис. 2.14, що допускають стани при одержанні у вхідному потоці рядка 12.3Е4, за яким слідує нецифровий символ, досягаються після зчитування 12, 12.3 й 12.3Е4 відповідно. Діаграми переходів зі стартовими станами 25, 20 й 12 описують відповідно digits, digits fractionй digits fraction? exponent,так що випробовувати їх треба у зворотному порядку — 12, 20, 25.
По досягненні кожного з припустимих станів 19, 24 й 27 відбувається виклик процедури install_num(), що вносить лексему в таблицю чисел і повертає покажчик на створений запис. Лексичний аналізатор повертає токен num із цим
покажчиком як лексичне значення.
Інформація про мову, що втримується поза регулярними визначеннями токенів, може використатися для точної вказівки помилок у вхідному тексті. Наприклад, при уведенні 1,<х збій відбудеться в станах 14 й 22 на рис. 2.14 при одержанні чергового вхідного символу "<". Замість того, щоб повернути число 1, можна повідомити про помилку й продовжити роботу так, ніби був уведений рядок 1.0<х. Таким чином, знання особливостей мови забезпечує можливість відновлення при деяких помилках, які інакше привели б до аварійного завершення трансляції.
Є ряд способів уникнути зайвих перевірок у діаграмах переходів на рис. 2.14. Один з підходів полягає в тому, щоб переписати діаграми переходів, об'єднавши їх в одну (що взагалі ж є нетривіальним завданням). Інший шлях - змінити реакцію на помилки в процесі роботи з діаграмою. Підхід, розглянутий пізніше в цій главі, дозволяє пройти по ряду станів, що допускають, повертаючись назад до останнього пройденого припустимого стану перед збоєм.
Приклад 2.10
Послідовність діаграм переходів для всіх токенів із приклада 2.6 здійснюється при об'єднанні діаграм переходів, зображених на рис. 2.12-2.14. Стартові стани з меншими номерами випробовуються перед станами з більшими номерами.
У цьому випадку залишається тільки проблема, пов'язана із проміжками. Обробка регулярного визначення ws, що представляє проміжки, відрізняється від обробки шаблонів тим, що синтаксичному аналізатору не повертається який-небудь токен. Діаграма переходів, що розпізнає проміжки, виглядає в такий спосіб.

|
При цьому по досягненні стану, що допускає, синтаксичному аналізатору не повертається ніяке значення; ми просто повертаємося до стартового стану першої діаграми переходів для пошуку іншого шаблона.
По можливості варто починати перегляд із токенів, що часто зустрічаються,
оскільки робота з деякою діаграмою переходів починається тільки після завершення
роботи з її попередниками. У зв’язу з тим, що проміжки зустрічаються досить часто, розміщення діаграми переходів для проміжків перед іншими повинне підвищити загальну ефективність.