АЛГОРИТМ РАСЧЛЕНЕНИЯ БЕНДЕРСА ДЛЯ ЧАСТИЧНО-ЦЕЛОЧИСЛЕННЫХ ЗАДАЧ ЛИНЕНОГО ПРОГРАММИРОВАНИЯ

ЗАДАЧА О РАЗМЕЩЕНИИ ПРОМЫШЛЕННЫХ ПРЕДПРИЯТИЙ

Целью работы является изучение метода расчленения Бендерса для решения задач частично-целочисленного программирования и приобретения практических навыков использования этого метода при решении конкретных задач, на примере решения задачи о размещении складов (промышленных предприятий).

ЗАДАЧИ ЧАСТИЧНО-ЦЕЛОЧИСЛЕННОГО ПРОГРАММИРОВАНИЯ

Математическая формулировка задачи частично-целочисленного программирования обычно записывается в следующем виде:

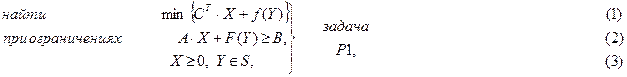где Х – n-мерный вектор; А - матрица размерности (m·n); С – n-мерный вектор; f(Y) – функция p-мерного вектора Y; F(Y) –вектор – функция; S – произвольное подмножество E^Р;T – обозначение операции транспонирования. Если зафиксировать значение Y, то задача (1)-(3) переходит в задачу линейного программирования.

Многие важные в практическом отношении задачи могут быть приведены к виду (1)-(3). Если S – множество векторов с неотрицательными целочисленными компонентами, а F и f – линейны, то (1)-(3) – представляет собой задачу частично-целочисленного линейного программирования (ЛП). Существенным для этих задач является аддитивность вхождения функции от Y в ограничения и целевую функцию.

Существуют множество методов решения задач рассматриваемого класса. Наиболее подходящим и эффективным является алгоритм расчленения Бендерса [1]. В соответствии с этим алгоритмом задача (1)-(3) решается в следующей последовательности:

а) фиксируется некоторое значение Y^*ϵ S и решается задача:

(4)

б) на основе решения двойственной задачи для (4) определяется возможность улучшения решения, полученного на первом шаге, и находится новое значение вектора Y. Таким образом, полностью используется преимущество частичной линейной задачи, что особенно важно, когда матрица A имеет специальную структуру (например, блочно-диагональную или транспортного типа). В этом случае задача (4) сравнительно легко решается. Эти преимущества не реализуются при использовании алгоритмов, в которых X и Y изменяются одновременно.

АЛГОРИТМ РАСЧЛЕНЕНИЯ БЕНДЕРСА ДЛЯ ЧАСТИЧНО-ЦЕЛОЧИСЛЕННЫХ ЗАДАЧ ЛИНЕНОГО ПРОГРАММИРОВАНИЯ

Необходимо решить задачу (1)-(3). Поскольку она линейна по X при фиксированных значениях Y, естественно попытаться решить ее путем решения линейной задачи относительно X при фиксированных Y и определения «лучшего» значения Y и.т.д. Конечно, могут рассматриваться только такие значения Y, для которых существуют X, удовлетворяющие полученным линейным ограничениям, т.е. Y должны лежать в множестве:

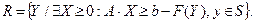(5) По лемме Фаркаша [2] множество R мы можем записать в другом виде:

. (6)

Если R пусто, то исходная задача (1)-(3) не имеет допустимого решения. Предполагая R непустым, перепишем задачу (1)-(3) в виде:

(7)

Для фиксированного Y внутренняя минимизация в (7) есть задача линейного программирования. Запишем ее вместе с двойственной к ней:

прямая (8)

двойственная (9)

Если Y ϵ R, то прямая задача допустима и в силу теоремы двойственности имеем

(10)

Где значение максимума принимается равным -∞, если двойственная задача недопустима. Соотношение (10) суммирует утверждение, что если прямая задача ЛП имеет неограниченное решение, то двойственная задача недопустима; в то время как если обе задачи допустимы, то они имеют конечное оптимальное решение с равными значениями целевых функций.

Подставляя (10) в (7) приходим к новой форме задачи (1)-(3):

. (11)

Рассмотрим множество ограничений двойственной задачи

(12)

Здесь ограничения (12) не зависят от y. Если P пусто, то двойственная задача (9) имеет неограниченное решение, также как и прямая задача (8). Если Р не пусто, то внутренний максимум в (11) достигается в одной из крайних точек Р или стремится к ∞ при движении по крайнему лучу Р. В последнем случае прямая задача (7) недопустима, что противоречит нашим исходным предположениям, так что мы можем ограничиться рассмотрением только крайних точек Р. Таких точек имеется конечное число. Обозначим их- .Таким образом, задача (11) может быть переписана в виде:

(13)

Задачу (13), по другому, можно переписать в виде

Используя определение R, данное ограничениями (6), мы можем переписать (14)-(16) и получить новую задачу Р2:

Из вышеизложенного ясна связь между задачами Р1 и Р2 – они эквивалентны между собой.

Таким образом, решение исходной задачи (1)-(3) мы свели к решению задачи (17)-(20). К сожалению, решение задачи Р2 затруднительно в силу того, что для каждой крайней точки и крайнего луча множества Р имеется по одному ограничению, так что их общее число даже для задачи умеренной размерности может быть большим. Однако лишь малая часть ограничений является связующей в оптимальном решении. Поэтому здесь естественно применять релаксационный метод. При этом можно начать с учета только малого числа ограничений и решать модифицированные таким образом задачи Р2, которые в дальнейшем будем обозначать МР2. Относительно просто проверить, удовлетворяет ли решение остающимся ограничениям. Если это так, то решение оптимально, поскольку целевая функция минимизируется на множестве, содержащем G = [ (Z, Y)/(Z,Y) удовлетворяет (18)-(20)]. Если это не так, то добавляются ограничения, которые не удовлетворялись на текущем решении, и задача решается заново. Результирующий алгоритм состоит в итеративном решении двух задач. Первая задача есть задача МР2, в которую последовательно добавляются ограничения. Вторая задача есть двойственная линейная задача (9) или прямая (8), которая служит для испытания на оптимальность решений МР2 и, если необходимо, дает новые ограничения.

В качестве критерия достижения оптимума можно использовать следующий: точка (Z⁰, Y⁰)- оптимальная для МР2 является оптимальной для задачи Р2, тогда и только тогда, когда выполняется соотношение:

При выполнении этого критерия оптимальная точка найдена и решение задачи на этом заканчивается. При невыполнении его в задачу МР2 добавляется новое ограничение и снова решаются задачи МР2, (9), (8) и так до тех пор, пока критерий не будет выполнен или в задачу МР2 не будут добавлены все ограничения сгенерированные в (9), и поскольку этих ограничений конечное число, решение задачи закончится за конечное число шагов.

Процедура релаксации требует вогнутости f(y) или F(y). При отсутствии этого условия необходимо выполнение условий замкнутости и ограниченности S, а также, чтобы f(y) и компоненты F(y) являлись непрерывными на S.

Эти условия удовлетворяются в большинстве приложений и позволяют избежать трудностей рассмотрения задач, имеющих неограниченное решение. Если S не является ограниченным, то могут быть добавлены покомпонентные ограничения сверху и снизу на Y. При этом границы могут быть взяты столь большими, что они заведомо включают оптимальное решение, либо таковы, что любое решение, превышающее эти ограничения, не может быть реально интегрировано.

Краткое изложение алгоритма метода расчленения Бендерса:

1. Процедура начинается с решения проблемы МР2, в которой только несколько (или ни одного) ограничения вида (18), (19).

2. Если решение МР2 недопустимо, то недопустимы Р2 и Р1. В противном случае мы получаем конечное оптимальное решение (Z⁰, Y⁰), либо информацию о том, что решение является неограниченным. Если Z⁰ = -∞, то принимаем в качестве Y⁰ произвольный элемент S и переходим к пункту 3.

3. Решается двойственная линейная задача (9) или прямая (8), если она допустима. Если двойственная задача недопустима, то исходная задача Р1 имеет неограниченное решение. Если двойственная задача – неограниченная, то переходим к пункту 6.

4. Если оптимальное значение целевой на шаге 3 равно Z⁰ – f(Y⁰), то решение (Z⁰, Y⁰) является решением Р2. Если X⁰ – решение (8), то (X⁰, Y⁰) –решение (1)-(3).

5. Если на шаге 3 не проходит критерий оптимальности и двойственная задача (9) имеет конечное – оптимальное решение u⁰, то так что текущее решение МР2 не удовлетворяет ограничению Тогда это ограничение добавляется к МР2 и осуществляется возврат к пункту 2.

6. Если двойственная (9) имеет неограниченное решение, то симплекс-метод позволяет найти луч V⁰ и точку u⁰ такие, что целевая функция задачи стремится к +∞ на луче Неравенство (24) удовлетворяется, так что Y⁰ не удовлетворяет ограничению Добавим это ограничение к МР2. Если также имеет место для крайней точки u⁰ , указанной в (23), то добавим ограничение вида (22) к МР2. После этого возвращаемся к пункту 2.

Конечная сходимость алгоритма следует из конечности числа ограничений в задаче Р2.

Далее ⇒