Оценивание неизвестных параметров распределений

УДК 519.2(075)

ББК 22.171

Инновационная образовательная программа "Развитие центра компетенции и подготовка специалистов мирового уровня в области аэрокосмических и геоинформационных технологий"

Автор: Э.И. Коломиец

Рецензенты: д-р физ.-мат.наук, проф. А.И. Жданов;

д-р физ.-мат.наук, проф. С.Я.Шатских.

Моделирование и статистический анализ случайных данных:учебное пособие / [Э.И.Коломиец]. – Самара: Изд-во Самар. гос. аэрокосм. ун-та, 2007. – 80 с. : ил.

Учебное пособие содержит полное методическое обеспечение всех видов учебных занятий по разделу «Математическая статистика» курсов «Теория вероятностей и математическая статистика» и «Основы теории стохастических процессов», изучаемых студентами направлений «Прикладная математика и информатика» и «Прикладные математика и физика» соответственно. В состав учебного пособия входят: краткие теоретические сведения, методические указания по проведению практических занятий, варианты индивидуального задания для расчетно-графической работы или для курсового проекта (в зависимости от действующего учебного плана) и методические указания по его выполнению с использованием универсальных пакетов MCAD и MATLAB. Учебное пособие предназначено для получения студентами практических навыков при статистическом анализе случайных данных и для совершенствования форм самостоятельной работы.

УДК 517.2(075)

ББК 22.171

©Коломиец Э.И., 2007

аэрокосмический университет, 2007

СОДЕРЖАНИЕ

Введение…………………………………………………………………………..

1. Теоретические сведения.

1.1. Выборка. Эмпирическая функция распределения.

Гистограмма. Выборочные числовые характеристики………………..

1.2. Оценивание неизвестных параметров распределений…………………….

1.2.1. Точечные оценки. Методы нахождения точечных оценок………

1.2.2. Интервальные оценки………………………………………………

1.3. Проверка статистических гипотез…………………………………………

1.3.1. Проверка гипотезы о виде распределения…………………………

1.4. Изучение зависимости между случайными величинами………………….

1.4.1. Оценка коэффициента корреляции…………………………………

1.4.2. Проверка гипотезы о независимости………………………………..

1.4.3. Эмпирические уравнения регрессии……………………………….

1.5. Моделирование случайных величин и векторов………………………….

1.5.1. Моделирование непрерывных случайных величин………………..

1.5.2. Моделирование гауссовского случайного вектора…………………

2. Практические занятия.

2.1. Первичная обработка статистических данных.

2.2. Точечные оценки неизвестных параметров.

2.3. Интервальные оценки неизвестных параметров.

2.4. Проверка статистических гипотез.

3. Индивидуальное задание «Моделирование и статистический

анализ случайных данных»……………………………………………………

3.1. Содержание задания.

3.2. Исходные данные к заданию.

3.3. Методические указания по выполнению задания.

3.4. Требования к оформлению пояснительной записки.

Литература

Приложение 1. Варианты индивидуальных заданий.

Приложение 2. Нормальное распределение.

Приложение 3. Распределение Стьюдента .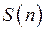

Приложение 4. Распределение хи-квадрат .

Приложение 5. Образец оформления титульного листа.

ВВЕДЕНИЕ

Тезис о том, что «критерий истины есть практика» имеет самое непосредственное отношение к математической статистике,- науке, занимающейся анализом случайных данных. Именно эта наука изучает методы (в рамках точных математических моделей), которые позволяют отвечать на вопрос, соответствует ли практика, представленная в виде результатов эксперимента, данному гипотетическому представлению о природе явления или нет. При этом имеются в виду не эксперименты, которые позволяют делать однозначные, детерминированные выводы о рассматриваемых явлениях, а эксперименты, результатами которых являются случайные события. С развитием науки задач такого рода становится все больше и больше, поскольку с увеличением точности экспериментов становится все труднее избежать «случайного фактора», связанного с различными помехами и ограниченностью наших измерительных и вычислительных возможностей. Вот почему за последнее время статистические методы, проникнув в самые разнообразные области науки и техники, стали широко использоваться при анализе и обработке опытных данных. Этот процесс находит отражение и в обучении по направлениям «Прикладная математика и информатика» и «Информационные технологии», в соответствии с учебными планами которых существенное время отводится на изучение дисциплин вероятностного цикла, что обусловлено неуклонным возрастанием их практической значимости.

Цель данного учебного пособия – привить студентам практические навыки обработки экспериментальных случайных данных с использованием теоретических методов классической математической статистики и современных программных пакетов со встроенными статистическими функциями, а также предоставить студентам методическую поддержку при самостоятельной работе.

Учебное пособие содержит полное методическое обеспечение всех видов учебных занятий по разделу «Математическая статистика» и в его состав входят: краткие теоретические сведения, методические указания по проведению практических занятий, варианты индивидуального задания для расчетно-графической работы или для курсового проекта (в зависимости от действующего учебного плана) и методические указания по его выполнению, примеры выполнения задания с использованием универсальных пакетов MCAD и MATLAB.

ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ

1.1. Выборка. Эмпирическая функция распределения. Гистограмма.
Выборочные числовые характеристики

В математической статистике имеют дело со стохастическими экспериментами, состоящими в проведении повторных независимых наблюдений над некоторой случайной величиной , имеющей неизвестное распределение вероятностей, т.е. неизвестную функцию распределения
. В этом случае множество всех возможных значений наблюдаемой случайной величины называют генеральной совокупностью, имеющей функцию распределения . Числа , являющиеся результатом независимых наблюдений над случайной величиной , называют выборкой из генеральной совокупности или выборочными (статистическими) данными. Число наблюдений называется объемомвыборки.

Основная задача математической статистики состоит в том, как по выборке , извлекая из нее максимум информации, сделать обоснованные выводы относительно вероятностных характеристик наблюдаемой случайной величины .

Замечание: Выборка является исходной информацией для статистического анализа и принятия решений о неизвестных вероятностных характеристиках наблюдаемой случайной величины . Однако на основе конкретной выборки обосновать качество статистических выводов принципиально невозможно. Для этого на выборку следует смотреть априорно как на случайный вектор , координаты которого являются независимыми, распределенными так же как и , случайными величинами, и который еще не принял конкретного значения в результате эксперимента. Переход от выборки конкретной к выборке случайной будет неоднократно использоваться далее при решении теоретических вопросов и задач для получения выводов, справедливых для любой выборки из генеральной совокупности.

В зависимости от дальнейших целей существует несколько способов представления статистических данных. Простейший из них - в виде статистического ряда:

Номер наблюдения	1 2 …
Результат наблюдения	…

Если среди выборочных значений имеются совпадающие, то статистический ряд удобнее записывать в виде таблицы, называемой таблицей частот:

Выборочные значения			…
Частоты			…
Относительные частоты			…

где - различные значения среди ; - частота значения ; - относительная частота значения . Очевидно, что . Поэтому совокупность пар называют эмпирическим законом распределения.

Выборочные значения , упорядоченные по возрастанию, носят название вариационного ряда:

где , .

Величина называется размахом выборки.

Эмпирической функцией распределения, соответствующей выборке
, называется функция

где - индикатор множества , а - число выборочных значений, не превосходящих .

Для заданной выборки эмпирическая функция распределения обладает всеми свойствами обычной функции распределения: принимает значения между 0 и 1, является неубывающей и непрерывной слева. График имеет ступенчатый вид, причем:

если все значения различны, то

при , , ;

если - различные значения среди , то

Принципиальное отличие эмпирической функции распределения от обычной функции распределения состоит в том, что она может изменяться от выборки к выборке и притом случайным образом. Важнейшим свойством эмпирической функции распределения как случайной функции (см. замечание выше) является то, что она для любого при увеличении объема выборки сближается (в смысле сходимости по вероятности) с истинной функцией распределения . Поэтому говорят, что эмпирическая функция распределения является статистическим аналогом (оценкой) неизвестной функции распределения , которую называют при этом теоретической.

Если - выборка объема из генеральной совокупности, имеющей непрерывное распределение с неизвестной плотностью вероятностей , то для получения статистического аналога следует предварительно произвести группировку данных. Она состоит в следующем:

1. По данной выборке строят вариационный ряд

2. Промежуток разбивают точками на непересекающихся интервалов (на практике ).

3. Подсчитывают частоты попадания выборочных значений в -ый интервал .

4. Полученную информацию заносят в следующую таблицу, которую называют интервальным статистическим рядом:

Интервалы			…
Частоты			…
Относительные частоты			…

Очевидно, что . Поэтому совокупность пар , где - середина интервала , называют эмпирическим законом распределения, полученным по сгруппированным данным.

Далее в прямоугольной системе координат на каждом интервале как на основании длиной строят прямоугольник с высотой . Получаемую при этом ступенчатую фигуру называют гистограммой.

Поскольку при больших в соответствии с теоремой Бернулли , где - истинная вероятность попадания случайной величины в интервал , а , то справедливо приближенное равенство . Поэтому верхняя граница гистограммы является статистическим аналогом (оценкой) неизвестной плотности вероятностей .

Ломаная с вершинами в точках называется полигоном частот и для гладких плотностей является более точной оценкой, чем гистограмма. Пример гистограммы и полигона частот приведен на рис.1.

На практике при группировке данных обычно берут интервалы одинаковой длины соnst, а число интервалов группировки определяют с помощью так называемого правила Стургерса, согласно которому полагается .

Рис. 1. Гистограмма и полигон частот

Пусть - выборка из генеральной совокупности, имеющей функцию распределения . Аналогично тому, как теоретической функции распределения ставят в соответствие эмпирическую функцию распределения , любой теоретической характеристике можно поставить в соответствие ее статистический аналог - выборочную (эмпирическую) числовую характеристику g*, определяемую как среднее арифметическое значений функции g(х) для элементов выборки :

В частности, выборочный начальный момент -го порядка есть величина

При k = 1 величину называют выборочным средним и обозначают :

Выборочный центральный момент -го порядка есть величина

При величину называют выборочной дисперсией и обозначают :

Между выборочными начальными и выборочными центральными моментами сохраняются те же соотношения, что и между теоретическими. Например, справедливо равенство

являющееся аналогом известного равенства

Являясь для заданной выборки числами, в общем случае выборочные числовые характеристики являются случайными величинами и обозначаются соответствующими заглавными буквами:

; ; ;

; .

В связи с этим можно ставить вопрос о нахождении закона распределения выборочных числовых характеристик и их числовых характеристиках.

Располагая только сгруппированными данными, можно определить аналог эмпирической функции распределения следующим образом:

Для вычисления выборочных моментов -го порядка по сгруппированным данным используются формулы:

В частности, выборочное среднее и выборочная дисперсия по сгруппированным данным определяются с помощью формул:

Оценивание неизвестных параметров распределений

Пусть имеется выборка , представляющая собой результат независимых наблюдений над некоторой случайной величиной , и предположим, что тип распределения генеральной совокупности известен, но зависит от неизвестного параметра: . В общем случае задача оценивания формулируется так: используя информацию, доставляемую выборкой, сделать статистические выводы об истинном значении неизвестного параметра , т.е. оценить параметр .

Различают точечные и интервальные оценки неизвестных параметров.

Далее ⇒