Общее представление о вторичной обработке
Вторичная обработказаключается главным образом в статистическом анализе итогов первичной обработки. Уже табулирование и построение графиков, строго говоря, тоже есть статистическая обработка, которая в совокупности с вычислением мер центральной тенденции и разброса включается в один из разделов статистики, а именно в описательную статистику. Другой раздел статистики — индуктивная статистика [19]— осуществляет проверку соответствия данных выборки всей популяции, т. е. решает проблему репрезентативности результатов и возможности перехода от частного знания к общему [10, 34, 41, 42]. Третий большой раздел — корреляционная статистика — выявляет связи между явлениями. В целом же надо понимать, что «статистика — это не математика, а, прежде всего, способ мышления, и для ее применения нужно лишь иметь немного здравого смысла и знать основы математики» [19, т. 2, с. 277].
Статистический анализ всей совокупности полученных в исследовании данных дает возможность охарактеризовать ее в предельно сжатом виде, поскольку позволяет ответить на три главных вопроса: 1)какое значение наиболее характерно для выборки?; 2) велик ли разброс данных относительно этого характерного значения, т. е. какова «размытость» данных?; 3) существует ли взаимосвязь между отдельными данными в имеющейся совокупности и каковы характер и сила этих связей? Ответами на эти вопросы служат некоторые статистические показатели исследуемой выборки. Для решения первого вопроса вычисляются меры центральной тенденции (или локализации), второго — меры изменчивости (или рассеивания, разброса), третьего — меры связи (или корреляции). Эти статистические показатели приложимы к количественным данным (порядковым, интервальным, пропорциональным).
Меры центральной тенденции(м. ц. т.) — это величины, вокруг которых группируются остальные данные. Эти величины являются как бы обобщающими всю выборку показателями, что, во-первых, позволяет по ним судить обо всей выборке, а во-вторых, дает возможность сравнивать разные выборки, разные серии между собой. К мерам центральной тенденции относятся: среднее арифметическое, медиана, мода, среднее геометрическое, среднее гармоническое.
Среднее арифметическое (М) —это результат деления суммы всех значений (X) на их количество (N): М = ЕХ / N.
Медиана (Me) — это значение, выше и ниже которого количество отличающихся значений одинаково, т. е. это центральное значение в последовательном ряду данных.
Примеры: 3,5,7,9,11,13,15; Me = 9.
3,5,7,9, 11, 13, 15, 17; Me = 10. [20]
Из примеров ясно, что медиана не обязательно должна совпадать с имеющимся замером, это точка на шкале. Совпадение происходит в случае нечетного числа значений (ответов) на шкале, несовпадение — при четном их числе.
Мода (Мо) — это значение, наиболее часто встречающееся в выборке, т. е. значение с наибольшей частотой.
Пример: 2, 6, 6, 8, 9, 9, 9, 10; Мо = 9.
Если всё значения в группе встречаются одинаково часто, то считается, что моды нет (например: 1, 1, 5, 5, 8, 8). Если два соседних значения имеют одинаковую частоту и они больше частоты любого другого значения, мода есть среднее этих двух значений (например: 1, 2, 2, 2, 4, 4, 4, 5, 5, 7; Мо = 3). Если то же самое относится к двум несмежным значениям, то существует две моды, а группа оценок является бимодальной (например: 0, 1, 1, 1, 2, 3, 4, 4, 4, 7; Мо = 1 и 4).
Обычно среднее арифметическое применяется при стремлении к наибольшей точности и когда впоследствии нужно будет вычислять стандартное отклонение. Медиана — когда в серии есть «нетипичные» данные, резко влияющие на среднее (например: 1, 3, 5, 7, 9, 26, 13). Мода — когда не нужна высокая точность, но важна быстрота определения м. ц. т.
Меры изменчивости (рассеивания, разброса)— это статистические показатели, характеризующие различия между отдельными значениями выборки. Они позволяют судить о степени однородности полученного множества, о его компактности, а косвенно и о надежности полученных данных и вытекающих из них результатов. Наиболее используемые в исследованиях показатели: размах, среднее отклонение, дисперсия, стандартное отклонение, полуквартилъное отклонение.
Размах (Р) —это интервал между максимальным и минимальным значениями признака. Определяется легко и быстро, но чувствителен к случайностям, особенно при малом числе данных.
Примеры: (0, 2, 3, 5, 8; Р = 8); (-0.2, 1.0, 1.4, 2.0; Р - 2,2).
Среднее отклонение (МД) — это среднеарифметическое разницы (по абсолютной величине) между каждым значением в выборке и ее средним: МД = Id / N, где: d = |Х-М|; М — среднее выборки; X — конкретное значение; N — число значений. [21]
Множество всех конкретных отклонений от среднего характеризует изменчивость данных, но, если их не взять по абсолютной величине, то их сумма будет равна нулю, и мы не получим информации об их изменчивости. МД показывает степень скученности данных вокруг среднего. Кстати, иногда при определении этой характеристики выборки вместо среднего (М) берут иные меры центральной тенденции — моду или медиану.
Дисперсия (Д) (от лат. dispersus — рассыпанный). Другой путь измерения степени скученности данных предполагает избегание нулевой суммы конкретных разниц (d = Х-М) не через их абсолютные величины, а через их возведение в квадрат. При этом получают так называемую дисперсию:
Д = Σd2 / N — для больших выборок (N > 30);
Д = Σd2 / (N-1) — для малых выборок (N < 30).
Стандартное отклонение (δ). Из-за возведения в квадрат отдельных отклонений d при вычислении дисперсии полученная величина оказывается далекой от первоначальных отклонений и потому не дает о них наглядного представления. Чтобы этого избежать и получить характеристику, сопоставимую со средним отклонением, проделывают обратную математическую операцию — из дисперсии извлекают квадратный корень. Его положительное значение и принимается за меру изменчивости, именуемую среднеквадратическим или стандартным отклонением:
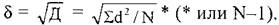
МД, Д и d применимы для интервальных и пропорционных данных. Для порядковых данных обычно в качестве меры изменчивости берут полуквартильное отклонение (Q), именуемое еще полуквартильным коэффициентом или полумеждуквартильным размахом. Вычисляется этот показатель следующим образом. Вся область распределения данных делится на четыре равные части. Если отсчитывать наблюдения, начиная от минимальной величины на измерительной шкале (на графиках, полигонах, гистограммах отсчет обычно ведется слева направо), то первая четверть шкалы называется первым квартилем, а точка, отделяющая его от остальной части шкалы, обозначается символом Q,. Вторые 25% распределения — второй квартиль, а соответствующая точка на шкале — Q2. Между третьей и четвертой четвертя-[22]ми распределения расположена точка Q,. Полу квартальный коэффициент определяется как половина интервала между первым и третьим квартилями: Q = (Q.-Q,) / 2.
Понятно, что при симметричном распределении точка Q0 совпадет с медианой (а следовательно, и со средним), и тогда можно вычислить коэффициент Q для характеристики разброса данных относительно середины распределения. При несимметричном распределении этого недостаточно. И тогда дополнительно вычисляют коэффициенты для левого и правого участков: Qлев= (Q2-Q,) / 2; Qправ= (Q, — Q2) / 2.
Меры связи
Предыдущие показатели, именуемые статистиками, характеризуют совокупность данных по одному какому-либо признаку. Этот изменяющийся признак называют переменной величиной или просто «переменной». Меры связи же выявляют соотношения между двумя переменными или между двумя выборками. Эти связи, или корреляции (от лат. correlatio — 'соотношение, взаимосвязь') определяют через вычисление коэффициентов корреляции (R), если переменные находятся в линейной зависимости между собой. Но наличие корреляции не означает, что между переменными существует причинная (или функциональная) связь. Функциональная зависимость— это частный случай корреляции. Даже если связь причинна, корреляционные показатели не могут указать, какая из двух переменных причина, а какая — следствие. Кроме того, любая обнаруженная связь, как правило, существует благодаря и другим переменным, а не только двум рассматриваемым. К тому же взаимосвязи признаков столь сложны, что их обусловленность одной причиной вряд ли состоятельна, они детерминированы множеством причин.
Виды корреляции:
I. По тесноте связи:
1) Полная (совершенная): R = 1. Констатируется обязательная взаимозависимость между переменными. Здесь уже можно говорить о функциональной зависимости.
2) связь не выявлена: R = 0. [23]
3) Частичная: 0<R<1. Меньше 0,2 —очень слабая связь; (0,2-0,4) — корреляция явно есть, но невысокая; (0,4-0,6) — явно выраженная корреляция; (0,6-0,8) — высокая корреляция; больше 0,8 — очень высокая.
Встречаются и другие градации оценок тесноты связи [61].
Кроме того, при оценке тесноты связи используют так называемую «частную» классификацию корреляционных связей. Эта классификация ориентирована не на абсолютную величину коэффициентов корреляции, а на уровень значимости этой величины при определенном объеме выборки. Эта классификация применяется при статистической оценке гипотез. Тогда чем больше выборка, тем меньшее значение коэффициента корреляции может быть принято для признания достоверности связей. А для малых выборок даже абсолютно большое значение R может оказаться недостоверным [75].
II. По направленности:
1) Положительная (прямая);
Коэффициент R со знаком «плюс» означает прямую зависимость: при увеличении значения одной переменной наблюдается увеличение другой.
2) Отрицательная (обратная).
Коэффициент R со знаком «минус» означает обратную зависимость: увеличение значения одной переменной влечет уменьшение другой.
III. По форме:
1) Прямолинейная.
При такой связи равномерным изменениям одной переменной соответствуют равномерные изменения другой. Если говорить не только о корреляциях, но и о функциональных зависимостях, то такие формы зависимости называют пропорциональными.
2) Криволинейная.
Это связь, при которой равномерное изменение одного признака сочетается с неравномерным изменением другого.
Формулы коэффициента корреляции:
При сравнении порядковых данных применяется коэффициент ранговой корреляции по Ч. Спирмену (ρ): ρ = 6Σd2 / N (N2 — 1), где: d — разность рангов (порядковых мест) двух величин, N — число сравниваемых пар величин двух переменных (X и Y). [24]
При сравнении метрических данных используется коэффициент корреляции произведений по К. Пирсону (r): r = Σ ху / Nσxσy
где: х — отклонение отдельного значения X от среднего выборки (Мх), у — то же для Y, Ох — стандартное отклонение для X, а — то же для Y, N — число пар значений X и Y.
Внедрение в научные исследования вычислительной техники позволяет быстро и точно определять любые количественные характеристики любых массивов данных. Разработаны различные программы для ЭВМ, по которым можно проводить соответствующий статистический анализ практически любых выборок. Из массы статистических приемов наибольшее распространение получили следующие: 1) комплексное вычисление статистик; 2) корреляционный анализ; 3) дисперсионный анализ; 4) регрессионный анализ; 5) факторный анализ; 6) таксономический (кластерный) анализ; 7) шкалирование.