СОБСТВЕННЫЕ ФУНКЦИИ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ

МАТЕМАТИЧЕСКИЙ АППАРАТ КВАНТОВОЙ МЕХАНИКИ

 

В квантовой механике каждой динамической переменной (координате, импульсу, энергии и т.д.) ставится в соответствие линейный самосопряженный оператор. Оператором 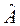наз. правило или закон, согласно которому функции 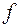, из некоторого класса функций, ставится в соответствие другая функция φ.

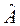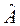Операторы обозначаются символом ^ , например, , , и т.д. Говорят, что оператор действует на функцию f или оператор 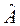переводит функцию

f в φ :

(1)

Например, = ; .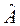

Действуя оператором на функцию, получим:

, .

Оператор определен на некотором классе функций. Оператор считается заданным, если указано не только правило, с помощью которого он преобразует одну функцию в другую, но и то множество функций, на которые действует этот оператор. Например, оператор дифференцирования определен на классе дифференцируемых функций.

Сумма или разность операторов означает

В общем случае , но если последовательность действия операторов не имеет значения, т.е. , то говорят, что эти операторы коммутируют или эти операторы коммутативны. Если операторы не коммутативны. Кроме коммутативных и некоммутативных операторов существуют антикоммутативные операторы: .

Произведение 2-х одинаковых операторов: , n раз : .

В квантовой механике большую роль играют линейные самосопряженные (эрмитовы) операторы. Свойство линейности означает, что

Здесь и – постоянные

и функции, на которых определен оператор .

Условие линейности операторов можно записать так:

Операторы могут иметь векторный характер. В квантовой механике часто встречается оператор набла:

- орт-векторы (единичные).

Произведение 2-х векторных операторов строится как скалярное произведение векторов:

=

Оператор , для которого выполняется следующее равенство, наз. самосопряженным или эрмитовым:

От функций и требуется, чтобы оператор был определен на них и интегралы, входящие в это выражение, существовали.

Знак * означает комплексное сопряжение. Например, для выражения

Для получения комплексной сопряженности числа, содержащего мнимую единицу, нужно заменить на - : .Вещественный оператор при комплексном сопряжении остается неизменным.

СОБСТВЕННЫЕ ФУНКЦИИ И СОБСТВЕННЫЕ ЗНАЧЕНИЯ ОПЕРАТОРОВ

Когда в результате действия оператора на функцию, она не меняется или изменяется лишь на некоторый множитель, например, , то говорят, что – это собственное значение оператора , а функция - собственная функция оператора .

Условие, при котором оператор оставляет функцию f неизменной, с точностью до постоянного множителя, можно записать в виде: (1).

Здесь – постоянная, зависящая от вида оператора и функции. Очевидно, что не всякая функция f будет удовлетворять условию (1) и не при всяких значениях . Значения , при которых уравнение (1) имеет отличные от нуля решения, называются собственными значениями оператора . Набор собственных значений называется спектром собственных значений оператора . Спектр может быть непрерывным и дискретным. Он является непрерывным, если уравнение (1) имеет решение при всех значениях в некотором промежутке. Спектр собственных значений может быть смешанным, т.е. состоять из непрерывных и дискретных значений. Каждому собственному значению оператора соответствует собственная функция . В этом случае, говорят, что собственная функция принадлежит собственному значению . Если каждому собственному значению оператора принадлежит несколько различных функций , то говорят, что этот спектр -кратно вырожден. Рассмотрим несколько важных свойств собственных значений и собственных функций.

Теорема 1: Если оператор самосопряженный, то его собственные значения вещественны.

Теорема 2: Собственные функции и самосопряженного оператора , принадлежащие разным собственным значениям и ,ортогональны между собой:

. (2)

В случае дискретного спектра интеграл имеет конечное значение.

Если вместо функции выберем функцию , то имеем . Замена функции на таким способом называется нормированием функции , а коэффициент - коэффициентом нормировки.

Функция называется нормированной. Собственные функции дискретного спектра всегда можно считать нормированными.

Условие ортогональности и нормировки вместе можно записать следующим образом:

(4)

- символ Кронекера.

Возможны случаи, когда разные собственные функции принадлежат одинаковым собственным значениям, т.е. имеет место вырождение. Вырожденные функции вообще говорят не ортогональны.

Теорема 3: Если несколько собственных функций принадлежат одинаковым собственным значениям, то любая линейная комбинация из этих функций является решением того же операторного уравнения и с тем же собственным значением.

Теорема 4: Если 2 оператора и имеют общую полную систему собственных функций, они коммутируют.

Теорема 5: Если 2 оператора и коммутируют, то они имеют общие собственные функции.

Теорема 6: Система собственных функций операторного уравнения полна. Это значит, что любую функцию , определенную в той же области переменных и подчиненную тем же граничным условиям, что и собственные функции дискретного спектра оператора , можно представить в виде ряда из этих собственных функций: