Генераторы случайных чисел
Тема 3.5. Статистическое моделирование случайных величин
· метод Монте-Карло;
· идея метода;
· получение случайных величин.
Метод Монте-Карло
Рассматривание задачи в условиях неопределённости.
Неопределённость была стохастической. Строим математическую модель. Эта математическая модель является аналитической. В рассматриваемых задачах требовалось, чтобы рассматриваемые процессы были марковскими. На практике это не всегда выполняется.
В случаях, когда аналитические модели не приемлемы, строят статистические модели. Рассматривают метод статистического моделирования.
Статистические модели можно назвать имитационными. Они моделируют случайный процесс при помощи ПК.
Метод Монте-Карло является методом статистического моделирования.
Метод Монте-Карло - это численный метод решения задач при помощи моделирования случайных величин.
Происхождение метода Монте-Карло
Датой рождения метода Монте-Карло принято считать 1948г. создателями метода считают математиков Дж. Неймана и С. Улама.
Теоретическая основа метода была известна давно. Однако до появления ЭВМ этот метод не мог найти широкого применения.
Само название метода происходит от названия города Монте-Карло в княжестве Монако, знаменитого своими игорными домами. Дело в том, что одним из простейших механических приборов для получения случайных величин является рулетка. Возникает вопрос: помогает ли метод Монте-Карло выигрывать в рулетку? Нет, не помогает. И даже не занимается этим.
Идея метода
Идея метода чрезвычайно проста и состоит в следующем.
Вместо того, чтобы описывать процесс с помощью аналитического аппарата, проводится розыгрыш случайного явления с помощью специально организованной процедуры, включающей в себя случайность и дающей случайный результат. Реализация случайного процесса каждый раз складывается по-разному, т.е. мы получаем различные исходы рассматриваемого процесса. Это множество реализаций можно использовать как некий искусственно полученный статистический материал, который может быть обработан обычными методами математической статистики. После такой обработки можно получить: вероятность события, математическое ожидание и т. д.
Методом Монте-Карло может быть решена любая вероятностная задача, но оправданным он является тогда, когда процедура разыграна проще, а не сложнее аналитического расчета.
Пример
По цели производится 3 независимых выстрела, из которых каждый попадает в цель с вероятностью 1/2. Требуется найти вероятность хотя бы одного попадания.
Р(k >= 1) = P(1)+P(2)+P(3) = 1-P(k < 1)
P(0) = 1/2*1/2*1/2 = 1/8
P(k >= 1) = 1-1/8 = 7/8
Эту задачу можно решить розыгрышем - статистическим моделированием. Вместо 3 выстрелов будем бросать 3 монеты, считая, что герб - попадание, решка - промах. Опыт считается удачным, если на одной из монет выпадет герб. Проведем множество опытов, подсчитаем общее количество удач и разделим на число - N (количество проведённых опытов). Таким образом, они получили частоту события, а она при большом числе опытов близка к вероятности.
Метод Монте-Карло применяется: при моделировании случайных процессов, где присутствует множество случайных факторов.
Получение случайных величин
Таблица случайных чисел.
Выбирается случайная величина, распределенная по следующему закону:

Монтируется диск (рулетка). Диск вращается и резко останавливается, и выбирается та цифра, на которую указывает неподвижная стрелка.
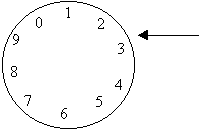
Ряд цифр 20389320...
Составляется таблица случайных чисел, выбирается определённое их количество (400).
Составит хорошую таблицу случайных чисел не так-то просто: любой реальный физический прибор вырабатывает случайные величины с распределением, несколько отличающимся от реального распределения.
Генераторы случайных чисел
Любой механический прибор будет слишком медленным для ЭВМ. Поэтому в качестве генераторов случайных чисел чаще всего используют шумы в электронных лампах (рис.8): если за некоторый промежуток времени уровень шума превысил заданный порог чётное число раз, то записывается единица *).
На первый взгляд это очень удобный способ. Пусть m таких генераторов работают параллельно, работают всё время и засылают случайные нули и единицы во все двоичные разряды специальной ячейки. Каждый такт - одно m-разрядное число. В любой момент счёта можно обратиться к этой ячейке и взять оттуда значение случайной величины, равномерно распределённой в интервале (0,1). Конечно, это значение приближенное, записанное в форме m-разрядной двоичное дроби
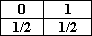
0,а1,а2,...аm, где каждая из величин ai имитирует случайную величину с распределением:
Однако и этот метод не свободен от недостатков. Во-первых, трудно проверить "качество" вырабатываемых чисел. Проверки приходится делать периодически, так как из-за каких-либо неисправностей может возникнуть так называемый дрейф распределения (т.е. нули и единицы в каком-либо из разрядов станут появляться не одинаково часто). Во-вторых, обычно все расчёты на ЭВМ проводят дважды, чтобы исключить возможность случайного сбоя. Но воспроизвести те же случайные числа невозможно, если их по ходу счёта не запоминать. А если их запоминать, то мы снова приходим к случаю таблиц.
Датчики такого типа, несомненно, окажутся полезными тогда, когда будут производиться специализированные ЭВМ для решения задач методом Монте-Карло. А для универсальных ЭВМ, на которых расчёты с помощью случайных чисел проводятся лишь изредка, содержать и эксплуатировать специальное устройство просто неэкономично. Лучше использовать так называемые псевдослучайные числа.
Псевдослучайные числа
Поскольку "качество" используемых случайных чисел проверяется с помощью специальных тестов, можно не интересоваться тем, как эти числа получены, лишь бы они удовлетворяли принятой системе тестов. Можно даже попытаться вычислять их по заданной формуле. Но, конечно, это должна быть весьма хитрая формула.
Числа, получаемые по какой-либо формуле и имитирующие значения случайной величины, называются псевдослучайными числами. Под словом "имитирующие" подразумевается, что эти числа удовлетворяют ряду тестов так, как если бы они были значениями этой случайной величины.
Первый алгоритм для получения псевдослучайных чисел был предложен Дж. Нейманом. Он называется методом середины квадратов. Поясним его на примере.
Пример
Пусть задано 4-значное число у0=0,9876. Возведём его в квадрат. Получим 8-значное число 0,97535376. Выберем четыре средние цифры этого числа и положим у1=0,5353. Затем возведём у1 в квадрат (0,28654609) и снова извлечём четыре средние цифры. Получим у2=0,6546. Далее, у2 в квадрате - 0,42850116, у3 = 0,8501; у3 в квадрате - 0,72267001, у4 = 0,2670; у4 в квадрате - 0,07128900, у5 = 0,1289 и т. д.
Но этот алгоритм не оправдал себя: получалось больше чем нужно малых значений. Поэтому разработаны другие алгоритмы.
Достоинства метода псевдослучайных чисел довольно очевидны. Во-первых, на получение каждого числа затрачивается несколько простых операций. Во-вторых, программа занимает всего несколько ячеек накопителя. В-третьих, любое из чисел может быть легко воспроизведено. И т.д.
Единственный недостаток - ограниченность количества псевдослучайных чисел.
Подавляющее большинство расчетов по методу Монте-Карло осуществляется c использованием псевдослучайных чисел.
Большинство алгоритмов для получения псевдослучайных чисел имеют вид

Если случайное число задано, то все последующие числа вычисляются по одной и той же формуле при k=1,2,3,...
Метод сравнений (метод вычетов)
Наиболее распространенный алгоритм для получения псевдослучайных чисел был предложен Д. Лемером. В основе этого алгоритма лежит функция у = {gx}, однако для удобства реализации на ЭВМ алгоритм строится несколько иначе.
Определяется последовательность целых чисел mk, в которой начальное число m0=1 задано, а все последующие числа m1,m2,.. вычисляются по одной и той же формуле
 (1)
(1)
при k=0,1,2,.. По числам mk вычисляются псевдослучайные числа

Формула (1) означает, что число mk+1 равно остатку, полученному при делении.
Отсюда происходят оба названия метода.