Лабораторна робота №3 Тема: Розв’язування задач лінійного програмування симплексним методом
Завдання:
1. Розв’язати задачу лінійного програмування симплексним методом.
2. Знайти відповідність симплексного розв’язку задачі лінійного програмування матричним перетворенням цієї задачі.
3. Розв’язати задачу лінійного програмування методом штучного базису.
1. Теоретичні відомості:
1) Розв’язування задач лінійного програмування симплексним методом підпорядковано наступному алгоритму:
· зведення умови задачі до канонічного виду, тобто, перетворення обмежень з системи нерівностей на систему еквівалентних рівнянь введенням додаткових невідомих;
· визначення початкового опорного плану задачі при врахуванні додаткових невідомих, як базисних;
· розрахунок рядка оцінок, як Δj=Zj-cj, де Zj – сума добутків коефіцієнтів стовпця Аj (стовпчик коефіцієнтів змінної хj) та відповідних коефіцієнтів стовпця Сбаз (стовпчик коефіцієнтів цільової функції базисних змінних), cj – коефіцієнт цільової функції змінної хj;
· розрахунок початкового значення цільової функції, як сума добутків коефіцієнтів стовпця А0 (стовпчик вільних членів канонічної системи лінійних рівнянь) та відповідних коефіцієнтів стовпця Сбаз;
· запис першої симплексної таблиці;
· перевірка оптимальності опорного плану за критерієм Δj=Zj-cj≥0 при умові знаходження максимуму цільової функції, або Δj=Zj-cj≤0, при умові її мінімізації;
· визначення стовпчиків, в яких слід вибирати розрахунковий елемент за критеріями: Δj=Zj-cj<0при умові знаходження максимуму цільової функції,Δj=Zj-cj>0 при умові знаходження мінімуму;
· визначення розрахункового елементу в одному з вибраних стовпчиків здійснюють за умови:
 ;
;
· вибір стовпчика з розрахунковим елементом здійснюють за умови порівняння відповідних добутків знайденого відношення θij на оцінку (Zj–cj): dj=[θij∙(Zj–cj)] для різних небазисних векторів. Максимальний серед них задовольнить умову максимальної зміни цільової функції та вкаже на вектор Aj, підходящий для введення в базис
· для переходу до наступного плану задачі виконують жорданові перетворення елементів таблиці за формулами:
ail*=ail/aij – для елементів рядка із розрахунковим коефіцієнтом,
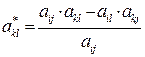 або
або 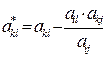 – для всіх інших елементів таблиці;
– для всіх інших елементів таблиці;
· новий план задачі перевіряють на оптимальність та при необхідності повторюють процедуру обчислень наступної таблиці.
2) Як можна було переконатися за результатами досліджень у попередній лабораторній роботі (ЛБ №2) жорданові перетворення еквівалентні матричним перетворенням системи лінійних рівнянь. Розв’язок задачі лінійного програмування, тобто оптимальні значення невідомих, також можна отримати за допомогою матричних перетворень, якщо знати матрицю-оператор D-1.
Розв’язок задачі заключає у собі результуюча матриця А*, яка є добутком матриці-оператора D-1 на розширену матрицю А коефіцієнтів невідомих та вільних членів системи рівнянь: А*=(D-1×А). Результуюча матриця А* відповідає числам записаним у останній симплексній таблиці.
Значення цільової функції можна знайти, як добуток C матриці-рядка коефіцієнтів базисних невідомих цільової функції на X0 матрицю-стовпчик значень цих невідомих: Z=C×X0. Значення Z записане у нижній клітині стовпчика А0 останньої симплексної таблиці. Числа стовпчика А0 у цій останній таблиці є оптимальними значеннями невідомих, а тому він позначений через X0.
Останній рядок кожної таблиці, позначений як (Zj-cj), який починається із стовпчика А1, відображає вираз цільової функції записаний через небазисні змінні, отже там записані коефіцієнти небазисних змінних. Щоб отримати ці коефіцієнти потрібно матрицю C помножити на відповідний стовпчик Аj і відняти коефіцієнт відповідної змінної початкового виразу цільової функції сj:
Zj-cj=C×Аj- сj.
2. Завдання:
Записати умову задачі Вашого варіанту із лабораторної роботи (ЛБ №1) та виконати записані далі завдання. Підсумком виконаної роботи має бути звіт про виконання завдань.
1). Розв’язати задачу симплексним методом.Для цього:
· Із системи обмежень Вашої задачі вилучити умову виробництва мінімальної сумарної кількості продукції. Задача набере вигляду де усі обмеження будуть мати знак «<»
· Задачу звести до канонічного виду.
· Відкрити вікно програми Microsoft Excel та записати першу симплексну таблицю. Задачі такого типу після введення додаткових змінних мають систему лінійних рівнянь з базисом, який утворюють ці додаткові змінні. А отже, задача пристосована до розв’язання її симплексним методом.
· Розв’язати задачу симплексним методом відповідно до наведеного вище алгоритму та записати її відповідь. Симплексний метод використовує жорданові перетворення, процедура застосування яких розглянута у ЛБ №2.
· Чи співпадає розв’язок знайдений симплексним методом із графічним розв’язком цієї задачі у ЛБ №1?
2). Провести аналіз розв’язку задачі з позицій матричної будови задачі та існуючих матричних співвідношень між структурними частинами симплексної таблиці. Для цього:
· Записати матрицю D, обернена до якої є оператором матричного розв’язку задачі.
· Скориставшись математичним забезпеченням програми Microsoft Excelзнайти обернену матрицю D-1.
· Порівняти обернену матрицю D-1 із стовпцями останньої симплексної таблиці, та знайти у цій таблиці таку саму матрицю.
· У якому місці останньої таблиці знаходиться матриця-оператор D-1? Яка причина її появи?
· Записати матрицю-рядок С (стовпчик коефіцієнтів цільової функції базисних змінних останньої таблиці), матрицю-стовпчик Х0 (числові значення базисних змінних останньої таблиці), розширену матрицю системи лінійних рівнянь А.
· Знайти результуючу матрицю А*=(D-1×А) та зробити висновок за отриманим результатом.
· Знайти значення цільової функції Z=(C×X0) та зробити висновок за отриманим результатом.
· Знайти оцінки стовпчиків результуючої матриці Zj-cj=C×Аj*- сj та зробити висновок за отриманим результатом.
· Три останні пункти завдань можна виконувати також для перевірки результатів у таблицях проміжних обчислень симплексного методу.
3). Виконати процедуру знаходження розв’язку повного варіанту задачі із ЛБ №1. У цьому випадку для знаходження початкового опорного плану задачі потрібно застосувати метод штучного базису. Метод описаний у лекційній частині курсу.
Цей варіант задачі передбачає введення у нерівності із знаком «>» окрім додаткового невідомого ще й штучного невідомого. Для обох цих невідомих має виконуватися умова невід’ємності значень. Крім того, на відміну від додаткових, штучні невідомі вводять у цільову функцію із коефіцієнтом «–М» для задач на пошук максимуму цільової функції, або із коефіцієнтом «+М» для задач на пошук мінімуму цільової функції. При обчисленні у вікні Microsoft Excelнеобмежено великому числу «М» достатньо приписати значення 1000 або навіть 100. Потрібно лише виконати умову, щоб число «М» було більше будь якого числа задачі, що з’являється у процесі її розв’язку.
3. Приклад:Маємо задачу лінійного програмування та її спрощений варіант:

| 
|
Зводимо спрощений варіант задачі до канонічного виду додаючи до лівої частини кожної нерівності додаткове невід’ємне невідоме.

Відкриваємо вікно програми Microsoft Excel тазаповнюємо першу симплексну таблицю. Далі за допомогою жорданових перетворень проводимо розрахунки, а потім у останній таблиці перетворень знаходимо відповідь задачі:
Вікно програми Microsoft Excel з розрахунками.

Максимум цільової функції Z=2214.286, X0=(32.86; 25.71; 0; 0; 16.43).
Скориставшись даними першої симплексної таблиці можна записати матричні співвідношення, які дозволяють знайти той самий розв’язок. Так матрицю D знайдемо у першій таблиці за ознаками, які знаходимо у останній симплексній таблиці, де бачимо, що базисний розв’язок складають невідомі у такій послідовності: х2(стовпчик А2), х1(стовпчик А1) та х5(стовпчик А5). Тому стовпцями матриці D є стовпчик А2, стовпчик А1 тастовпчик А5, що належать першій таблиці.
Скориставшись функцією «МОБР», перетворимо масив значень матриці D через команду Ctrl+Shift+Enter отримаємо числові значення елементів оберненої матриці D-1 (матрицю D-1 можна знайти у останній симплексній таблиці). Матриця D-1, як ми могли переконатися раніше, є оператором переходу від початкової системи лінійних рівнянь – матриці А до розв’язку задачі – матриці А*: А*=D-1×А.
Першим стовпчиком цієї матриці є оптимальні значення невідомих задачі X0=D-1×А0.
Значення цільової функції Z є сумою добутків цільових коефіцієнтів на числові значення базисних змінних розв’язку, а отже вона може бути записана у матричній формі як добуток матриці-рядка С та матриці-стовпця Х0. цільових коефіцієнтів: Z= С×А0.
У нижній частині сторінки бачимо результат знаходження виразу цільової функції через небазисні змінні (Zj-cj=C×Аj*- сj) у вигляді матриці-рядка. Цей результат співпадає із останнім рядком останньої симплексної таблиці.

Розглянемо розв’язок задачі лінійного програмування методом штучного базису. Для цього запишемо первинну умову задачі та зведемо її до канонічного виду:

Наявність від’ємного знаку біля додаткового невідомого х4 не дозволяє використати його для побудови початкового опорного розв’язку у симплексному методі. Тому продовжуємо вдосконалення математичної моделі задачі для створення можливості використання симплексного методу. У обмеження із «-х4» вводимо штучну змінну х7. Її також вводимо у цільову функцію приписавши коефіцієнт «-1000»

Задача у такому вигляді може бути розв’язана засобами програми Microsoft Excel, при цьому алгоритм розв’язку залишається той самий, що і для попереднього спрощеного варіанту задачі. На відміну від попереднього варіанту необхідно звернути увагу на заповнення рядка Zj-cj першої таблиці, Числа цього рядка обчислюють за допомогою функції «=СУММПРОИЗВ(C4:C7;D4:D7)» – у стовпцю А0 та формули «=СУММПРОИЗВ($C$4:$C$7;E4:E7)-E2» – у стовпцю А1, яку копіюють на інші клітинки рядка. Подальші обчислення значень змінних задачі аналогічні попередньому випадку.