Обнаружение ошибок в кодах Хемминга

Ошибка на выходе из канала связи может быть обнаружена и исправлена так (для построенного кода – не больше одной в каждом элементарном коде). Номер позиции S (записанный в двоичной системе), в которой произошла ошибка, определяется так:

S = S_k… S₂ S₁,

где S_i определяется по формулам (4) для элементарного кода, полученного на выходе канала связи. Если ошибки нет, то S_i = 0 и общий результат S = 0.

Пример 1: Пусть на вход канала связи поступил элементарный код 0110011 (т.е закодировано **1*011 (поз. 3,5,6,7– информационные, а контрольные члены заменены * )). На выходе получено 0110001 (искажен 6–й член элементарного кода). Вычислим S.

S₁= b₁+ b₃+ b₅+ b₇ = 0 + 1 + 0 + 1 = 0 (mod 2),

S₂= b₂ + b₃+ b₆+ b₇ = 1 + 1 + 0 + 1 = 1 (mod 2),

S₃= b₄+ b₅+ b₆+ b₇ = 0 + 0 + 0 + 1 = 1 (mod 2).

S= 1 1 0 = 6 (в десятичной системе).

Пример 2:Пусть на выходе получено 0111011 (искажен 4–й (контрольный) член элементарного кода).

S₁= b₁+ b₃+ b₅+ b₇ = 0 + 1 + 0 + 1 = 0 (mod 2),

S₂= b₂ + b₃+ b₆+ b₇ = 1 + 1 + 1 + 1 = 0 (mod 2),

S₃= b₄+ b₅+ b₆+ b₇ = 1 + 0 + 1 + 1 = 1 (mod 2).

S= S₃ S₂ S₁=1 0 0 = 4 (в десятичной системе).

Тогда восстановленное сообщение имеет вид: 0110011, а исходное сообщение – 1011(удалены контрольные члены, выделенные цветом)

Декодирование

После получения закодированного сообщения происходит его разбивка на элементарные коды, вычисление для каждого кода Sи в случае его неравенства 0 – корректировка соответствующего информационного члена (если S указывает на контрольный член, то корректировка не нужна). После удаления всех контрольных членов получаем исходное сообщение.

Примечание: Рассмотрено построение кодов Хемминга для бинарного кодирования и допустимом числе ошибок в элементарных кодах не более одной. Существует теория для построения таких кодов для равномерного кодирования любой арности и числе ошибок не более 2, 3,… и. д.

Алфавитное кодирование с минимальной избыточностью

Пусть задано алфавитное кодирование со схемой å

a₁® B₁

a₂® B₂

a₃® B₃

….

a_r® B_r

Слова B_i заданы в алфавите O ={b₁,b₂,b₃….b_q } , где q – число букв алфавита O l_i = l (B_i) ( i= 1,…,r ) ( длины элементарных кодов).

Теорема 1 Если алфавитное кодирование со схемой å обладает свойством взаимной однозначности, то выполняется следующее неравенство (неравенство Макмиллана):

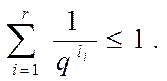
(5)

Теорема 2 Если l_i целые числа, удовлетворяющие неравенство (5) , то существует алфавитное кодирование со схемой å¢, обладающей свойством префикса и для которого l (B₁) = l₁, …, l (B_r) = l_r .

Пояснения.

1. Неравенство Макмиллана является необходимым и достаточным условием существования алфавитного кодирования, у которого схема обладает свойством префикса и длины элементарных кодов равны соответственно l₁, l₂,…, l_r .

2. Нельзя построить схему алфавитного кодирования, обладающую свойством взаимной однозначности, если неравенство (3.5) нарушено.

3 Теоремы 1 и 3 не дают полного алгоритма построения схемы алфавитного кодирования, обладающей свойством взаимной однозначности (если выполняется неравенство 5 – такая схема существует и можно продолжать ее построение, используя другие свойства и теоремы).

Рассмотрим кодирование информации в компьютере. Исторически сложилось, что компьютерный алфавит элементарных кодов O ={ b₁,b₂…} состоит только из двух символов {0, 1} т.е. q = 2. При алфавитном кодировании (кодировании символов) используются элементарные коды одинаковой длины равной 8. В этом случае автоматически решается вопрос взаимной однозначности схемы кодирования (алгоритм декодирования следующий – закодированное сообщение разбивается с конца или начала на фрагменты по 8 символов, каждому из фрагментов соответствует символ входного алфавита). Максимальное значение r , для которого выполняется неравенство (5) определяется из уравнения r = q ⁸;2⁸=256 . Другими словами, при такой схеме кодирования можно закодировать алфавит I максимум из 256 символов. В данном случае код сообщения будет в 8 раз длиннее самого сообщения. В общем виде превышение длины кода сообщения над длиной самого сообщения определится из формулы (длина элементарных кодов одинакова):

l = ]log_q r [ (наименьшее целое число не меньшее логарифма r по основанию q). Если схема кодирования такова, что элементарные коды имеют различную длину, то можно говорить о величине среднего превышения длины кода над длиной самого сообщения:

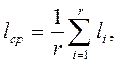где l_i = l (B_i) (6)

Если имеется статистика о вероятности появления символов входного алфавита

I={ a₁,a₂,…, a_r } в сообщениях, p₁, p₂, …p_r соответственно, то формула (6) примет вид:

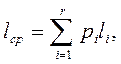(7)

Эта характеристика может изменяться как при переходе от одной схемы кодирования к другой, так и при изменении вероятностных характеристик источника сообщений. Введем для фиксированного источника сообщений характеристику l^*.

l^* = (8)

В формуле (8) минимум берется по всем схемам кодирования å, обеспечивающим свойство взаимной однозначности.

Оценим интервал значений l_ср для схем кодирования å, обеспечивающих свойство взаимной однозначности.

1 ≤ l_ср ≤ ]log_q r[ (9)

Верхнюю оценку дает кодирование с элементарными кодами одинаковой длины, нижнюю – простая замена одних символов другими (можно наблюдать при просмотре Web –страниц с неправильной кодировкой). Значит при поиске оптимальной (в смысле минимизации l_ср) схемы кодирования, схемы, у которых l_ср > ]log_q r [ можно сразу исключить из рассмотрения. В соответствии с формулой (7) для предварительного определения длины элементарных кодов p_i l_i ≤ ]log_q r[ . Поскольку при вычислении члены суммы с p_i = 0 не играют роли, то, положив p_* = min (p_i), имеем :

(10)

Определение. Коды, определяемые схемой å с l_ср= l^*, называют кодами с минимальной избыточностью, или кодами Хаффмана.

Такие коды дают в среднем минимальное увеличение длин слов при кодировании сообщений заданного источника. Представляет практический интерес задача построения таких кодов (схем кодирования) для источника сообщений с фиксированными характеристиками (в силу вышеизложенного можно ограничиться рассмотрением только схем кодирования, обладающих свойством префикса).

Построение кодов Хаффмана

Обобщим представление об алфавитном кодировании. Каждой схеме алфавитного кодирования å со свойством префикса можно поставить в соответствие кодовое дерево (связный ациклический неориентированный граф), которое является частью обобщенного кодового дерева. Обобщенное кодовое дерево строится так:

Ø выбирается начальная вершина (нулевой ярус дерева m = 0 );

Ø из этой вершины выходит пучок ребер, количество которых равно q (мощность алфавита O ), и каждому из них приписано значение элементов алфавита O={b₁,b₂…} (первый ярус дерева m = 1 );

Ø из каждой вершины первого яруса снова выходит пучок ребер, количество которых равно q, и которые обозначены элементами алфавита O (второй ярус дерева m = 2 );

Ø аналогично строятся третий, четвертый и т.д. ярусы;

Кодовое дерево для конкретной схемы кодирования со свойством префикса будет являться частью обобщенного дерева, причем каждому элементарному коду должна соответствовать концевая вершина этого дерева, а начальные вершины должны совпадать.

На рисунке 1 показано обобщенное кодовое дерево для q = 3. Количество вершин на каждом ярусе равно q ^m(на первом – 3, на втором – 9, на третьем – 27 и т.д.). При равномерном алфавитном кодировании все элементарные коды имеют одинаковую длину.

С использованием вершин первого яруса как концевых, можно закодировать максимум 3х –символьный входной алфавит, второго 9ти – символьный и т.д. Если r в точности равно q ^m, то кодом Хаффмана будет схема кодирование элементарными кодами длины m из m–го яруса кодового дерева. Элементарные коды B_i записываются как цепи, соединяющие начальную вершину кодового дерева с каждой из вершин m–го яруса.

Более сложный случай, когда

q ^m< r < q ^m⁺¹,(11)

(для конкретного значения r всегда можно подобрать целое m, удовлетворяющее этому неравенству).

Общие принципы поиска кода (схемы кодирования) с минимальной избыточностью:

§ для построения элементарных кодов использовать только m и m+1 ярусы кодового дерева;

§ переходить на m+1 ярус можно только после исчерпания всех возможностей m– го яруса.

Для реализации этого алгоритма необходимо представить r в виде:

r = (q ^m–n)+ q ×n – t, (12)

где n - число вершин в кодовом дереве яруса m, которые ветвятся в m+1 ярус;

t число вершин m+1 яруса, не задействованных при построении схемы кодирования ( t < q).

Формула для определения l^*будет иметь следующий вид:

l^* = [( q ^m– n) × m + (q ×n – t)( m+1)]/ r (13)

Если имеется информация о вероятности появления символов входного алфавита

I={ a₁,a₂,…, a_r } в сообщениях, p₁, p₂, …p_r соответственно, то задача построения кода Хаффмана существенно усложняется. Взаимная однозначность кодирования обеспечивается использованием при составлении элементарных кодов обобщенного кодового дерева, при этом концевым вершинам дерева, соответствующего схеме кодирования, приписываются вероятности p₁, p₂, …p_r , а внутренним вершинам i–го яруса суммы вероятностей тех вершин i+1 –го яруса, которые исходят из них. Для изложения алгоритма построения кодов Хаффмана приведем ряд теоретических положений.

Лемма 1 Для кода с минимальной избыточностью из условия p_j < p_i следует, что

l _j ³ l_j .

Следствие. В кодовом дереве для кода с минимальной избыточностью вероятности, приписанные концевым вершинам из m–го яруса не меньше, чем вероятности, приписанные концевым вершинам из m +1–го яруса.

Определение. Неконцевая вершина кодового дерева называется насыщенной, если ее порядок ветвления равен q . Кодовое дерево называется насыщенным, если в нем насыщены все неконцевые вершины, за исключением, быть может, одной, лежащей в предпоследнем ярусе, и порядок ветвления этой вершины равен q_о,где 2 ≤ q_о< q (если в насыщенном дереве нет исключительной вершины, то будем считать, что q_о= q и роль исключительной может играть любая вершина из предпоследнего яруса). При решении задач для определения порядка ветвления исключительной вершины находят остаток от деления r / (q –1) и назначают q_о в соответствии с (14):

(14)

Лемма 2 Среди кодов с минимальной избыточностью существует код, кодовое дерево которого является насыщенным.

Теорема 3 Среди кодов с минимальной избыточностью существует приведенный код (схема кодирования), причем q_о определяется в соответствии с (14).

Приведенным будем называть такое кодовое дерево, в котором концевым вершинам, выходящим из q_о приписаны минимальные вероятности.

Описание алгоритма поиска кода с минимальной избыточностью (кода Хаффмана) для случая алфавитного кодирования, если имеется информация о вероятности появления символов входного алфавита.

1 Определить q_о по формуле (14).

2 Упорядоченный по убыванию список вероятностей p₁, p₂, …p_r заменяют новым упорядоченным списком вида: p₁, p₂,.. p_j_, p,…p_r_–_qo, где p = p_r_–_qo₊₁+ …+ p_r (т.е. суммируют последние q_о элементов списка и создают новый упорядоченный список, в который входит как элемент полученная сумма); процесс суммирования и упорядочивания (но уже суммируют последние q элементов) продолжается до тех пор, пока в списке вероятностей останется ровно q элементов.

3 Для последнего свернутого по п.2 списка строится одноярусное кодовое дерево (из начальной вершины выходит q ребер, каждому из которых приписывается буква алфавита O, а каждой вершине 1–го яруса вероятности из последнего свернутого списка).

4 Построить 2–й, 3–й и другие ярусы кодового дерева, на которых развернуть просуммированные вероятности последнего, предпоследнего и т.д. списков(вершины, которым приписаны вероятности букв входного алфавита на любом ярусе, становятся концевыми); в результате таких действий получим кодовое дерево, в котором r концевых вершин и каждой из которых приписана вероятность p_j .Выписав цепи из нулевой вершины к концевым (перечень ребер), получим схему кодирования с минимальной избыточностью.

Пример1: Построить код с минимальной избыточностью (код Хаффмана) для следующих исходных данных:

r	q	p₁, p₂, …p₁₂
		0,26; 0,22; 0,14…

Решение

1 Определить q_о по формуле (14).

k = ]r/ (q –1)[ (остаток от деления)

k =] 7/2[ = 1; q₀ = 3.

2 Упорядоченный список вероятностей 1 (7 чисел):

0,26; 0,22; 0,14; 0,10; 0,10; 0,09; 0,09 (курсивом выделены числа, которые суммируются при формировании списка 2).

Упорядоченный список 2 (5 чисел) 0,28; 0,26; 0,22; 0,14; 0,10

Упорядоченный список 3 (3 числа) 0,46; 0,28; 0,26;

3 Для последнего свернутого в п.2 списка строится одноярусное кодовое дерево (из начальной вершины выходит 3 ребра, каждому из которых приписывается буква алфавита O, а каждой вершине 1–го яруса вероятности из последнего свернутого списка).

4 Строим 2–й, 3–й и другие ярусы кодового дерева, на которых разворачиваем просуммированные вероятности последнего, предпоследнего и т.д. списков(вершины, которым приписаны вероятности букв входного алфавита на любом ярусе, становятся концевыми); в результате таких действий получим кодовое дерево, в котором r концевых вершин и каждой из которых приписана вероятность p_j .Выписав цепи из нулевой вершины к концевым (перечень ребер), получим схему кодирования с минимальной избыточностью.

Величина среднего превышения длины закодированного сообщения над длиной самого сообщения определим по формуле:

l^* = = 0,26 + (0,28+0,46)х2 = 1,74.

Пример2: Построить код с минимальной избыточностью (код Хаффмана) для следующих исходных данных:

r	q

Решение

q =3; r = 7 в соответствии с формулой (12) m = 1. Для кодирования будет достаточно 1–го и 2–го ярусов обобщенного кодового дерева (см. рис. 3).

r =(q ^m –n)+ q ×n – t, 7 = (3 –n)+ 3 n – t (подбираем целые n и t)

Равенство выполняется для n = 2 и t= 0.

Определим l^* для полученной схемы по формуле (13)

l^*= [( q ^m– n) × m + (q ×n – t)( m+1)]/ r

l^* = (( 3-2) х1 + (3х2 – 0) (1+1)) / 7 = 13/7 = 1,86.