Краткие теоретические сведения. 1. Повторить теоретический материал по теме 4.2.1.3 «Итерационный матричный алгоритм разрезания графа» по конспекту и по [1]

Программа работы

 

1. Повторить теоретический материал по теме 4.2.1.3 «Итерационный матричный алгоритм разрезания графа» по конспекту и по [1].

2. Разрезать граф принципиальной электрической схемы, полученный для своего варианта изделия в практической работе № 2, на три куска. Количество вершин n_i в кусках в зависимости от количества вершин в графе указано в таблице 1.

 

Таблица 1

Количество вершин в графе	Количество вершин в кусках	Количество вершин в графе	Количество вершин в кусках
G1	G2	G3	G1	G2	G3

 

3. Определить коэффициент разрезания графа.

4. Сделать вывод по работе, указав достоинства и недостатки итерационного матричного метода разрезания графа.

5. Дать предложения по совершенствованию данного метода.

6. Составить отчёт о выполнении работы.

Отчёт по практической работе оформляется на листах формата А4 в соответствии с ГОСТ 2.105-79.

Отчет по практической работе должен содержать:

1) номер работы;

2) название работы;

3) цель работы;

4) задание с указанием номера заданного варианта;

5) описание процесса разрезания графа на куски итерационным матричным методом применительно к своему варианту задания;

6) результат разрезания графа заданного варианта принципиальной электрической схемы;

7) результат разбиения принципиальной электрической схемы изделия РЭС на отдельные конструктивно законченные части (блоки);

8) сравнить количество внешних связей между сформированными кусками графа с количеством внешних связей между скомпонованными блоками (физическими) РЭС.

Краткие теоретические сведения

 

 

Любой граф можно описать матрицей смежности R, поэтому разрезание графа G на l кусков G₁, G₂,…, G_l эквивалентно разбиению матрицы на клетки. В случае матрицы смежности R разрезание графа соответствует разрезанию матрицы на l² клеток (подматриц) как показано на рис. 1.

 

		x1	x2	x3	…	xi	…	xj	…	xn
	x1	G1
	x2
	x3
R =	…				G2
	xi
	…
	xj							G3
	…
	xn

 

Рис. 1

Клетки (подматрицы), расположенные по главной диагонали матрицы R, соответствуют кускам G_i графа G. Элементы, расположенные в диагональных клетках, определяют количество рёбер, соединяющих вершины куска G_i между собой (внутренние связи). Элементы, расположенные в остальных клетках, определяют количество рёбер, соединяющих куски между собой (внешние связи).

Задача разрезания графа на куски применительно к матричному методу формулируется следующим образом.

Пусть задан граф G = (X, U), имеющий n вершин и r рёбер. Требуетсяразрезать граф на куски так, чтобы получить максимальное значение функции

 

L = 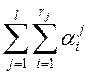(1)

 

где L – суммарное количество рёбер внутри всех кусков графа;

a^j_i = 1, если u_j Î U_ij,

a^j_i = 0 в противном случае,

U_шо – множество внутренних рёбер куска G_j;

|U_ij| = r_j

Задаётся стандартная матрица F = ||f_ij||_n, i, j Î J = {1, 2, …, n}, в которой по главной диагонали расположено столько единичных подматриц, на сколько кусков разрезается граф G. Порядок единичной подматрицы определяется количеством вершин, которое должно быть помещено в кусок G_i после разрезания графа.

Матрица смежности R разбивается на подматрицы в соответствии с разбиением матрицы F. Разбиение матрицы R в определённом смысле эквивалентно случайному разрезанию графа G на заданное количество кусков.

Методику разрезания графа G на куски матричным методом рассмотрим на примере выполнения конкретного задания. На рис. 2 представлен граф G принципиальной электрической схемы автоматического зарядного устройства. Разрезание этого графа на три куска по четыре вершины в каждом последовательным и итерационным методом с использованием чисел связности было рассмотрено в методических разработках к практическим работам №№ 3 и 4.

 

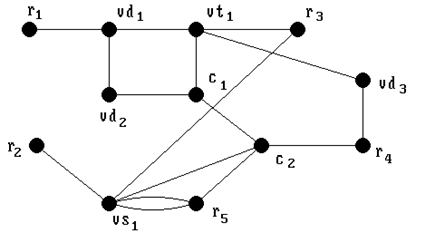
Рис. 2

 

Задание

 

1)Разрезать граф G (рис. 2) на трикуска почетыре вершины в каждом.

2)Определить коэффициент разрезания.

3)Сравнить полученный результат с результатами выполнения практических работ №№ 3, 4.

Решение

 

1) Построить стандартную матрицу F, выделив в ней единичные подматрицы, соответствующие заданному разрезанию графа.

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

r2

r3

r4

r5

F =

c1

(2)

c2

vd1

vd2

vd3

vt1

vs1

2) Построить матрицу смежности R и разбить её на подматрицы в соответствии с разбиением матрицы F.

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

r2

r3

r4

r5

R =

c1

(3)

c2

vd1

vd2

vd3

vt1

vs1

 

Указанному разрезанию матрицы смежности R соответствует разрезание графа G, показанное на рис. 3. Общее количество рёбер внутри кусков L = 3, а количество внешних связей между кусками K = 13. Коэффициент разрезания графа D(G) = 3/13 = 0,23.

Рис. 3. Разрезание графа, соответствующее разрезанию матрицы смежности (3)

 

Для максимизации функции L необходимо выполнить перестановки строк и столбцов матрицы смежности (3). С этой целью вводятся некоторые вспомогательные матрицы

3) Построить вспомогательную матрицу M = ||m_ij||_n, где i, j Î J = {1, 2, …, n}, как результат умножения матриц Fи R:

 

M = F Ä R(4)

 

Элементы матрицы M вычисляются по формулам:

 

m_ij = , m_ji = (5)

 

Для рассматриваемого графа G матрица M будет иметь вид:

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

r2

r3

r4

r5

M =

c1

(6)

c2

vd1

vd2

vd3

vt1

vs1

 

Ниже приведены примеры использования формул (5) для вычисления некоторых значений элементов матрицы M.

m₁₁ = f₁₁ × (r₁, r₁) + f₁₂ × (r₁, r₂) + f₁₃ × (r₁, r₃) + f₁₄ × (r₁, r₄) + f₁₅ × (r₁, r₅) +

+ f₁₆ × (r₁, c₁) + f₁₇ × (r₁, c₂) + f₁₈ × (r₁, vd₁) + f₁₉ × (r₁, vd₂) + f₁₁₀ × (r₁, vd₃) +

+ f₁₁₁ × (r₁, vt₁) + f₁₁₂ × (r₁, vs₁) =

= 1 × 0 + 1 × 0 + 1 × 0 + 1 × 0 + 0 × 0 + 0 × 0 + 0 × 1 + 0 × 1 + 0 × 0 + 0 × 1 + 0 × 2 = 0

m₁₇ = f₁₁ × (c₂, r₁) + f₁₂ × (c₂, r₂) + f₁₃ × (c₂, r₃) + f₁₄ × (c₂, r₄) + f₁₅ × (c₂, r₅) +

+ f₁₆ × (c₂, c₁) + f₁₇ × (c₂, c₂) + f₁₈ × (c₂, vd₁) + f₁₉ × (c₂, vd₂) + f₁₁₀ × (c₂, vd₃) +

+ f₁₁₁ × (c₂, vt₁) + f₁₁₂ × (c₂, vs₁) =

= 1 × 0 + 1 × 0 + 1 × 0 + 1 × 1 + 0 × 1 + 0 × 1 + 0 × 0 + 0 × 0 + 0 × 0 + 0 × 0 + 0 × 1 = 1

…

m₁₁₂ = f₁₁ × (vs₁, r₁) + f₁₂ × (vs₁, r₂) + f₁₃ × (vs₁, r₃) + f₁₄ × (vs₁, r₄) + f₁₅ × (vs₁, r₅) +

+ f₁₆ × (vs₁, c₁) + f₁₇ × (vs₁, c₂) + f₁₈ × (vs₁, vd₁) + f₁₉ × (vs₁, vd₂) + f₁₁₀ × (vs₁, vd₃) +

+ f₁₁₁ × (vs₁, vt₁) + f₁₁₂ × (vs₁, vs₁) =

= 1 × 0 + 1 × 1 + 1 × 1 + 1 × 0 + 0 × 2 + 0 × 0 + 0 × 1 + 0 × 0 + 0 × 0 + 0 × 0 + 0 × 0 = 2

…

m₈₁₂ = f₈₁ × (vs₁, r₁) + f₈₂ × (vs₁, r₂) + f₈₃ × (vs₁, r₃) + f₈₄ × (vs₁, r₄) + f₈₅ × (vs₁, r₅) +

+ f₈₆ × (vs₁, c₁) + f₈₇ × (vs₁, c₂) + f₈₈ × (vs₁, vd₁) + f₈₉ × (vs₁, vd₂) + f₈₁₀ × (vs₁, vd₃) +

+ f₈₁₁ × (vs₁, vt₁) + f₈₁₂ × (vs₁, vs₁) =

= 0 × 0 + 0 × 1 + 0 × 1 + 0 × 0 + 1 × 2 + 1 × 0 + 1 × 1 + 1 × 0 + 0 × 0 + 0 × 0 + 0 × 0 +

+ 0 × 0 = 2 +1 = 3

…

Процесс продолжается до тех пор, пока не будут найдены все элементы матрицы M. Матрица M не является симметричной, т.е. в общем случае m_ij¹ m_ji.

4)Построить вспомогательную матрицу B = ||b_ij||_n, где i, j Î J = {1, 2, …, n}. Матрица B представляет собой результат поэлементного перемножения матриц `F и R:

 

B = `F ´ R(7)

 

где `F – инверсия матрицы F, т.е. каждый единичный элемент матрицы F заменяется на нулевой и наоборот.

Для рассматриваемого примера матрица `F имеет вид:

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

r2

r3

r4

r5

``F =

c1

(8)

c2

vd1

vd2

vd3

vt1

vs1

 

Элемент b_ij матрицы B определяется по формуле:

 

b_ij = `f_ij × r_ij (9)

 

где `f<sub>ij</sub> – элемент матрицы `F.

Элементы первой строки матрицы B равны:

b₁₁ = `f<sub>11</sub> × (r<sub>1</sub>, r<sub>1</sub>) = 0; b<sub>12</sub> = `f₁₂ × (r₁, r₂) = 0; b₁₃ = `f₁₃ × (r₁, r₃) = 0;

b₁₄ = `f<sub>14</sub> × (r<sub>1</sub>, r<sub>4</sub>) = 0; b<sub>15</sub> = `f₁₅ × (r₁, r₅) = 0; b₁₆ = `f₁₆ × (r₁, c₁) = 0;

b₁₇ = `f<sub>11</sub> × (r<sub>1</sub>, c<sub>2</sub>) = 0; b<sub>18</sub> = `f₁₈ × (r₁, vd₁) = 1; b₁₉ = `f₁₉ × (r₁, vd₂) = 0;

b₁₁₀ = `f<sub>110</sub> × (r<sub>1</sub>, vd<sub>3</sub>) = 0; b<sub>111</sub> = `f₁₁₁ × (r₁, vt₁) = 0; b₁₁₂ = `f₁₁₂ × (r₁, vs₁) = 0;

Аналогично определяются все остальные элементы матрицы. В результате будет получена вспомогательная матрица B:

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

r2

r3

r4

r5

B =

c1

(10)

c2

vd1

vd2

vd3

vt1

vs1

 

Матрица B является симметричной относительно главной диагонали: b_ij=b_ji.

5) Построить вспомогательную матрицу P = ||p_ij||_n, где i, j Î J = {1, 2, …, n}. Матрица P определяется с помощью матриц M и B по формулам:

p_ij = m_ij – b_ij; p_ij = m_ij – b_ij(11)

 

Как следует из (11), матрица P не является симметричной.

Для рассматриваемого примера матрица P будет иметь вид:

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

r2

r3

r4

r5

P =

c1

(12)

c2

vd1

vd2

vd3

vt1

vs1

 

6) Для максимизации значения функции (1) после случайного разрезания графа необходимо выбрать пару вершин, принадлежащих разным кускам графа и переставить их, если значение L при этом увеличивается. Перестановочные коэффициенты определяются по формуле:

 

h_ij = p_ij + p_ji – (p_ii + p_jj) (13)

 

Следует заметить, что вершины x_i и x_j принадлежат разным кускам. Отсюда следует, что первые два члена выражения (13) характеризуют внешние связи между кусками, а вторые два (в скобках) – внутренние. В таком случае положительное максимальное значение h_ij является условием для перестановки вершин из одного куска в другой. Для определения перестановочных коэффициентов целесообразно построить матрицу H = ||h_ij||_n, где i, j Î J = {1, 2, …, n}. Так как матрица H строится только по результатам операций с элементами симметричной матрицы P, то матрица H также будет симметричной, поэтому достаточно построить только треугольную полуматрицу.

 

r1

r2

r3

r4

r5

c1

c2

vd1

vd2

vd3

vt1

vs1

r1

+2

r2

-1

-1

-1

+1

+1

+1

+1

+1

r3

-1

-1

-1

+1

+2

+2

+2

r4

-2

+2

+1

-1

+1

+3

r5

+1

+2

H =

c1

+1

+4

(14)

c2

+1

-2

vd1

+2

+1

+1

+5

vd2

vd3

vt1

vs1

 

 

Наибольшее положительное значение имеет элемент h_8-12, расположенный на пересечении строки vd₁ и столбца vs₁. После перемещения вершины vd₁ из куска G₂ в кусок G₃, а вершины vs₁ – из куска G₃ в кусок G₂ общее количество L рёбер внутри кусков увеличится на и 5 станет равным 8. Соответственно количество внешних связей K между кусками графа уменьшится и станет равным 8 (рис. 4). Коэффициент разрезания графа DG = 8/8 = 1.

 

 

Рис. 4. Разрезание графа G после перестановки вершин vd₁ и vs₁

 

7) Переставить строки и столбцы vd₁ и vs₁ в матрице смежности (5.3). В результате будет получена матрица R⁽¹⁾:

 

 

r1

r2

r3

r4

r5

c1

c2

vs1

vd2

vd3

vt1

vd1

r1

r2

r3

r4

r5

R(1) =

c1

(15)

c2

vs1

vd2

vd3

vt1

vd1

8) По матрицам F (2) и R⁽¹⁾ (15) построить вспомогательную матрицу M⁽¹⁾. Матрица F будет оставаться неизменной до полного окончания процесса разрезания графа.

 

r1

r2

r3

r4

r5

c1

c2

vs1

vd2

vd3

vt1

vd1

r1

r2

r3

r4

r5

M(1) =

c1

(16)

c2

vs1

vd2

vd3

vt1

vd1

9) Построить вспомогательную матрицу B⁽¹⁾, используя матрицы `F и R<sup>(1)</sup>. Матрица `F является инверсией матрицы F, поэтому она также будет неизменной до окончания решения задачи.

 

r1

r2

r3

r4

r5

c1

c2

vs1

vd2

vd3

vt1

vd1

r1

r2

r3

r4

r5

B(1) =

c1

(17)

c2

vs1

vd2

vd3

vt1

vd1

 

10)По матрицам M⁽¹⁾ и B⁽¹⁾, руководствуясь формулой (11), построить вспомогательную матрицу P⁽¹⁾.