МЕХАНИЧЕСКИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
Физика
Механика
«Определение момента инерции физического маятника» 
Методические указания к лабораторной работе №7 для направления подготовки
| специалистов: | 130400.65 | - Горное дело |
| 190109.65 | - Наземные транспортно-технологические средства | |
| бакалавров: | 080200.62 | - Менеджмент |
| 140400.62 | - Электроэнергетика и электротехника | |
| 220400.62 | - Управление в технических системах | |
| 270800.62 | - Строительство | |
| 190600.62 | - Эксплуатация транспортно-технологических машин и комплексов |
Губкин 2011
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное учреждение
высшего профессионального образования
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ ОТКРЫТЫЙ УНИВЕРСИТЕТ
ИМ. В.С. ЧЕРНОМЫРДИНА
Губкинский институт (филиал)
УТВЕРЖДЕНО
Директором Губкинского
института (филиала) МГОУ

Физика
Механика
«Определение момента инерции физического маятника» 
Методические указания к лабораторной работе №7 для направления подготовки
| специалистов: | 130400.65 | - Горное дело |
| 190109.65 | - Наземные транспортно-технологические средства | |
| бакалавров: | 080200.62 | - Менеджмент |
| 140400.62 | - Электроэнергетика и электротехника | |
| 220400.62 | - Управление в технических системах | |
| 270800.62 | - Строительство | |
| 190600.62 | - Эксплуатация транспортно-технологических машин и комплексов |
Губкин, 2011
УДК 53
Ф 50
Физика. Часть 1. Определение момента инерции физического маятника: Методические указания к лабораторной работе№ 7 / Сост. А.Н.Ряполов; Рец. д.ф.-м.н., профессор, зав. кафедрой физики КГТУ В.М. Полунин, к.т.н., профессор кафедры "Теоретической и прикладной механики" ГИ(филиала) МГОУ А.И. Гарбовицкий.- Губкин.: МГОУ, 2011.- 12с.
Методические указания включают рекомендации и указания по выполнению лабораторной работы, в которой определяется момент инерции физического маятника. Указания содержат краткую теоретическую часть; описание экспериментальной установки, порядок выполнения работы, контрольные вопросы и указана литература по теории.
Предназначены для студентов технических специальностей вузов.
© Губкинский институт (филиал) Московского государственного открытого университета, 2011.
© А.Н. Ряполов, 2011.
ЛАБОРАТОРНАЯ РАБОТА № 7
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ФИЗИЧЕСКОГО МАЯТНИКА
Цель работы: экспериментальное определение момента инерции длинного стержня.
Приборы и принадлежности: длинный стержень, секундомер, линейка с миллиметровыми делениями, зажим с полкой.
ВВЕДЕНИЕ
В физике колебательным (или периодическим) называется процесс, который обладает той или иной степенью повторяемости во времени.
Одной из основных характеристик колебательного процесса является период колебаний. Периодом колебаний T называется время, за которое совершается одно полное колебание.
Величину обратную периоду колебаний, называют частотой колебаний и обозначают буквой n.
По определению
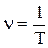 (1)
(1)
Из формулы (1) следует, что частота определяет число полных колебаний за единицу времени. Единицей измерения частоты является герц (Гц). Герц - частота колебаний, период которых равен одной секунде, т.е.
1 Гц = 
Среди множества существующих видов колебательных процессов простейшими являются гармонические колебания.
Гармоническим колебанием называется периодический процесс, при котором колеблющаяся величина изменяется со временем по закону синуса и косинуса. Например, в случае одномерного гармонического колебания значение колеблющейся величины во времени изменяется по закону синуса и косинуса. Например, в случае одномерного гармонического колебания значение колеблющейся величины во времени изменяются по закону
 (2)
(2)
График одномерного гармонического колебательного движения, описываемого функцией, представлен на рис. 1.
 |
Рассмотрим смысл величин, входящих в формулу (2):
х - величина отклонения значения колеблющейся величины в момент времени t от ее значения при равновесии системы/
A - амплитуда колебания представляет собой абсолютную величину максимального значения х.
Поскольку косинус имеет пределы изменения  , значение колеблющейся величины х в выражении (2) может соответственно меняться в пределах
, значение колеблющейся величины х в выражении (2) может соответственно меняться в пределах  .
.
Величина аргумента косинуса  называется фазой колебания и, являясь функцией времени, определяет значение величины х в данный момент времени t.
называется фазой колебания и, являясь функцией времени, определяет значение величины х в данный момент времени t.
Параметр a в формуле (2) называется начальной фазой колебания, которая характеризует значение колеблющейся величины хо в начальный момент времени, т.е.

где  - значение колеблющейся величины при t=0.
- значение колеблющейся величины при t=0.
Величина w называется циклической (круговой) частотой колебаний.
Поскольку одному колебанию при a=0 соответствует изменение аргумента косинуса на величину  , можно записать
, можно записать
 (3)
(3)
Таким образом, циклическая частота численно равна числу полных колебаний, совершаемых за время, равное  секунд.
секунд.

Циклическая частота  измеряется в радианах за секунду (рад/сек).
измеряется в радианах за секунду (рад/сек).
МЕХАНИЧЕСКИЕ ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
До сих пор мы рассматривали процесс колебаний в его общем виде. Перейдем к конкретному случаю.
Какова должна быть сила, действующая на материальную точку массой m, для того чтобы эта точка совершала гармонические колебания?
Поскольку гармоническое колебательное движение в нашем случае является одним из видов механического движения, для него справедлив основной закон динамики - второй закон Ньютона.
 (4)
(4)
где a - ускорение, которым обладает движущаяся материальная точка под действием результирующей всех сил, действующих на эту точку.
Найдем выражение скорости и ускорения при гармоническом колебательном движении.
Для этого вспомним, что мгновенное значение скорости представляет собой первую производную от пути (смещения) по времени
 (5)
(5)
а мгновенное значение ускорения - первую производную от скорости по времени:
 (6)
(6)
Продифференцировав выражение (2), получим скорость
 (7)
(7)
Амплитуда скорости при гармоническом колебании равна произведению амплитуды А смещения на циклическую частоту 
Продифференцировав выражение (7), получим
 (8)
(8)
Перепишем выражение для ускорения при гармоническом колебательном движении (с учетом (2)):
 (9)
(9)
Тогда на равенства (4) и (9) получим выражение, определяющее величину силы, вызывающей гармонические колебания:
 (10)
(10)
Из формулы (10) видно, что для того, чтобы материальная точка совершила гармоническое колебательное движение, действующая на нее сила должна быть прямо пропорциональна величине ее смещения х и направлена в сторону, противоположную этому смещению.
Так как в формуле (10) величины m и w являются постоянными, их произведение можно представить в виде постоянного коэффициента к:
 (11)
(11)
а силу, вызывающую гармоническое колебание (10) можно записать
 (12)
(12)
где к - жесткость или коэффициент упругости, который численно равен силе, вызывающей смещение материальной точней на единицу длины.
Сила, определяемая соотношением (12) прямо пропорциональна величине х смещения частицы из положения равновесия и направлена в сторону, противоположную направлению смещения (на что указывает знак минус), называется квазиупругой силой. Квазиупругая сила является силой возвращающей.
В случае, когда на колеблющуюся систему не действуют внешние переменные силы и силы трения, ее собственные колебания называются свободными незатухающими гармоническими колебаниями.
Они характеризуются постоянной амплитудой и могут продолжаться сколь угодно долго.
Уравнение, описывающее свободные незатухающие колебания легко получить из (4), представив ускорение как

и зная, что гармонические колебания вызываются действием квазиупругих сил (12)
 (13)
(13)
Перенеся все члены уравнения (13) в одну сторону, разделив их на m и используя формулу (11), получим
 (14)
(14)
Примечание: В физике принято обозначать циклическую частоту незатухающих колебаний w0, а циклическую частоту затухающих колебаний w.
Тогда, согласно (12)
 (15)
(15)
а период свободных незатухающих гармонических колебаний с учетом (3)
 (16)
(16)
Решение уравнения (14), определяющее смещение при свободных незатухающих колебаниях, будет иметь вид (4) (с учетом w=w0).
График соответствующего движения показан на рис.1.
ФИЗИЧЕСКИЙ МАЯТНИК
В физике под маятником понимают твердое тело, совершающее под действием вращающего момента силы тяжести колебания вокруг неподвижной точки или оси. Для общности рассмотрим в качестве маятника произвольное твердое тело, закрепленное в точке О, как показано на рис.2. Сила тяжести  приложена в центре тяжести, совпадающем о центром масс в точке О'.Физический маятник удобнее всего изучать о помощью уравнений динамики вращательного движения. Момент силы, действующей на физический маятник относительно точки О определяется выражением
приложена в центре тяжести, совпадающем о центром масс в точке О'.Физический маятник удобнее всего изучать о помощью уравнений динамики вращательного движения. Момент силы, действующей на физический маятник относительно точки О определяется выражением
 (17)
(17)

|
Знак "-" обусловлен тем, что направления векторов  и
и  , определяемые правилом правого винта противоположны.
, определяемые правилом правого винта противоположны.
Считая направление положительным, для проекции на это направление получаем выражение (17). Этот момент силы является результирующим и согласно основному уравнению динамики вращательного движения имеем

где  -угловое ускорение, J - момент инерции тела.
-угловое ускорение, J - момент инерции тела.
Отсюда:
 (18)
(18)
Для малых колебаний
 (19)
(19)
Отсюда
 (20)
(20)
Решением уравнения (20) является временная зависимость углового смещения

Обозначим коэффициент при j во втором слагаемом уравнения (20) через w2 , т.е. с учетом  , получим
, получим
 (21)
(21)
Период собственных свободных гармонических колебаний физического маятника будет равен с учетом (21)
 или
или  (22)
(22)
Из сравнения формулы (22) для периода свободных гармонических колебаний физического маятника с формулой
 (23)
(23)
для периода таких же колебаний математического маятника, видно, что периоды их колебаний будут одинаковы при следующем условии:
 (24)
(24)
Величина  называется приведенной длиной физического маятника. Другими словами приведенной длиной физического маятника называют длину такого воображаемого математического маятника, который имеет период колебаний, одинаковый с периодом данного физического маятника.
называется приведенной длиной физического маятника. Другими словами приведенной длиной физического маятника называют длину такого воображаемого математического маятника, который имеет период колебаний, одинаковый с периодом данного физического маятника.
Соотношение (22) применимо для определения момента инерции твердого тела методом обращения этого тела в физический маятник:
 (26)
(26)
где  - период колебаний физического маятника,
- период колебаний физического маятника,
 - масса маятника,
- масса маятника,
 - расстояние между осью вращения и осью, проходящей через центр тяжести тела.
- расстояние между осью вращения и осью, проходящей через центр тяжести тела.
Кроме того, известно, что момент инерции относительно произвольной оси вращения находится по теореме Штейнера:
 (27)
(27)
которая утверждает, что момент инерции тела J относительно произвольной оси вращения равен сумме момента инерции JC относительно оси, проходящей через центр тяжести, и произведения массы тела m на квадрат расстояния d между этими осями.