Переход от исходного распределения к условному

Цель работы

Найти оценки параметров случайной величины Х по данным выборочной совокупности (статистической совокупности). В предположении, что закон распределения случайной величины Х – нормальный, построить кривую плотности. Проверить гипотезу нормальности распределения по критерию Пирсона.

Пояснения к работе

Для исследования случайной величины Х проведено n независимых испытаний, в результате которых получена статистическая, или выборочная совокупность (выборка) объёма n. Значения элементов выборки представляют собой последовательность

, (1)

среди членов которой могут быть и повторяющиеся.

Работу можно разделить на три этапа.

Переход от исходного распределения к условному

Если объём статистической совокупности n ³ 40, то все множество значений выборки (1) разбивается на классы. Число классов k определяется по объему выборки n с помощью табл. 1.

Т а б л и ц а 1

Объём выборки n	40 – 60	60 – 100	100 – 200	200 – 500
Число классов k	6 – 7	7 – 10	10 – 14	14 – 17

Из множества значений (1) выбирают наибольшее x_max и наименьшее x_min значения и определяют длину классового промежутка D по формуле

. (2)

Значение D берется приближенно с той же точностью, с которой определены значения элементов выборки (1). Желательно, чтобы последняя цифра значения величины D была четной. Приведенное округление не сказывается на основном результате, но фактическое число классов может несколько отличаться от выбранного значения k. Чтобы оно соответствовало табл. 1, рекомендуется при первоначальном выборе k не брать крайних значений, приведенных в табл. 1.

Границы классовых промежутков определяются следующим образом: левая граница первого промежутка принимается равной 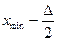. Левая граница каждого следующего промежутка получается прибавлением D к левой границе предыдущего промежутка. Правый конец каждого промежутка меньше левого конца следующего промежутка на единицу последнего десятичного разряда значений в совокупности (1). Этим обеспечивается то, что каждое значение выборки попадает только в один интервал. Границы промежутков вносятся в столб. 1. табл. 2.

Т а б л и ц а 2

Границы промежутков. от и до	Сере- дины проме-жутков	Штрихо- вание	Частоты Z	Условные значения a	aZ	a²Z	a³Z	a⁴Z

		## ## //
Сумма

Все элементы выборки (1) должны относиться к тому или иному классовому промежутку. При этом все элементы, попавшие в один и тот же промежуток, считаются равными между собой и равными среднему арифметическому границ промежутка. Эти значения вносятся во второй столбец табл. 2 и обозначаются . Отметим, что достаточно найти середину только одного из классовых промежутков, так как середины соседних промежутков отличаются друг от друга на D. Теперь вместо исходной выборки (1) изучается ее приближение, выборочный ряд .

Пример. Исследовать случайную величину X – прочность (разрывная нагрузка), мН, пряжи линейной плотности 18,5 текс. Для этого произведена выборка объема n = 40.

Результаты испытаний приведены ниже.

144, 149, 199, 174, 176, 183, 239, 208,

120, 150, 203, 160, 180, 207, 221, 220,

117, 158, 170, 282, 177, 218, 210, 190,

225, 149, 250, 101, 179, 236, 198, 193,

230, 240, 163, 238, 178, 183, 213, 211.

Находим x_min = 101; x_max = 282. Для n = 40 из табл. 1 выбираем k = 6. Тогда длина классового промежутка

Составляем табл. 3 по форме табл. 2.

Т а б л и ц а 3

			a_i	a_iZ_i
86 – 115 116 – 145 146 – 175 176 – 205 206 – 235 236 – 265 266 – 295	100,5 130,5 160,5 190,5 220,5 250,5 280,5	/ /// ## /// ## ## // ## ## ## /	-3 -2 -1	-3 -6 -8	-27 -24 -8
Сумма

Левая граница 1-го интервала . Далее 86 + 30 = 116; 116 + 30 = 140 и т. д. Правая граница первого интервала 116 - 1=115, следующая – 115 + 30 = 145 и т.д. Затем заполняем второй столбец , и т.д. Эти значения внесены в столбец 2 табл.3.

Вернёмся к табл. 2. После того как заполнены столбец 1 и 2 табл. 2, переходят к столбцу 3. Для каждого элемента выборки (1) находят классовый промежуток, которому принадлежит этот элемент, и в строке этого промежутка в столб. 3 ставят штрих. Рекомендуется четыре штриха ставить вертикально, а пятый – горизонтально, перечеркивая им четыре предыдущих. Сумма штрихов в ячейке равна частоте соответствующего значения и записывается рядом (в столб. 4). Частоты обозначаются и их сумма ставится в последней строке. При этом должно выполнятся условие .

Пример (продолжение) По приведенному правилу были заполнены столб. 3 и 4 табл. 3.

Выбираем условный нуль А, совпадающий с тем значением x_i , которое соответствует среднему классовому промежутку, а если таковых два, то тому из них, который имеет большую частоту Z_i.

Для удобства дальнейших вычислений вводятся условные значения a_i:

, (3)

где a_i - i-е условное значение;

x_i – середина i-го классового промежутка;

А – условный нуль.

Заметим, что вычислений по формуле (3) можно не проводить, так как строке табл. 2, соответствующей условному нулю А, соответствует a_i = 0, строки над этой имеют соответственно a_i_-1= - 1, a_i_-2= - 2, и т. д., а строки под i-й - a_i₊₁= 1, a_i₊₂= 2, a_i₊₃= 3 и т.д. После этого заполняются столбцы 6 - 9, а затем последняя строка – «Сумма» – для этих столбцов.

Пример (продолжение). В табл. 3 условный нуль соответствует среднему интервалу с наибольшей частотой . Поэтому .

Далее ⇒