Машинный нуль, машинная бесконечность, машинный эпсилон

Далее ⇒

ЛАБОРАТОРНАЯ РАБОТА 1.

ТЕОРИЯ ПОГРЕШНОСТЕЙ И МАШИННАЯ AРИФМЕТИКА

Цель: сформировать навыки решения задач на вычислительные погрешности.

Основные теоретические сведения

Абсолютная и относительная погрешность

Определение. Приближенным числом называется число, незначительно отличающееся от точного числа и заменяющее последнее в вычислениях.

Математическая запись

Определение. Под абсолютной погрешностью Δ приближенного числа понимается разность

Отсюда следует, что заключено в пределах

или

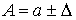
Определение. Относительной погрешностью приближенного числа называется отношение абсолютной погрешности этого числа к модулю соответствующего точного числа

Так как обычно неизвестно, то на практике применяют оценку

Верные цифры числа

Всякое положительное число может быть представлено в виде конечной или бесконечной десятичной дроби

где - цифра числа в i – м разряде, m – старший десятичный разряд числа.

Пример:

Определение. Значащей цифрой приближенного числа называется всякая цифра в его десятичном представлении, отличная от нуля, и нуль, если он содержится между значащими цифраи или является представителем сохраненного десятичного разряда.

Пример. = 0.002080. Здесь только первые три нуля не являются значащими.

Определение. n первых значащих цифр приближенного числа являются верными, если абсолютная погрешность этого числа не превышает половины разряда, выражаемого n – й значащей цифрой, считая слева направо. Цифры, не являющиеся верными, называются сомнительными

Пример. Если в числе = 0.03450 все цифры верные, то .

Таким образом, если для приближенного числа известно, что

то, по определению, первые n цифр этого числа являются верными.

Пример. , . Тогда

Т.е. m-n+1=-1. Т.к. m = 1, то n = 3. Следовательно, приближенное число имеет 3 верных цифры и его следует округлить следующим образом:

Связь относительной погрешности с количеством верных знаков числа

Если положительное приближенное число имеет относительную погрешность , то количество верных знаков n данного числа можно определить по формуле

и в качестве n взять ближайшее целое к число.

Погрешности арифметических действий

Общая формула вычисления погрешности

Машинный нуль, машинная бесконечность, машинный эпсилон.

В ЭВМ для вещественных чисел используется двоичная система счисления и принята форма представления чисел с плавающей точкой , . Здесь - мантисса; - двоичные цифры, причем всегда =1, p-целое число называемое двоичным порядком. Количество t цифр, которое отводится для записи мантиссы, называется разрядностью мантиссы. Диапазон представления чисел в ЭВМ ограничен конечной разрядностью мантиссы и значением числа p. Все представимые числа на ЭВМ удовлетворяют неравенствам: , где , . Все числа, по модулю большие , не представимы на ЭВМ и рассматриваются как машинная бесконечность. Все числа, по модулю меньшие , для ЭВМ не отличаются от нуля и рассматриваются как машинный нуль. Машинным эпсилон называется относительная точность ЭВМ, то есть граница относительной погрешности представления чисел в ЭВМ. Покажем, что . Пусть , тогда граница абсолютной погрешности представления этого числа равна . Поскольку , то величина относительной погрешности представления оценивается так:

Машинное эпсилон определяется разрядностью мантиссы и способом округления чисел, реализованным на конкретной ЭВМ.

Примем следующие способы определения приближенных значений параметров, требуемых в задаче:

1. Положим , где n - первое натуральное число, при котором происходит переполнение.

2. Положим , где m – первое натуральное число , при котором совпадает с нулем.

3. Положим , где k – наибольшее натуральное число, при котором сумма вычисленного значения 1+ еще больше 1. Фактически есть граница относительной погрешности представления числа .

Результаты вычислительного эксперимента:

Машинная бесконечность

Машинный нуль

Машинное эпсилон

Индивидуальные задания

Задача 1. Дан ряд (см. ПРИЛОЖЕНИЕ 1). Найти сумму ряда аналитически. Вычислить значения частичных сумм ряда и найти величину погрешности при значениях N=10, 10², 10³, 10⁴, 10⁵.

ПОРЯДОК РЕШЕНИЯ ЗАДАЧИ (Пример приведен в ПРИЛОЖЕНИИ 2).

1. Найти сумму ряда S аналитически как предел частичных сумм ряда (см. ПРИЛОЖЕНИЕ 2) или с использованием средств MATHCAD.

2. Используя функцию , вычислить значения частичных сумм ряда при указанных значениях N.

3. Для каждого N вычислить величину абсолютной погрешности , относительную погрешность d и определить количество верных цифр в S(N)

4. Представить результаты в виде гистограмм.

Задача 2 . Дана функция f(a,b,c) (см. ПРИЛОЖЕНИЕ 1). Значения переменных указаны в варианте со всеми верными цифрами. Оценить погрешность результата, используя: a) оценки погрешностей для арифметических операций; b) общую формулу погрешностей. Результат представить в двух формах записи: с явным указанием погрешностей и с учетом верных цифр.

Задача 3. Для пакета MATHCAD найти значения машинного нуля, машинной бесконечности, машинного эпсилон (см. ПРИЛОЖЕНИЕ 3).

Контрольные вопросы

1. Введите определения приближенного числа, абсолютной и относительной погрешности.

2. Какие цифры для заданного приближенного числа являются значащими? Приведите примеры.

3. Какие цифры для заданного приближенного числа являются верными? Приведите примеры.

4. Какие цифры для заданного приближенного числа являются сомнительными? Приведите примеры.

5. Обозначьте связь относительной погрешности с количеством верных знаков числа

6. Как определяется погрешность арифметических действий?

7. Объясните общую формулу вычисления погрешности.

8. Опишите форму представления чисел в ЭВМ

9. Введите определения машинной бесконечности, машинного эпсилона, границы относительной погрешности. Опишите способы их определения.

10. Как оценивается величина относительной погрешности?

ПРИЛОЖЕНИЕ 1

ВАРИАНТЫ ЗАДАНИЙ К ЛАБОРАТОРНОЙ РАБОТЕ 1

Таблица к задаче 1

N	N	N








		29

Таблица к задаче 2

№				№
	0.0125	0.283	0.0187		4.41	18.5
	14.29	13.81	10.98		16.5	4.2
	12.28	13.21	12.19		52.31	48.95	47.81
	0.328	0.781	0.0129		4.81	4.52	9.28
	14.85	15.49			16.21	16.18	21.23
	12.31	0.0352	10.82			0.324	1.25
	12.45	11.98			25.18	24.98
	3.456	0.642	7.12		3.1415	3.1411	10.91
	1.245	0.121	2.34		3.14	1.57	0.0921
	13.12	0.145	15.18		14.85	15.49
	0.643	2.17	5.843		5.325	5.152	5.481
	0.3575	2.63	0.854		71.4	4.82	49.5
	14.91	0.485	14.18		4.356	4.32	0.246
	16.5	4.12	0.198		3.42	5.124	0.221
	5.21	14.9	0.295		0.5761	3.622	0.0685

ПРИЛОЖЕНИЕ 2

Далее ⇒