Математическая формулировка задачи. Цель работы – исследовать эффективность алгоритмов трассировки проводных соединений методом «внавал»; освоить особенности алгоритмизации и программирования

ЛАБОРАТОРНАЯ РАБОТА № 5

ИССЛЕДОВАНИЕ ЭФФЕКТИВНОСТИ АЛГОРИТМОВ

ТРАССИРОВКИ ПРОВОДНЫХ СОЕДИНЕНИЙ

Цель работы – исследовать эффективность алгоритмов трассировки проводных соединений методом «внавал»; освоить особенности алгоритмизации и программирования задачи трассировки проводов на ПЭВМ; приобрести навыки построения математических моделей проводных соединений, реализации и исследования их при решении задачи трассировки с применением САПР.

АЛГОРИТМЫ ТРАССИРОВКИ ПРОВОДОВ

Задача проектирования соединений, иначе трассировка соединений, возника-ет на последних этапах проектирования радиоэлектронных средств (РЭС) и является одной из наиболее сложных задач в общей проблеме автоматизации проектирования РЭС [1-5]. Связано это с многообразием способов конструк-торско-технологической реализации соединений, каждый из которых обусловливает использование специфических критериев оптимизации и ограни-чений при алгоритмическом решении этой задачи.

Проводной монтаж, несмотря на широкое применение печатного монтажа, занимает значительное место в современных РЭС. Он более прост, т. к. проводники изолированы друг от друга, не надо думать об ограничениях на пересечения проводов, поэтому достаточно минимизировать длину соединений. В серийном производстве проводные соединения используют в узлах, платах, субблоках, кассетах, блоках, рамах, шкафах.

В современных РЭС трассировку проводных соединений производят двумя способами [1-2]:

– по прямым, соединяющим отдельные выводы модулей (монтаж «внавал»);

– по ортогональным направлениям – с помощью жгутов.

Достоинство монтажа «внавал»: простота при выполнении и высокая помехоустойчивость, т. к. он позволяет сократить до минимума общую длину проводников и протяженность участков их параллельного прохождения.

Недостатки: при его исполнении высока вероятность появления ошибок, которые трудно обнаружить, и из-за высокой плотности монтажа этот способ обладает малой ремонтопригодностью.

При жгутовом монтаже проводники объединяются в жгуты (перевязанные прочной нитью проводники), которые укладываются в специальные каналы.

Достоинство жгутового монтажа: более технологичен, т. к. позволяет разделить операции вязки и распайки жгутов, а также упростить процесс контроля и устранения ошибок, допущенных при монтаже.

Недостатки: неприемлем при создании высокочастотной и чувствительной к электрическим помехам аппаратуре. Основные ограничения при проводном монтаже – количество проводников, которые можно подсоединить к одному выводу (обычно не более трех) и число проводов в каждом жгуте.

Теоретически к одному выводу может быть подсоединено не более шести проводников. Это легко понять из чертежа, представленного на рис.1. Допус-тим, точки a₁, a₂, …, a_n удалены от точки О на расстояние R. Тогда можно считать, что эти точки расположены на окружности с радиусом R (рис.1, а). Из геометрии известно, что в круг вписывается правильный шестиугольник со стороной, равной радиусу круга (рис.1, б). Очевидно, что в данном случае ми-нимальное дерево в вершинах O, a₁, a₂, a₃, a₄, a₅, a₆ только шестиугольника имеет суммарную длину ребер, равную 6R (рис.1, в, г). Причем максимальную локальную степень = 6 будет иметь вершина O в звездном варианте такого дерева (рис.1, в). Любая дополнительная вершина a₇ на расстоянии R от вершины O будет уже ближе к одной из точек a_i (рис.1, д, е). Поэтому _max = 6.

Математическая формулировка задачи

В общем виде задача формулируется следующим образом [2]. В системе координат XYZ, связанной с коммутационным пространством модуля, задано местоположение множества выводов . Это множество M разобьем в соответствии с электрической схемой соединений на непере-секающиеся подмножества M⁽¹⁾, M⁽²⁾,…,M⁽^k⁾, каждое из которых включает в себя выводы, подлежащие электрическому объединению. 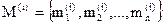Для каждого подмножества , i = 1, 2, …, k требуется определить последовательность соединений выводов и конфигурацию проводников, обеспечивающих при заданных ограничениях минимальную суммарную длину соединений.

Практически задача сводится к отысканию дерева с минимальной суммарной длиной ребер (построению кратчайшей связывающей сети). Согласно теореме Кэли на n вершинах может быть построено t = n⁽ⁿ^-2) деревьев. Поэтому при большом числе выводов в электрической цепи эта задача становится сложной.

Для определения минимального дерева на заданных n вершинах можно построить все возможные деревья и выбрать минимальное из них. Однако в РЭC число цепей исчисляется сотнями, поэтому поиск всех деревьев практи-чески нереален. К тому же существующие алгоритмы построения минимальных деревьев позволяют находить глобально-оптимальные или близкие к ним решения (при отсутствии ограничений на количество проводников, подсоединяемых к одному выводу). Поэтому эта задача является одной из немногих задач теории графов, которые считают полностью решенными [8]. Рассмотрим используемые в САПР алгоритмы Дж. Краскала и Р. К. Прима.

Алгоритм Краскала

Алгоритм Краскала реализует следующую процедуру [1, 2, 9].

Множество контактов n электрической цепи моделируют n вершин графа. На них строится полный граф. Число ребер в полном графе r = [n (n-1) / 2]. Из списка ребер полного графа последовательно выбираются самые короткие ребра до тех пор, пока не получится дерево.

Особенностью этого алгоритма является возможность параллельного образования нескольких поддеревьев, которые затем объединяются в единое дерево – остов.

При этом очередное выбранное ребро включается в список выбранных ре-бер в том случае, если оно не инцидентно сразу двум вершинам любого из уже построенных ранее фрагментов. Иначе ребро исключается, поскольку при его добавлении к фрагменту образовался бы простой цикл. Процедура выбора ре-бер продолжается до тех пор, пока в списке ребер дерева не окажется ровно

( n – 1 ) ребер.

Выбор ребра минимальной длины сводится к поиску минимального эле-мента в одной из половинок матрицы расстояний с последующим присвоением этому элементу значения, превышающего все остальные элемен-ты (например, ) для исключения повторного его выбора. Если при построе-нии дерева в полном графе оказывается несколько рёбер одинаковой минималь-ной длины, то для нахождения глобально-оптимального решения необходимо построить деревья с каждым из таких ребер и выбрать минимальное из них.

Проверка ребра на образование цикла выполняется с помощью таблицы меток вершин N_i, где i = 1, 2, …, n. В начале работы алгоритма в этой таблице все вершины имеют разные метки (например, свой номер N_i = i). Если две изолированные i и j вершины объединяются во фрагмент, то происходит поглощение меток: N_i присваивается значение N_j или наоборот. Аналогично обстоит дело и при образовании более сложных фрагментов: если два фраг-мента объединяются ребром r_ij в один, то все метки вершин получают одинако-вое значение N_i, обычно минимальное из сравниваемых. По таблице меток легко проверить, образует ли очередное выбранное ребро цикл или нет: цикл образуется в том случае, если соединяемые вершины имеют одинаковые метки.

Алгоритм позволяет строить дерево и с ограничениями на степени вершин, однако в этом случае получение минимального дерева не гарантируется.

Рис. 5.1.

Если локальные степени вершин не должны превышать двух, то задача построения минимального дерева сводится к задаче построения гамильтоновой цепи минимальной длины: пройти по всем вершинам графа, но не возвращаться в исходную вершину [6 – 9].

В алгоритмах проверка ограничений на степени вершин осуществляется каждый раз при выборе очередного минимального ребра, и если присоединение этого ребра увеличивает степень некоторой вершины m_i фрагмента более чем это допустимо, то такое ребро отбрасывается.

АЛГОРИТМ

1. На множестве вершин (выводов) M⁽ⁱ⁾ построить взвешенный полный граф (число ребер в нем n(n-1)/2). Для этого вычислить элементы матрицы расстояний по одной из формул:

или (5.1)

, (5.2)

где и – координаты i-й и j-й позиций монтажного пространства.

Формулой (5.1) пользуются для монтажа «внавал», а формулой (5.2) – при жгутовом монтаже.

2. Всем элементам, лежащим на главной диагонали и ниже её, присваивается значение . Присвоить нулевое значение длине L рёбер искомого дерева: L = 0; i = 0; j = 0.

3. Сформировать таблицу меток и локальных степеней вершин: ; ; ; ; .

4. Присвоить .

5. Найти минимальный элемент матрицы .

6. Если , то идти к 4.

7. Если или , то идти к 4.

8. Поглощение меток: все метки нового фрагмента получают значение , а локальные степени соединенных вершин – и .

9. Включить ребро во множество R ребер минимального дерева, а длину дерева увеличить на длину ребра: .

10. Если , то идти к 4, в противном случае к 11.

11. Минимальное дерево построено. R – множество его ребер, а L – суммарная их длина.

Конец.

ПРИМЕР 5.1

На плоскости в декартовой системе координат задано местоположение шести точек (рис. 5.2.). Расстояние между любыми двумя точками и определено по формуле (5.1). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин не должны превышать двух – .

Решение

Составляем матрицу длин и всем элементам, лежащим на главной диагонали и ниже нее, присваиваем значение :

D=
	1,4		4,5	6,3
		3,2	4,2	5,1	6,1
				2,8
			4,5	3,6
					2,2

Формируем таблицу меток и локальных степеней (см. табл. 5.1).

На нулевом шаге все вершины получают метки, равные их номерам , а локальные степени , , длина строящегося дерева и множество ребер в дереве êR ê= Æ.

На первом шаге просматриваем элементы верхней половины матрицы D и выбираем из них минимальный элемент (при наличии нескольких элементов с одинаковыми минимальными значениями выбираем элемент с наименьшими индексами i и j).

Таблица 5.1.

Номер вершины	Значения меток и степеней вершин на очередном шаге









		1,4	3,4	5,6	8,4	8,4	6,4	8,4	8,4	12,6

Помечаем элемент и на его место записываем . Метки у 1-й и 2-й вершин разные ( , ), поэтому соединяем вершины 1-ю и 2-ю ребром: метки у них становятся равными: . Локальные степени обеих вершин равны единицам – и .

Рис. 5.2.

Рис.5.3.

Длина L строящегося дерева равна 1.4, а множество ребер êR ê = 1 (см. 1-й шаг табл. 1). На втором шаге выбирается минимальный элемент , на третьем – , на четвертом – (см. рис. 5.2). На места выбранных элементов в матрице D записываем . Получили матрицу D₁:

D₁=
		4,5	6,3
	3,2	4,2	5,1	6,1

		4,5	3,6

В выделяемом минимальном дереве построены два фрагмента с суммарной длиной . У вершин 1-го фрагмента (1-й и 2-й) метки и локальные степени . У вершин 2-го фрагмента (3-й, 4-й, 5-й, 6-й) метки , а локальные степени - , .

Выбранный из оставшихся минимальный элемент , на очередном 5-м шаге, не может быть включен во множество R ребер дерева, поскольку образует цикл с ребрами ранее построенного фрагмента (на это указывают одинаковые метки у 3-й и 6-й вершин ).

На шестом и восьмом шагах выбранные ребра и соот-ветственно не образуют циклов, но их присоединение нарушает ограничение на локальную степень 3-й вершины. На седьмом – ребро не может быть подсоединено вновь из-за образования цикла (рис. 5.3).

На девятом шаге присоединяется ребро , при этом выполняется условие , т. е. дерево построено: , длина дерева (рис. 5.4). Если бы ограничение на степени вершин отсутство-вало, то можно было бы построить дерево с меньшей длиной (рис. 5.4).

Рис. 5.4.

Алгоритм Прима

Алгоритм Прима реализует следующую процедуру [1 – 7].

На каждом шаге просматриваются только те ребра графа, которые связы-вают вершины строящегося поддерева с новыми, еще не присоединенными вершинами, т.е. ищется вершина, ближайшая от всего построенного фрагмента дерева. Отсюда, в отличие от алгоритма Краскала, единственное строящееся поддерево последовательно наращивается до построения остова.

Основные принципы построения минимального связывающего дерева (или кратчайшей связывающей сети) при наличии ограничений на локальные степени вершин следующие.

В начале любая произвольная вершина соединяется с ближайшей соседней, образуя исходное поддерево. (Для определенности построения мини-мального дерева можно начинать с ребра, инцидентного первой вершине , или с минимального ребра). На каждом последующем шаге к строящемуся поддереву присоединяют очередное ребро минимально возможной длины, связывающее новую, еще не присоединенную вершину с одной из вершин поддеревьев , локальная степень которой .

Для реализации алгоритма составляют матрицу расстояний , элемент которой вычисляют по одной из формул (5.1) или (5.2). Просматривают элементы первой строки матрицы D и находят минимальный элемент. Пусть таким оказался элемент g-го столбца, тогда весь 1-й и g-й столбцы матрицы D исключаются из рассмотрения, а первое соединение проводится между точками и . Просматриваются 1-я и g-я строки матрицы с оставшимися элементами. Из элементов этих строк находится минимальный. Предположим, что им оказался элемент, принадлежащий j-му столбцу. Если этот элемент находится на пересечении с первой строкой, то точку соединяем с 1-й точкой ( ), если же он находится на пересечении с g-й строкой, то точку соединяем с g-й ( ), после чего из матрицы D исключаем все элементы j-го столбца. Просматриваются 1-я, g-я и j-я строки и т. д.

Выполнение ограничения на локальную степень вершин обеспе-чивается проверкой в каждой просматриваемой i-ой строке числа уже выбранных для построения минимального дерева элементов – . При все оставшиеся элементы i-й строки исключаются из рассмотрения, т.е. эта строка удаляется.

АЛГОРИТМ

1. Вычислить элементы матрицы расстояний по одной из формул – (5.1) или (5.2).

2. Найти минимальный элемент матрицы , где ; . Номера строки и столбца q и p, на пересечении которых он находится, определяют номера вершин и , соединяемых ребром.

3. Занести номера вершин во множество , построенное ребро – во множество .

4. Подсчитать локальные степени и , подлежащих соединению на данном шаге вершин и .

5. Проверить условие и . Индексы вершин, для которых это условие не выполняется, указывают номера строк матрицы D, которые необходимо исключить из рассмотрения.

6. Найти . Здесь , , т. е. среди еще не вошедших в дерево вершин отыскать вершину , минимально удаленную от некоторой вершины дерева .

7. Дополнить множества ; .

8. Проверить, все ли вершины графа соединены ветвями . Если условие выполняется, идти к 9, иначе – к 4.

Конец.

ПРИМЕР 5.2

На плоскости в декартовой системе координат задано местоположение шес-ти точек (рис. 5.5). Расстояние между любыми двумя точками и определено по формуле (5.2). Требуется для заданного множества точек M определить минимальное связывающее дерево при условии, что локальные степени вершин не должны превышать двух: .

Решение

Составляем матрицу расстояний

D=
							1+1

Просматриваем все строки матрицы и выбираем элемент, являющийся минимальным. Поскольку таких элементов два , выбираем элемент с наименьшими индексами – . Помечаем его, локальные степени 1-й и 2-й вершин увеличиваем на единицу – . Исключаем из рассмотрения (вычеркиваем) все элементы первого и второго столбцов. Соединяем и (рис. 5.6, а).

Просматриваем первую и вторую строки матрицы. Выбираем элемент ; локальные степени 1-й и 3-й вершин увеличиваем на единицу – ; . Исключаем из рассмотрения элементы 3-го столбца и 1-й строки (к 1-й вершине подключено уже два ребра). Соединяем с (рис. 5.6, б). Получили матрицу D₁:

D₁=

				1+1
				1+1

Просматриваем вторую и третью строки. Выбираем элемент ; ; . Соединяем вершины и (рис. 5.6, в). Исключаем из рассмотрения четвертый столбец и третью строку, поскольку .

Просматриваем вторую и четвертую строки. Выбираем элемент ; ; . Соединяем с (рис. 5.6, г). Поскольку , исключаем из рассмотрения шестой столбец и четвертую строку. И, наконец, просма-триваем вторую и шестую строки. Выбираем ; , . Соединяем с (рис. 5.6, д). Исключаем из рассмотрения последний пятый столбец.

Минимальное связывающее дерево, полученное в результате решения, приведено на рис.5.6, д.

Рис. 5.5

Множество ребер в нем . Суммарная длина его ребер L равна 16.

Если локальную степень вершин не ограничивать, то в результате решения будут выбраны элементы , , , , и суммарная длина ребер при этом равна 14 (см. рис. 5.6, е).

Выводы: Оба рассмотренных алгоритма позволяют при выполнении соот-ветствующих условий находить глобально-оптимальные или близкие к ним решения.

При этом для работы алгоритма Краскала требуется n (n-1)/2 памяти ЭВМ для записи исходных данных, однако в процессе работы необходимо дополни-тельное время для проверки ребер на образование циклов.

Для работы алгоритма Прима памяти необходимо n², но зато отсутствует необходимость проверки ребер на образование циклов.

Следовательно, алгоритм Краскала требует в два с лишним раза меньше памяти, чем алгоритм Прима; зато машинного времени меньше необходимо при расчёте по алгоритму Прима. Кроме этого надо отметить, что алгоритм Краскала более прост при реализации.

ДОМАШНЕЕ ЗАДАНИЕ

2.1. Ознакомиться с алгоритмами решения задачи трассировки проводных соединений методом «внавал».

2.2. Изучить алгоритмы трассировки Р. К. Прима и Дж. Краскала.

2.3. Подготовить данные к эксперименту.

2.4. Выполнить расчёты по трассировке проводов в заданных узлах алгорит-мами Р. К. Прима и Дж. Краскала.

Рис.5.6.

ЗАДАНИЕ К ЛАБОРАТОРНОЙ РАБОТЕ

3.1. Порядок работы с программой «PCPROV»

Алгоритмы трассировки проводных соединений методом «внавал» реализованы в пакете учебной САПР PSAPRна ПЭВМ программой «Трассировка проводов». Программа позволяет:

- определять соединения минимальной длины для множества контактов отдельных электрических цепей;

- при нахождении соединений минимальной длины учитывать конструктив-ные и технологические ограничения на количество проводов, подводимых к отдельным контактам.

- определять суммарную длину соединений построенной электрической цепи;

Для запуска программы «Трассировка проводов» установить курсор на окно с этим названием (оно будет в зелёной рамке) и нажать Enter. Появится рабочее поле графического редактора «Трассировка проводов» (рис.5.7).

В верхней части экрана дано название программы и включённый режим.

В центральной части экрана размещено дискретное рабочее поле, на котором набираются точки (контакты) электрической цепи. Для их ввода надо установить курсор в нужное место экрана и нажать клавишу Insert. На поле

Рис.5.7.

появится красная точка. Таким образом ввести все контакты одной цепи (рис.5.8).

Справка о работе программы выводится на экран после нажатия клавиши F1 – Помощь (см. рис.5.8).

Рис.5.8

В нижней части экрана размещена строка с указаниями алгоритма, типа трассировки и локальной степени вершин. Последней выведена строка с указаниями клавиш и названий основных команд редактора.

После того как все контакты цепи введены, можно приступать к решению задачи трассировки. Для этого нажатием клавиши Enter можно по шагам выполнить весь расчёт. На экране, на каждом шаге будут строиться соединения между отдельными точками до тех пор, пока не будет построено дерево (рис.5.9).

Выбор соединений по прямым – «внатяг» и уменьшение локальной степени вершин приводит к изменению вида рисунка дерева (рис. 5.10).

Экспериментальная часть

3.1. Запустить программу «Трассировка проводов».

3.2. Получить у преподавателя технические условия на проектирование проводного монтажа. На дискретном рабочем поле с помощью графического редактора задать контакты электрической цепи.

3.3. Выбрать алгоритм Прима, трассировку «внатяг» и локальную степень равную 6.

Рис.5.9.

3.4. Выполнить трассировку в этом режиме. Зафиксировать результат трассировки.

3.5. Установить локальную степень равной 2 и построить гамильтонову цепь.

3.6. Переключить на режим ортогональной трассировки и выполнить расчет по программе вначале с локальной степенью 6, а затем 2.

3.7. После этого выбрать алгоритм Краскала и выполнить аналогичные расчёты для ортогональной трассировки и трассировки «внатяг».

3.8. Сравнить результаты трассировок и выбрать лучший результат. Оценить возможность ручной доработки результата.

3.9. Записать результаты трассировок на диск.

3.10. Начертить эскизы трассировок цепи разными алгоритмами и при различных условиях.

3.11. Оценить результаты трассировки проводов по всем критериям и проанализировать возможность «ручной» доработки полученного результата или повторного решения с уточненными требованиями к трассировке.

Для заданных электрических соединений и монтажного пространства составить математические модели необходимые для расчетов по алгоритмам Прима и Краскала.

3.12. По обоим алгоритмам рассчитать вручную минимальные деревья.

3.13. Оценить эффективность исследуемых алгоритмов трассировки проводов с точки зрения требований к математическому обеспечению САПР.

Рис.5.10.

СОДЕРЖАНИЕ ОТЧЕТА

4.1. Цель работы.

4.2. Сведения из теории. Задача трассировки проводов и ее математическая формулировка.

4.3. Графическое изображение на плоскости в декартовой системе координат множества контактов, подлежащих соединению.

4.4. Математические модели электрической цепи, необходимые для расчетов по алгоритмам Прима и Краскала.

4.5. Условия трассировки проводов.

4.6. Распечатки (эскизы) результатов проектирования проводного монтажа по алгоритмам на ПЭВМ.

4.7. Результаты ручного расчета (решения) задачи трассировки проводов по алгоритмам.

4.8. Выводы.

КОНТРОЛЬНЫЕ ВОПРОСЫ

5.1. Назовите и охарактеризуйте виды проводного монтажа, применяемого в современных РЭС.

5.2. Как математически формулируется задача трассировки проводных соединений?

5.3. При каких условиях задача трассировки сводится к построению минимальных связывающего дерева или гамильтоновой цепи?

5.3. Назовите алгоритмы трассировки проводов и в чем их основное различие?

5.4. Каким образом можно оценить качество проводного монтажа?

5.5. Перечислите последовательность действий алгоритма Прима.

5.6. Перечислите последовательность действий алгоритма Краскала.

5.7. Назовите достоинства и недостатки алгоритмов Прима и Краскала, дайте рекомендации по их использованию.

5.8. Поясните порядок работы с программой «Трассировка проводных соединений».

5.9. Как вводятся исходные данные при расчете по программе?