
Категории:
АстрономияБиология
География
Другие языки
Интернет
Информатика
История
Культура
Литература
Логика
Математика
Медицина
Механика
Охрана труда
Педагогика
Политика
Право
Психология
Религия
Риторика
Социология
Спорт
Строительство
Технология
Транспорт
Физика
Философия
Финансы
Химия
Экология
Экономика
Электроника
АЛГОРИТМ ВЫЧИСЛЕНИЯ ПОКАЗАТЕЛЕЙ и экономический анализ полученных результатов
Ленинградский областной институт экономики и финансов
Кафедра высшей математики
ОТЧЕТ
О лабораторной работе № 6
по дисциплине: «Экономико-математические
модели»
на тему: «Модель макроэкономической динамики Харрода-Домара»
(вариант №5)
Гатчина
Содержание
Введение…………………………………………………………………………….3
1. Постановка задачи………………………………………………………4
2. Алгоритм вычисления показателей и экономический анализ полученных результатов…………………………………….10
Заключение……………………………………………………………………...18
Список использованной литературы……………………………...19
Приложение 1……………………………………………………………………20
Приложение 2……………………………………………………………………21
Приложение 3……………………………………………………………………22
Приложение 4……………………………………………………………………23
Приложение 5……………………………………………………………………24
ВВЕДЕНИЕ
Модель макроэкономической динамики Харрода-Домара описывает динамику взаимосвязи основных макроэкономических показателей закрытой экономики.
Данная работа посвящена исследованию динамики дохода при различной динамике потребления в модели Харрода-Домара. В работе необходимо определить принципы формирования структуры выпуска (дохода), распределение его между составляющими, прежде всего – между потреблением и накоплением, а также выявить динамику дохода в зависимости от динамики потребления.
Представленная работа состоит из двух разделов.
В первом разделе делается постановка самой задачи.
Во втором разделе рассматривается алгоритм вычисления показателей и дается экономический анализ полученных результатов.
ПОСТАНОВКА ЗАДАЧИ
Модель макроэкономической динамики Харрода-Домара описывает динамику взаимосвязи основных макроэкономических показателей закрытой экономики. При этом доход 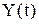 равен сумме объема потребления
равен сумме объема потребления  и инвестиций
и инвестиций  :
:
 . (1)
. (1)
Так как экономика считается закрытой, поэтому чистый экспорт равен нулю и государственные расходы в модели не выделяются. Основное соотношение в модели Харрода-Домара - это взаимосвязь между инвестициями и скоростью роста дохода. Предполагается, что скорость роста дохода пропорциональна инвестициям:
 ,(2)
,(2)
где  – коэффициент приростной капиталоёмкости, или капиталоёмкости прироста дохода, а обратная величина: b=
– коэффициент приростной капиталоёмкости, или капиталоёмкости прироста дохода, а обратная величина: b=  называется приростной капиталоотдачей.
называется приростной капиталоотдачей.
При построении модели приняты следующие допущения:
1. Инвестиционный лаг равен нулю и, следовательно, инвестиции мгновенно переходят в прирост капитала:
 (3)
(3)
где  - непрерывная функция прироста капитала во времени.
- непрерывная функция прироста капитала во времени.
2. Выбытие капитала отсутствует.
3. Производственная функция в модели линейна. Это вытекает из пропорциональности прироста дохода приросту капитала, так как
 ,(4)
,(4)
и, следовательно:  .(5)
.(5)
Однако линейная производственная функция:
 , (6)
, (6)
где  ,
,
обладает этим свойством, если либо  , либо
, либо  . Из данных положений вытекают следующие допущения модели:
. Из данных положений вытекают следующие допущения модели:
1. Затраты труда постоянны во времени либо выпуск не зависит от затрат труда, поскольку труд не является дефицитным ресурсом;
2. Модель не учитывает влияния на объем выпуска продукции научно-технического прогресса.
В модели Харрода-Домара предполагается, что динамика объёма потребления  задаётся экзогенно. Этот показатель может считаться постоянным во времени, расти с заданным постоянным темпом или иметь какую-либо другую динамику
задаётся экзогенно. Этот показатель может считаться постоянным во времени, расти с заданным постоянным темпом или иметь какую-либо другую динамику
1) Простейший вариант модели получается, если считать  . В этом случае все ресурсы экономики направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста дохода и модель, учитывая (1), (2) принимает следующий вид:
. В этом случае все ресурсы экономики направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста дохода и модель, учитывая (1), (2) принимает следующий вид:
 (7)
(7)
Представив (7) в стандартном виде, получим:
 . (8)
. (8)
Выражение (8) – однородное линейное дифференциальное уравнение, решение которого имеет вид:
 . (9)
. (9)
Непрерывный темп прироста равен  . Это максимально возможный (технологический) темп прироста дохода в рассматриваемой экономической системе.
. Это максимально возможный (технологический) темп прироста дохода в рассматриваемой экономической системе.
2) Если  , то получаем:
, то получаем:
 (10)
(10)
или, сделав перестановку членов уравнения, получим:
 . (11)
. (11)
Это - неоднородное линейное дифференциальное уравнение и его частное решение имеет вид: . Складывая частное решение уравнения (11) с общим решением однородного уравнения
. Складывая частное решение уравнения (11) с общим решением однородного уравнения  , получаем его общее решение:
, получаем его общее решение:
 . (12)
. (12)
Подставив в (12)  , получим
, получим  , следовательно, общее решение уравнения (11) будет следующим:
, следовательно, общее решение уравнения (11) будет следующим:
 . (13)
. (13)
Непрерывный темп прироста дохода  для уравнения (11) получим из следующего выражения:
для уравнения (11) получим из следующего выражения:
 . (14)
. (14)
Следовательно, непрерывный темп прироста дохода равен:
 . (15)
. (15)
Он составляет:  в начальный момент времени, при
в начальный момент времени, при  .С ростом времени растет доход Y(t), а потребление С(t) = const. В связи с этим v(t) возрастая, стремится к
.С ростом времени растет доход Y(t), а потребление С(t) = const. В связи с этим v(t) возрастая, стремится к  при
при  , так как доход растёт, а постоянный объём потребления составляет всё меньшую его долю. Величина в скобках:
, так как доход растёт, а постоянный объём потребления составляет всё меньшую его долю. Величина в скобках:
 (16)
(16)
является нормой накопления в момент времени  . Темп прироста дохода пропорционален этой величине, как и показателю приростной капиталоотдачи b.
. Темп прироста дохода пропорционален этой величине, как и показателю приростной капиталоотдачи b.
При прочих равных условиях рост нормы накопления пропорционально увеличивает темпы прироста дохода. Необходимо также отметить, что при C(0) = Y(0) непрерывный темп прироста дохода равен нулю и, следовательно, роста дохода вообще не происходит.
3) При исследовании варианта модели с показателем потребления  , растущим с постоянным темпом
, растущим с постоянным темпом  , т.е.
, т.е.  дифференциальное уравнение модели принимает вид:
дифференциальное уравнение модели принимает вид:
 (17)
(17)
Приведём данное уравнение к стандартному виду:
 . (18)
. (18)
Это - неоднородное линейное дифференциальное уравнение. Решение этого уравнения имеет вид:
 . (19)
. (19)
Согласно экономическому смыслу ясно, что темп прироста потребления  не должен быть больше максимально возможного общего темпа прироста
не должен быть больше максимально возможного общего темпа прироста  . Иначе потребление будет занимать всё большую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход. Это также видно из формулы (19) решения модели. Действительно, если
. Иначе потребление будет занимать всё большую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход. Это также видно из формулы (19) решения модели. Действительно, если  (например,
(например,  ),то коэффициент
),то коэффициент  отрицателен, а
отрицателен, а  растёт быстрее, чем
растёт быстрее, чем  , следовательно, отрицательное второе слагаемое через некоторое время перевесит первое.
, следовательно, отрицательное второе слагаемое через некоторое время перевесит первое.
При  , вид решения в рассматриваемой модели во многом зависит от соотношения между показателями
, вид решения в рассматриваемой модели во многом зависит от соотношения между показателями  и
и  .Величина a - это норма накопления в начальный момент времени
.Величина a - это норма накопления в начальный момент времени  . Значение a определяется по формуле (16):
. Значение a определяется по формуле (16):
 (20)
(20)
Если  , то темп прироста дохода равен темпу прироста потребления. Норма накопления
, то темп прироста дохода равен темпу прироста потребления. Норма накопления  в этом случае постоянна во времени и равна
в этом случае постоянна во времени и равна  , а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоёмкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.
, а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоёмкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.
Если в рассматриваемой модели  , то темп прироста потребления оказывается слишком высоким для экономики. В этом случае коэффициент
, то темп прироста потребления оказывается слишком высоким для экономики. В этом случае коэффициент  в формуле (19) отрицателен, так как
в формуле (19) отрицателен, так как  , и по той же причине первое отрицательное слагаемое с ростом времени превысит второе. Это приводит к тому, что темп прироста дохода падает и становится с некоторого момента отрицательным, а через некоторое время и сам доход становится равным нулю. После этого модель теряет экономический смысл.
, и по той же причине первое отрицательное слагаемое с ростом времени превысит второе. Это приводит к тому, что темп прироста дохода падает и становится с некоторого момента отрицательным, а через некоторое время и сам доход становится равным нулю. После этого модель теряет экономический смысл.
3) случай, когда Y(0) = C(0).
При этом, согласно формуле (20), величина a0 = 0. Следовательно, для модели Харрода-Домара r также будет равно нулю. В формуле (19) первое слагаемое станет равным нулю, а второе слагаемое будет равно Y(0) для всех значений t, т.е. Y(t) = Y(0) = const. Если же увеличивать величину темпа прироста потребления r, используя формулу:
 , (21)
, (21)
где k – увеличивающий коэффициент, то при сохранении условия:Y(0) = C(0) имеем тот же результат.
Таким образом, для получения самоподдерживающегося роста дохода в модели Харрода-Домара необходимо в первоначальный момент иметь превышение дохода над потреблением и чем выше это превышение, тем выше темп прироста дохода.
Исходные данные приведены в таблице 1.
Таблица 1
| B | Y(0) | C(0) 1 случай | C(0) 2 случай | C(0) 3 случай |
АЛГОРИТМ ВЫЧИСЛЕНИЯ ПОКАЗАТЕЛЕЙ и экономический анализ полученных результатов
1. В качестве изучаемой системы берется экономика условного объекта.
2. Используя табличный редактор Excel, рассчитываем по формуле (9) зависимость Y = f1(t) при отсутствии потребления, т.е. C(t) = 0. Значения коэффициента приростной капиталоемкости В и Y(0) приведены в таблице исходных данных. Величину t задаём в пределах от 0 до 20 лет с интервалом Dt = 1 году. Полученные результаты записаны в таблице 2.
Таблица 2
| Y(t) = f1(t) |
| 359,5271 |
| 461,642 |
| 592,76 |
| 761,1189 |
| 977,296 |
| 1254,873 |
| 1611,289 |
| 2068,936 |
| 2656,566 |
| 3411,098 |
| 4379,937 |
| 5623,95 |
| 7221,295 |
| 9272,327 |
| 11905,9 |
| 15287,48 |
| 19629,52 |
| 25204,8 |
| 32363,6 |
| 41555,68 |
Затем, применив "Мастер диаграмм" табличного редактора Excel, строим график зависимости Y = f1(t) (Приложение 1).
По графику Y = f1(t) можно сделать вывод, что в этом случае все ресурсы направляются на инвестиции, в результате чего могут быть определены максимальные технически возможные темпы роста дохода. Непрерывный темп прироста равен  (1/4). Это максимально возможный (технологический) темп прироста дохода в рассматриваемой экономической системе.
(1/4). Это максимально возможный (технологический) темп прироста дохода в рассматриваемой экономической системе.
3. Аналогично производим расчеты значений трех функций Y = f(t) по формуле (13) для трех случаев C(0) при постоянной функции потребления, т.е. C(t) = C(0) = const. Численные значения C(0) для каждого случая берём из таблицы 1.
Полученные результаты записаны в таблице 3.
Таблица 3
| Y(t) = f2(t) | Y(t) = f3(t) | Y(t) = f4(t) |
| 331,1246 | 316,9233 | |
| 396,7698 | 364,33377 | |
| 481,06 | 425,21 | |
| 589,2907 | 503,37664 | |
| 728,2617 | 603,74458 | |
| 906,704 | 732,61958 | |
| 1135,828 | 898,09835 | |
| 1430,03 | 1110,5773 | |
| 1807,792 | 1383,4057 | |
| 2292,849 | 1733,7242 | |
| 2915,674 | 2183,5421 | |
| 3715,397 | 2761,1198 | |
| 4742,261 | 3502,7442 | |
| 6060,781 | 4455,0088 | |
| 7753,795 | 5677,7407 | |
| 9927,667 | 7247,7595 | |
| 12718,97 | 9263,7036 | |
| 16303,08 | 11852,227 | |
| 20905,17 | 15175,957 | |
| 26814,37 | 19443,711 |
Применив "Мастер диаграмм" табличного редактора Excel, строим на одной диаграмме графики зависимостей: Y = f2(t), Y = f3(t), Y = f4(t), С = f5(t), С = f6(t), С = f7(t) (Приложение 2).
По графикам Y = f2(t) и С = f5(t), Y = f3(t) и С = f6(t) можно сделать вывод, что с ростом времени растет доход Y(t), а потребление C(t) = const. В связи с этим непрерывный темп прироста дохода v(t) возрастая, стремится к  при
при  , так как доход растёт, а постоянный объём потребления составляет всё меньшую его долю. Также можно отметить, что графики Y = f2(t), Y = f3(t), С = f5(t), С = f6(t) ниже Y = f1(t) на величину потребления.
, так как доход растёт, а постоянный объём потребления составляет всё меньшую его долю. Также можно отметить, что графики Y = f2(t), Y = f3(t), С = f5(t), С = f6(t) ниже Y = f1(t) на величину потребления.
Необходимо также отметить, что при C(0) = Y(0) непрерывный темп прироста дохода равен нулю и, следовательно, роста дохода вообще не происходит.
4. Для функции потребления, растущей с постоянным темпом:
 (22)
(22)
рассчитываем значения темпов роста r для трех различных значений C(0) по формуле:
 (23)
(23)
Величины B, Y(0) и C(0) выбираются из таблицы исходных данных.
Получаем:
| r1 | r2 | r3 |
| 0,16 | 0,12 |
5. Для каждого полученного значения r рассчитываем значения С = f8(t), С = f9(t), С = f10(t), используя формулу (22), и значения Y = f11(t), Y = f12(t), Y = f13(t), используя формулу (19). Значения t задаём в пределах от 0 до 30 лет с интервалом Dt = 1 году.
Получаем:
Таблица 4
| C = f8(t) | C = f9(t) | C = f10(t) | Y = f11(t) | Y = f12(t) | Y = f13(t) |
| 117,4349 | 168,4614 | 328,8178 | 314,4613 | ||
| 137,9096 | 189,195 | 386,147 | 353,164 | ||
| 161,9541 | 212,4804 | 453,4715 | 396,63 | ||
| 190,1907 | 238,6316 | 532,534 | 445,4457 | ||
| 223,3503 | 268,0015 | 625,381 | 500,2694 | ||
| 262,2913 | 300,986 | 734,4158 | 561,8406 | ||
| 308,0217 | 338,0302 | 862,4607 | 630,9897 | ||
| 361,7251 | 379,6337 | 1012,83 | 708,6495 | ||
| 424,7916 | 426,3575 | 1189,417 | 795,8673 | ||
| 498,8538 | 478,8319 | 1396,791 | 893,8195 | ||
| 585,8286 | 537,7646 | 1640,32 | 1003,827 | ||
| 687,9675 | 603,9506 | 1926,309 | 1127,374 | ||
| 807,9142 | 678,2825 | 2262,16 | 1266,127 | ||
| 948,7736 | 761,7629 | 2656,566 | 1421,957 | ||
| 1114,192 | 855,5176 | 3119,737 | 1596,966 | ||
| 1308,45 | 960,8114 | 3663,661 | 1793,515 | ||
| 1536,578 | 1079,064 | 4302,418 | 2014,253 | ||
| 1804,479 | 1211,871 | 5052,542 | 2262,16 | ||
| 2119,089 | 1361,024 | 5933,45 | 2540,578 | ||
| 2488,551 | 1528,533 | 6967,943 | 2853,262 | ||
| 2922,428 | 1716,659 | 8182,799 | 3204,43 | ||
| 3431,952 | 1927,939 | 9609,466 | 3598,819 | ||
| 4030,311 | 2165,222 | 11284,87 | 4041,748 | ||
| 4732,993 | 2431,709 | 13252,38 | 4539,19 | ||
| 5558,187 | 2730,994 | 15562,92 | 5097,856 | ||
| 6527,254 | 3067,114 | 18276,31 | 5725,28 | ||
| 7665,277 | 3444,603 | 21462,77 | 6429,925 | ||
| 9001,713 | 3868,551 | 25204,8 | 7221,295 | ||
| 10571,16 | 4344,677 | 29599,24 | 8110,064 | ||
| 12414,23 | 4879,403 | 34759,85 | 9108,219 |
С помощью "Мастера диаграмм" табличного редактора Excel, строим на одной диаграмме графики зависимостей: С = f8(t), С = f9(t), С = f10(t), Y = f11(t), Y = f12(t), Y = f13(t) (Приложение 3).
По графикам С = f8(t) и Y = f11(t) [С = f9(t) и Y = f12(t)], когда  = 0,07 [
= 0,07 [ =0,12], причем r < 1/B (0,16 < 0,25 [0,12 < 0,25]), можно сделать вывод, что темп прироста дохода равен темпу прироста потребления. Норма накопления
=0,12], причем r < 1/B (0,16 < 0,25 [0,12 < 0,25]), можно сделать вывод, что темп прироста дохода равен темпу прироста потребления. Норма накопления  в этом случае постоянна во времени и равна
в этом случае постоянна во времени и равна  , а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоёмкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.
, а темп прироста дохода пропорционален норме накопления и обратно пропорционален приростной капиталоёмкости. Именно эта модификация модели экономического роста, в которой постоянна норма накопления, называется моделью Харрода-Домара.
Из графиков С = f10(t) и Y = f13(t) следует,что когда Y(0) = C(0), согласно формуле (20), величина a0 = 0. Следовательно, для модели Харрода-Домара r также будет равно нулю. В формуле (19) первое слагаемое станет равным нулю, а второе слагаемое будет равно Y(0) для всех значений t, т.е. Y(t) = Y(0) = const.
6. Рассчитываем значения темпов роста функции C(t) для трех различных значений C(0) по формуле:
 . (24)
. (24)
Получаем:
| r1 | r2 | r3 |
| 0,2 | 0,15 |
7. Используя формулы (22) и (19), для каждого значения найденного r, рассчитываем зависимости: С = f14(t), С = f15(t), С = f16(t), Y = f17(t), Y = f18(t), Y = f19(t) и строим на одной диаграмме графики этих функций (Приложение 4). Полученные результаты занесены в таблицу 5.
Таблица 5
| C = f14(t) | C = f15(t) | C = f16(t) | Y = f17(t) | Y = f18(t) | Y = f19(t) |
| 122,2494 | 173,4214 | 328,2019 | 313,8159 | ||
| 149,4491 | 200,4999 | 383,1248 | 350,0989 | ||
| 182,7006 | 231,8065 | 445,1267 | 388,4352 | ||
| 223,3503 | 268,0015 | 514,3227 | 428,1195 | ||
| 273,0444 | 309,848 | 590,4384 | 468,0452 | ||
| 333,7951 | 358,2285 | 672,6063 | 506,5583 | ||
| 408,0624 | 414,1633 | 759,0816 | 541,2667 | ||
| 498,8538 | 478,8319 | 846,8537 | 568,7874 | ||
| 609,8457 | 553,598 | 931,1148 | 584,4175 | ||
| 745,5325 | 640,0384 | 1004,54 | 581,7026 | ||
| 911,4089 | 739,9758 | 1056,315 | 551,8746 | ||
| 1114,192 | 855,5176 | 1070,835 | 483,1196 | ||
| 1362,092 | 989,1006 | 1025,956 | 359,6261 | ||
| 1665,149 | 1143,541 | 890,6757 | 160,349 | ||
| 2035,635 | 1322,097 | 622,0389 | -142,592 | ||
| 2488,551 | 1528,533 | 161,0472 | -585,99 | ||
| 3042,238 | 1767,203 | -572,755 | -1218,23 | ||
| 3719,117 | 2043,139 | -1688,42 | -2102,78 | ||
| 4546,598 | 2362,16 | -3332,99 | -3322,66 | ||
| 5558,187 | 2730,994 | -5703,88 | -4986,22 | ||
| 6794,85 | 3157,419 | -9065,04 | -7234,69 | ||
| 8306,661 | 3650,428 | -13768,2 | -10251,7 | ||
| 10154,84 | 4220,416 | -20280,8 | -14275,9 | ||
| 12414,23 | 4879,403 | -29222,1 | -19616,8 | ||
| 15176,32 | 5641,287 | -41410,8 | -26675,4 | ||
| 18552,96 | 6522,133 | -57926,5 | -35971 | ||
| 22680,87 | 7540,517 | -80190,8 | -48175,2 | ||
| 27727,23 | 8717,914 | -110072 | -64156,1 | ||
| 33896,36 | 10079,15 | -150021 | -85034,8 | ||
| 41438,09 | 11652,94 | -203249 | -112258 |
По графикам С = f14(t) и Y = f17(t) [С = f15(t) и Y = f18(t)], когда  (0,25 > 0,2 > 0,16 [0,25 > 0,15 > 0,12]), можно сделать вывод, что темп прироста потребления в этом случае оказывается слишком высоким для экономики. В этом случае коэффициент
(0,25 > 0,2 > 0,16 [0,25 > 0,15 > 0,12]), можно сделать вывод, что темп прироста потребления в этом случае оказывается слишком высоким для экономики. В этом случае коэффициент  в формуле (19) отрицателен, так как
в формуле (19) отрицателен, так как  , и по той же причине первое отрицательное слагаемое с ростом времени превысит второе. Это приводит к тому, что темп прироста дохода падает и становится с некоторого момента отрицательным, а через некоторое время и сам доход становится равным нулю. После этого модель теряет экономический смысл.
, и по той же причине первое отрицательное слагаемое с ростом времени превысит второе. Это приводит к тому, что темп прироста дохода падает и становится с некоторого момента отрицательным, а через некоторое время и сам доход становится равным нулю. После этого модель теряет экономический смысл.
Из графиков С = f16(t) и Y = f19(t) видно, когда Y(0) = C(0), если увеличивать величину темпа прироста потребления r, используя формулу (21), то согласно формуле (20), величина a0 = 0. Следовательно, для модели Харрода-Домара r также будет равно нулю. В формуле (19) первое слагаемое станет равным нулю, а второе слагаемое будет равно Y(0) для всех значений t, т.е. Y(t) = Y(0) = const.
8. Для случая, когда  , т.е. 0,5, рассчитываем по формуле (22) значения С = f20(t), С = f21(t), С = f22(t) и по формуле (19) значения Y = f23(t), Y = f24(t), Y = f25(t), t задаём в пределах от 0 до 30 лет с интервалом Dt = 1 году. В таблице 6 приведены полученные значения:
, т.е. 0,5, рассчитываем по формуле (22) значения С = f20(t), С = f21(t), С = f22(t) и по формуле (19) значения Y = f23(t), Y = f24(t), Y = f25(t), t задаём в пределах от 0 до 30 лет с интервалом Dt = 1 году. В таблице 6 приведены полученные значения:
Таблица №6
| C = f20(t) | C = f21(t) | C = f22(t) | Y = f23(t) | Y = f24(t) | Y = f25(t) |
| 164,87213 | 247,30819 | 461,64196 | 323,057531 | 304,822739 | 257,412278 |
| 271,82818 | 407,74227 | 761,11891 | 354,6859 | 301,207872 | 162,165 |
| 448,16891 | 672,25336 | 1254,8729 | 356,291099 | 238,056647 | -69,35293 |
| 738,90561 | 1108,3584 | 2068,9357 | 294,041485 | 60,5027714 | -546,69788 |
| 1218,2494 | 1827,3741 | 3411,0983 | 108,080928 | -326,52662 | -1456,5063 |
| 2008,5537 | 3012,8305 | 5623,9503 | -305,51185 | -1085,7042 | -3114,2045 |
| 3311,5452 | 4967,3178 | 9272,3265 | -1124,7962 | -2492,8386 | -6049,749 |
| 5459,815 | 8189,7225 | 15287,482 | -2651,9737 | -5012,4284 | -11149,611 |
| 9001,7131 | 13502,57 | 25204,797 | -5396,3735 | -9422,8433 | -19891,665 |
| 14841,316 | 22261,974 | 41555,685 | -10211,968 | -17023,501 | -34733,488 |
| 24469,193 | 36703,79 | 68513,741 | -18524,993 | -29977,458 | -59753,867 |
| 40342,879 | 60514,319 | 112960,06 | -32710,375 | -51877,538 | -101712,16 |
| 66514,163 | 99771,245 | 186239,66 | -56713,834 | -88681,399 | -171797,07 |
| 109663,32 | 164494,97 | 307057,28 | -97079,444 | -150255,33 | -288512,63 |
| 180804,24 | 271206,36 | 506251,88 | -164646,23 | -252922,3 | -482440,07 |
| 298095,8 | 447143,7 | 834668,24 | -277348,5 | -423666,49 | -804093,27 |
| 491476,88 | 737215,33 | 1376135,3 | -464836,83 | -707070 | -1336876,2 |
| 810308,39 | 1215462,6 | 2268863,5 | -776101,88 | -1176755,2 | -2218453,9 |
| 1335972,7 | 3740723,5 | -1292050,7 | -1954257,8 | -3675996,3 | |
| 2202646,6 | 3303969,9 | 6167410,4 | -2146249,6 | -3240152,2 | -6084299,1 |
| 3631550,3 | 5447325,4 | -3559135,1 | -5365381,9 | -10061624 | |
| 5987414,2 | 8981121,3 | -5894431,2 | -8875903,7 | -16627732 | |
| 9871577,1 | -9752184,7 | -14672264 | -27464469 | ||
| -16122176 | -24239744 | -45345421 | |||
| -26636884 | -40027847 | -74844353 | |||
| -43988585 | -66075998 | -123503270 | |||
| -72617095 | -109045210 | -203758311 | |||
| -119843708 | -179919090 | -336115085 | |||
| -197740847 | -296808404 | -554384055 | |||
| -326214681 | -489575148 | -914312361 |
Применив "Мастер диаграмм" табличного редактора Excel, строим на одной диаграмме графики этих зависимостей (Приложение 5).
По графикам С = f20(t) и Y = f23(t), С = f21(t) и Y = f24(t), С = f22(t) и Y = f25(t) видно, когда  (в нашем случае
(в нашем случае  ), то потребление будет занимать всё большую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход. Это также видно из формулы (19) решения модели. Действительно, если
), то потребление будет занимать всё большую часть дохода, что сведёт к нулю сначала инвестиции, а затем и доход. Это также видно из формулы (19) решения модели. Действительно, если  ,то коэффициент
,то коэффициент  отрицателен, а
отрицателен, а  растёт быстрее, чем
растёт быстрее, чем  , следовательно, отрицательное второе слагаемое через некоторое время перевесит первое.
, следовательно, отрицательное второе слагаемое через некоторое время перевесит первое.
ЗАКЛЮЧЕНИЕ
Относительная простота модели позволяет более глубоко изучить взаимосвязь динамики инвестиций и роста выпуска, получить точные формулы траекторий рассматриваемых параметров при сделанных предпосылках.
Исследовав динамики дохода при различной динамике потребления для данной модели, стало ясно, что для получения самоподдерживающегося роста дохода необходимо в первоначальный момент иметь превышение дохода над потреблением и чем выше это превышение, тем выше темп прироста дохода.
Список использованной литературы
1. В.Ф.Пучков методическое пособие «Математические модели макроэкономики» - Гатчина :изд-во ЛОИЭФ, 2005.
2. Венецкий И.Г., Венецкая В.И. Основные математико-статистические понятия и формулы в экономическом анализе.
3. Доугерти К. Введение в эконометрику: Пер. с англ. – М.: ИНФРА-М, 1999. – XIV, 402 с.
4. Елисеева И.И. «Эконометрика»: Учебник – М.: Финансы и статистика, 2001. – 344 с.: ил.
5. Курицкий, Поиск оптимальных решений в EXCEL – М., 2000, 245 с.
6. Политова И.Д. Дисперсионный и корреляционный анализ в эконометрике. Учебное пособие для экономических факультетов. М.: Дело, 1998. – 248 с.
7. Пучков В.Ф. «Эконометрика»: Уч. пособие. Ч. 1. – Гатчина: Изд–во ЛОИЭФ, 2005. – 51 с.
8. Экономико-математические методы и прикладные модели: Уч. пособие / В.В. Федосеев, А.Н. Гармаш, Д.М. Дайитбегов и др.; Под ред. В.В. Федосеева. – М.: ЮНИТИ
ПРИЛОЖЕНИЕ 1

ПРИЛОЖЕНИЕ 2

ПРИЛОЖЕНИЕ 3

ПРИЛОЖЕНИЕ 4

 ПРИЛОЖЕНИЕ 5
ПРИЛОЖЕНИЕ 5