Показатели вариации и их значение в статистике
Понятие вариации и ее значение
Вариация – это различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени.
Например, работники фирмы различаются по доходам, затратам времени на работу, росту, весу и т.д.
Вариация возникает в результате того, что индивидуальные значения признака складываются под совокупным влиянием разнообразных факторов (условий), которые по-разному сочетаются в каждом отдельном случае. Таким образом, величина каждого варианта объективна.
Исследование вариации в статистике имеет большое значение, т.к. помогает познать сущность изучаемого явления. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию (например, о продолжительности жизни людей, доходах и расходах населения, финансовом положении предприятия и т.д.) для принятия научно обоснованных управленческих решений.
Средняя величина дает обобщающую характеристику признака изучаемой совокупности, но она не раскрывает строения совокупности, которое весьма существенно для ее познания. Средняя не показывает, как располагаются около нее варианты осредняемого признака, сосредоточены ли они вблизи средней или значительно отклоняются от нее. Поэтому для характеристики колебания признака используют показатели вариации.
Показатели вариации и их значение в статистике
Для измерения вариации признака в совокупностях используют следующие обобщающие показатели вариации: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
1. Самым распространенным абсолютным показателем является размах вариации (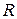 
), определяемый как разность между наибольшим ( 
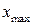) и наименьшим ( 
) значениями вариантов.
. (5.1)
Этот показатель прост для расчета, что и обусловило его широкое распространение. Однако он улавливает только крайние отклонения и не отражает отклонений всех вариант в ряду.
2. Для обобщающей характеристики распределения отклонений рассчитывают среднее линейное отклонение 
, определяемое как средняя арифметическая из отклонений индивидуальных значений от средней, без учета знака этих отклонений:
- невзвешенное среднее линейное отклонение:
, (5.2)
- взвешенное среднее линейное отклонение:
. (5.3)
В этих формулах разности в числителе взяты по модулю, иначе в числителе всегда будет ноль. Поэтому среднее линейное отклонение как меру вариации признака применяют в статистической практике редко, только в тех случаях, когда суммирование показателей без учета знаков имеет экономический смысл. С его помощью, например, анализируется состав работающих, ритмичность производства, оборот внешней торговли.
3. Меру вариации более объективно отражает показатель дисперсии ( 
- средний квадрат отклонений), определяемый как средняя из отклонений, возведенных в квадрат:
- невзвешенная:
, (5.4)
- взвешенная:
. (5.5)
Дисперсия имеет большое значение в экономическом анализе. В математической статистике важную роль для характеристики качества статистических оценок играет их дисперсия.
4. Корень квадратный из дисперсии 
«среднего квадрата отклонений» представляет собой среднее квадратическое отклонение:
. (5.6)
Среднее квадратическое отклонение - это обобщающая характеристика размеров вариации признака в совокупности. Оно показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения; является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому экономически хорошо интерпретируется.
Чем меньше значения дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина.
В статистической практике часто возникает необходимость сравнения вариаций различных признаков (например, сравнение вариаций возраста рабочих и их квалификации, стажа работы и размера заработной платы).
Для осуществления такого рода сравнений используют следующие относительные показатели:
Коэффициент осциляции – отражающий относительную колеблемость крайних значений признака вокруг средней:
. (5.7)
Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:
. (5.8)
Коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средней величины:
. (5.9)
Если 
, то это говорит о большой колеблемости признака в изучаемой совокупности.
5.3 Дисперсия: свойства и методы расчета
Дисперсия обладает рядом свойств, которые позволяют упростить ее расчеты.
1) Если из всех значений вариант отнять какое-то постоянное число 
, то средний квадрат отклонений от этого не изменится:
. (5.10)
2) Если все значения вариант разделить на какое-то постоянное число , то средний квадрат отклонений уменьшится от этого в 
раз, а среднее квадратическое отклонение – в раз.
. (5.11)
3) Если исчислить средний квадрат отклонений от любой величины , которая в той или иной степени отличается от средней арифметической 
, то он всегда будет больше среднего квадрата отклонений , исчисленного от средней арифметической:
. (5.12)
А именно средний квадрат отклонений при этом будет больше на квадрат разности средней и этой условно взятой величиной, т.е. на 
:
. (5.13)
Дисперсия от средней имеет свойство минимальности, т.е. она всегда меньше дисперсий, исчисленных от любых других величин. В этом случае, когда приравнивается к нулю, формула принимает вид:
. (5.14)
Используя второе свойство дисперсии, разделив все варианты на величину интервала, получим следующую формулу вычисления дисперсии в вариационных рядах с равными интервалами по способу моментов:
, (5.15)
где - дисперсия, исчисленная по способу моментов;
– величина интервала,
- новые (преобразованные) значения вариантов ( – условный ноль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой),
- момент второго порядка,
- квадрат момента первого порядка.
Расчет дисперсии по формуле (5.15) менее трудоемок, чем по формулам (5.4) и (5.5).