Перестановки с повторениями

Размещение без повторений

Размещения без повторений — комбинаторные соединения, составленные из n элементов по m. При этом два соединения считаются различными, если они либо отличаются друг от друга хотя бы одним элементом, либо состоят из одних и тех же элементов, но расположенных в разном порядке.

формула для нахождения количества размещений без повторений:


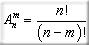
Размещения с повторениями — комбинаторные соединения, составленные из n элементов по m. При этом каждый из n элементов может содержаться сколько угодно раз или вообще отсутствовать.

 

формула для нахождения количества размещений с повторениями:

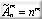
Перестановки.

В комбинаторике перестано́вка — это упорядоченный набор чисел 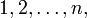обычно трактуемый как биекция на множестве 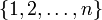, которая числу i ставит соответствиеi-й элемент из набора. Число n при этом называется порядком перестановки. Как синоним слову "перестановка" в этом смысле некоторые авторы используют слово расстановка.

Свойства:

Число всех перестановок порядка 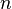равно числу размещений из n по n, то есть факториалу:[1][2][3][4]

Композиция определяет операцию произведения на перестановках одного порядка: Относительно этой операции множество перестановок порядка nобразует группу, которую называют симметрической и обычно обозначают .

Любая группа является подгруппой группы перестановок множества элементов этой группы (теорема Кэли). При этом каждый элемент сопоставляется с перестановкой , задаваемой тождеством где g — произвольный элемент группы G, а — групповая операция.

Сочетания.

В комбинаторике сочетанием из 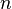по называется набор элементов, выбранных из данного множества, содержащего 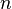различных элементов. Наборы, отличающиеся только порядком следования элементов (но не составом), считаются одинаковыми, этим сочетания отличаются от размещений.

Так, например, наборы (3-хэлементные сочетания, подмножества, ) {2, 1, 3} и {3, 2, 1} 6-тиэлементного множества {1, 2, 3, 4, 5, 6} ( ) являются одинаковыми (однако, как размещения были бы разными) и состоят из одних и тех же элементов {1,2,3}.

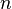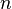В общем случае число, показывающее, сколькими способами можно выбрать элементов из множества, содержащего различных элементов, стоит на пересечении -й диагонали и -й строки треугольника Паскаля.[1]

Сочетания с повторениями.

Сочетанием с повторениями называются наборы, в которых каждый элемент может участвовать несколько раз.

Число сочетаний с повторениями из 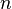по равно биномиальному коэффициенту

При фиксированном 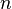производящей функцией чисел сочетаний с повторениями из 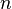по является:

Двумерной производящей функцией чисел сочетаний с повторениями является:

Бином Ньютона.

Бино́м Нью́то́на — формула для разложения на отдельные слагаемые целой неотрицательной степени суммы двух переменных, имеющая вид

,

где — биномиальные коэффициенты, 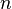— неотрицательное целое число.

В таком виде эта формула была известна ещё индийским и исламским математикам; Ньютон вывел формулу бинома для более общего случая, когда показатель степени — произвольное рациональное число (возможно, отрицательное). В этом случае бином представляет собой бесконечный ряд

Свойства бинома Ньютона

Разложение бинома (a + b)n представляет собой многочлен, расположенный по убывающим степеням a (от n-й до нулевой) и по возрастающим степеням b (от нулевой до n-й); сумма показателей a и b в каждом члене разложения равна показателю степени бинома. Число членов разложения на единицу больше показателя степени бинома.

Коэффициенты членов разложения («биноминальные коэффициенты») возрастают до середины разложения и затем убывают; коэффициенты каждой пары членов, равноотстоящих от начала и конца разложения, равны между собой. Если n четное, то имеется один средний наибольший коэффициент; если n нечетное, то имеется два средних наибольших коэффициента.

При возведении в n-ю степень разности a - b все четные члены разложения имеют знак "минус":

Треугольник Паскаля.

Треугольник Паскаля — бесконечная таблица биномиальных коэффициентов, имеющая треугольную форму. В этом треугольнике на вершине и по бокам стоят единицы. Каждое число равно сумме двух расположенных над ним чисел. Строки треугольника симметричны относительно вертикальной оси. Назван в честь Блеза Паскаля.

Свойства

Числа треугольника симметричны(равны) относительно вертикальной оси.

В строке с номером n:

первое и последнее числа равны 1.

второе и предпоследнее числа равны n.

третье число равно треугольному числу , что также равно сумме номеров предшествующих строк[3].

четвёртое число является тетраэдрическим[3].

m-е число равно биномиальному коэффициенту .

Сумма чисел восходящей диагонали, начинающейся с первого элемента (n-1)-й строки, есть n-е число Фибоначчи:[3]

Если вычесть из центрального числа в строке с чётным номером соседнее число из той же строки, то получится число Каталана.[3]

Сумма чисел n-й строки треугольника Паскаля равна [3].

Все числа в n-й строке, кроме единиц, делятся на число n, если и только если n является простым числом[4] (следствие теоремы Люка).

Простые делители чисел треугольника Паскаля образуют детерминистские фракталы с вращательной симметрией 3-го порядка, которые в полной мере выявляются учётом показателей степеней простых делителей [6] .

Если в строке с нечётным номером сложить все числа с порядковыми номерами вида 3n, 3n+1, 3n+2, то первые две суммы будут равны, а третья на 1 меньше.

Каждое число в треугольнике равно количеству способов добраться до него из вершины, перемещаясь либо вправо-вниз, либо влево-вниз.

Перестановки с повторениями.

Последовательность длины n, составленная из k разных символов, первый из которых повторяется n1 раз, второй — n2 раз, третий — n3 раз,…, k-й — nk раз (где n1+ n2+ … + nk = n) называется перестановкой с повторениями из n элементов.

Например, пусть дан набор из четырех букв aabc. Тогда все перестановки с повторениями из этих букв суть abac, baac, aabc, aacb, abca, baca, acba, acab, bcaa,cbaa, caba, caab.

Число перестановок с повторениями длины n из k разных элементов, взятых соответственно по n1, n2, …, nk раз каждый обозначается P(n1, n2, …, nk) и равно

n! / (n1! n2! … nk!).

В рассмотренном выше примере, букв a в исходном наборе две, а букв b и с — по одной. Следовательно, количество всех перестановок с повторениями из 4 элементов и составом букв 2, 1, 1 равно P(2, 1, 1) = 4! / (2! 1! 1!) = 12, в чем мы и убедились.

Полиномиальная формула.

Формула

(х1+х2+…+хk)n= (1)

 

называется полиномиальной, где суммирование выполняется по всем решениям уравнения n1+n2+ …+ nk = n в целых неотрицательных числах, ni 0, I =1,2,…,k.

 

Для доказательства выполним умножение

 

(х1+х2+…+хk)·(х1+х2+…+хk) … (х1+х2+…+хk) = (х1+х2+…+хk)n.


n

 

Чтобы привести подобные в полученном выражении, необходимо подсчитать количество одночленов вида каждого разбиения n1+n2+ …+ nk = n. Для получения же одночлена необходимо выбрать х1 в качестве множителя в n1 скобках при раскрытии выражения (х1+х2+…+хk)n. Это можно сделать способами. Из оставшихся n – n1 не раскрытых скобок необходимо выбрать х2 в качестве множителя в n2 скобках. Это можно сделать способами и т.д. Тогда количество одночленов при раскрытии выражения

 

(х1+х2+…+хk)·(х1+х2+…+хk) … (х1+х2+…+хk)

 

n

 

будет равно числу … = упорядоченных разбиений.

Рекуррентные соотношения.

!