Вопрос 1. Вероятностные основы моделирования финансового рынка

Далее ⇒

В финансовой экономике принято оперировать понятием актива, относя к нему любую ценность. В зависимости от того, связано или нет владение тем или иным активом с риском, их множество разделяется на рисковые и безрисковые. Риск при этом понимается как та неопределенность в финансовых контрактах с активами, которая может привести к финансовым потерям. Емкими примерами таких активов являются акции и облигации (банковский счет) 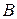. Они образуют основу финансового рынка как пространства, снабженного соответствующей "торговой" инфраструктурой.

Пусть активы 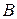(безрисковый) и 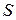(рисковый) полностью определяются в любой момент времени своими ценами. Поэтому естественно считать базисной компонентой финансового рынка эволюцию цен и , которая осуществляется в соответствии с уравнениями

где

, ,

Относительно сразу будем говорить как о постоянной процентной ставке. Величины , определяющие эволюцию цен , уточним несколько позднее.

Ещё одной неотъемлемой компонентой финансового рынка является набор допустимых действий, или стратегий, которые можно производить с активам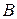и и .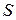

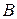Последовательность называется стратегией (портфелем), если для каждого величины и полностью определяются значениями цен . Это означает, что и являются функциями от : и . Их интерпретация – это количество единиц актива и 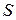соответственно.

С портфелем неразрывно связано понятие капитала портфеля:

где первая компонета показывает, сколько средств лежит на банковском счете, а вторая – сколько вложено в акции.

Если изменение капитала портфеля

происходит только за счет изменения цен банковского счета и акций

то портфель называется самофинансируемым ( ).

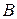Модель эволюции цен и с классом называется -рынком, или финансовым рынком с базовыми активами и .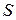

На этом рынке, где активы 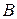и 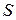играют роль основных ценных бумаг, можно формировать производные ценные бумаги.

Например, форвардный контракт на покупку акции 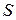в момент времени – это соглашение, регламентирующее одной стороне покупку этой акции, а другой – продажу по цене (цена поставки). Другой контракт – опцион покупателя – это соглашение, дающее право одной стороне на покупку акции по цене (цена исполнения), а другую обязывающее обеспечить продажу акции по цене в момент . В отличие от форвардного опционный контракт предполагает в момент заключения уплату премии.

Общая черта всех производных ценных бумаг – это их "распространенность в будущее" и "оттянутая в будущее выплата" . В первом случае , а во втором . Такие будущие платежи, которые можно отождествлять с производными ценными бумагами, будем называть платежными обязательствами.

Основной проблемой здесь является нахождение цены такого обязательства (или бумаги) в любой момент времени до истечения его срока действия. Ключевым элементом в этой проблеме является хеджирование платежных обязательств.

Портфель называется хеджем для , если при любом поведении рынка. Таких портфелей может быть много и важно выбрать хедж с наименьшим капиталом (минимальный хедж): для любого хеджа при любом развитии рынка (см. рис. 2.1.1):

Рис.2.1.1: Динамика капитала хеджирующих стратегий.

Ясно, что построение минимального хеджа открывает естественный путь решения проблемы цены платёжного обязательства как капитала минимального хеджа, а также управления риском с ним связанным.

Для этого потребуется некоторое уточнение понятия рискового актива в рассматриваемой модели финансового рынка, которое основывается на определенных понятиях из теории вероятностей и стохастического анализа.

Будем исходить из априорного понятия "эксперимент" с вполне определенным знанием его возможных исходов и незнанием того, какой из этих исходов произойдет до проведения эксперимента (случайность эксперимента).

Пример биржевых торгов. Есть знание возможных значений курса рубль/доллар и т. д., но до самих торгов неизвестно, какой же всё-таки будет курс.

Обозначим множество "элементарных" исходов через . Из них образовываются события (неэлементарные исходы), которые формируют множество событий , содержащее невозможное и достоверное события.

Далее, если , то повторение эксперимента раз фиксирует событие раз и соответственно частоту появления . Рассматривают только такие эксперименты, "случайность" которых обладает свойством статистической устойчивости, когда для любого события существует число такое, что при .

Указанное свойство называют статистической устойчивостью эксперимента, а определяемое этим свойством число – вероятностью события . Очевидны свойства вероятности , как функции на :

1) и ;

2) для .

Набор принято называть вероятностным пространством. Часто вместо события рассматривают его индикатор :

если

Индикатор является важным и простым примером случайной величины , как функции от на этом пространстве, когда каждому значению сопоставляется вполне определенное действительное число . В зависимости от того, исчерпывается множество значений случайной величины числовой последовательностью или заполняет целые интервалы, случайную величину называют дискретной или непрерывной соответственно. В этих случаях естественной числовой характеристикой является среднее, или математическое ожидание:

где называется распределением, а неотрицательная функция – плотностью.

Формально обе формулы можно записать в виде

где называют функцией распределения.

Ясно, что в дискретном случае , а в непрерывном

Если – некоторая функция, то можно говорить о случайной величине . Для нее также определено математическое ожидание

соответственно,

если сумма или интеграл в правой части существуют.

В частности, для соответствующее математическое ожидание называется дисперсией :

Примеры распределений:

1) Распределение Бернулли – это распределение случайной величины , принимающей два значения : с вероятностью и с вероятностью ;

2) Биномиальное распределение – это распределение случайной величины, принимающей значения при этом , , ;

3) Пуассоновское распределение (с параметром ) – это распределение случайной величины со значениями и при этом .

4) Нормальное распределение – это распределение случайной величины с плотностью .

Пусть на задана положительная случайная величина c . Для каждого события определим его новую вероятность . Тогда относительно этой новой вероятности случайная величина имеет и новое среднее:

При выводе этой формулы замены вероятности в математическом ожидании была использована линейность, устанавливаемая непосредственно из определения:

для постоянных .

Несколько следующих понятий и фактов обсудим только для дискретных случайных величин и со значениями и соответственно.

Вероятность называется совместным распределением и , при этом и .

Обозначая и , приходим к важному понятию независимости и , означающему, что .

Как следствие, для двух независимых случайных величин и имеем, что .

Условным математическим ожиданием случайной величины при условии, что , называется число .

Случайная величина есть по определению условное математическое ожидание при условии , если совпадает с на множестве .

В частности, для "тривиальных" случайных величин и получаем определение условной вероятности .

Отметим следующие свойства условных математических ожиданий:

1) , что для и соответствует формуле полной вероятности ;

2) для независимых и имеем, что .

3) Ввиду самого определения условное математическое ожидание является функцией от и в этом смысле может интерпретироваться как прогноз на основе информации, доставляемой "наблюдаемой" величиной .

Наконец, для "восстановления" распределения случайной величины , принимающей значения полезно понятие производящей функции , для которой и для независимых случайных величин .

Обратимся снова к примеру биржевых торгов и рассмотрим этот случайный эксперимент от нуля до ( – это "сегодня", – это месяц, квартал, год и т.д.) Ясно, что "элементарный" исход такого эксперимента может быть записан в виде последовательности , где – "элементарный" исход завтрашних торгов и т.д.

Возникает вероятностное пространство таких растянутых до "временного горизонта" торгов.

Если торги рассматривать до каждого момента , то соответствующее пространство имеет элементарные исходы и запас событий .

Таким образом, стремление уловить эволюцию торгов приводит к необходимости рассматривать пространство с выделенным информационным потоком , таким, что , которое принято называть стохастическим базисом (случайного эксперимента торгов).

Вернемся к модели финансового рынка.

Первый актив 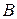считается безрисковым, поэтому разумно предположение о его неслучайности: для всех . Второй актив 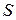– рисковый и разумно отождествить его рисковость со случайностью, предполагая – случайными величинами на описанном выше стохастическом базисе (например, биржевых торгов). При этом, каждая из величин полностью определяется результатами торгов до момента , или набором событий . Будем предполагать, с другой стороны, что случайность механизма торгов полностью исчерпывается ценами акций, что записывается в виде .

Для получения конкретных ответов в предполагаемых финансовых расчетах необходимо конкретизировать механизм случайности цен. Пусть в модели -рынка величины являются случайными, независимыми и принимающими два значения и , где , . Значит, формально представленное выше вероятностное пространство можно отождествить с – пространством последовательностей длины , где на -м месте располагается либо , либо ; – множество всех подмножеств из ; – вероятность, индуцируемая бернуллиевской вероятностью .

Информационный поток, или фильтрация , порождается ценами , или, что эквивалентно, последовательностью :

Последнее просто означает, что любая случайная величина на является функцией от или с учетом их взаимосвязи , Финансовый -рынок, заданный на описанном выше стохастическом базисе, будем называть биномиальным.

Вспоминая проблему хеджирования, сразу отмечаем, что платежное обязательство , исполняемое в последний день торгов, определяется, вообще говоря, событиями всей предыдущей предыстории и, следовательно, является функцией : . Проблема же состоит в возможности оценить на основе доступной лишь к моменту рыночной информации . Значит, необходимо делать оценку, или прогноз, на основе текущей информации , .

Сформулируем те эвристически понятные свойства прогноза, который будем обозначать для .

1) – это функция только от , но не от ненаблюдаемых ещё рыночных цен

2) Прогноз на основе тривиальной информации должен совпадать со средним прогнозируемого платежного обязательства: при , .

3) Прогнозы должны быть согласованы в том смысле, что прогноз совпадает с прогнозом для следующего прогноза . Как следствие, прогноз в среднем совпадает со средним от : .

4) Прогноз по всей доступной информации совпадает с прогнозируемой величиной: .

5) Прогноз для линейной комбинации , где и полностью определяются по информации , равен линейной комбинации прогнозов:

6) Если прогнозируемая величина не зависит от текущей информации , то прогноз на основе такой информации тривиален и равен среднему .

7) Обозначая из свойства 3) получаем, что для всех . Такие стохастические последовательности называются мартингалами.

Значит, если от прогнозов потребовать перечисленные выше естественные свойства, то они образуют мартингал на стохастическом базисе . "Мартингальность" означает, что прогноз для следующего значения прогноза совпадает с его предыдущим значением.

Далее ⇒