Олимпиада по математике для 11-го класса

Министерство образования Республики Беларусь

Белорусский государственный педагогический университет

Им. М. Танка

Выполнили:

Студенты 403 группы математического факультета

Юхневич Александр Олегович

Гриценко Дмитрий Сергеевич

Кононович Владимир Александрович

Минск, 2011

1) Определите а так, чтобы сумма квадратов корней уравнения 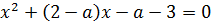была наименьшей.

2) 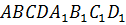- куб с ребром 2 см. Паук находится в центре грани . Какую наименьшую длину может иметь путь паука по поверхности куба в вершину ?

3) Докажите, что доску нельзя замостить фигурами, указанными на рисунке (квадраты доски и фигуры одинаковы)

4) В некоторой области 10 городов соединены железнодорожной сетью. Железнодорожная сеть состоит из участков, любой из которых соединяет только каких – либо два города и не проходит через другие города. Участки между собой не пересекаются, и из каждого города выходит по 3 участка. В области действуют 3 дорожно – эксплутационные фирмы. Они хотят распределить обслуживание железнодорожной сети области между собой так, чтобы каждый участок обслуживала только одна фирма, но никакие два участка, выходящие из одного города, не обслуживались бы одной и той же фирмой. Приведите пример, показывающий, что такое распределение не всегда возможно.

5) У одиннадцатиклассника Васи в кармане лежит 100 одинаковых по форме карточек, на которых написаны натуральные числа от 1 до 100 (каждое число – ровно на одной карточке). Вася вынимает наугад часть карточек и смотрит, какие числа на них написаны. Какое наименшее количество карточек должен вынуть Вася, чтобы среди записанных на них чисел заведомо нашлось пять, сумма которых делится на 3?

№1	№2	№3	№4	№5	Итого

1) Найдём сумму квадратов корней уравнения:

. Значение данного выражения будет наименьшим при . При этом значение a дискриминант левой части уравнения положителен, поэтому корни существуют. Ответ: .

Так как О центр квадрата ,

Рассмотрим (Угол ) :

Ответ:

Используем шахматную раскраску доски. Всего получилось по 50 белых и черных квадратов. Одна фигурка, как бы не располагалась на доске, покрывает три квадрата одного цвета и один другого. Пусть 50 черных квадратов мы покрываем n раз по 3, и mпо одному. То есть, . Но при этом одновременно будут покрываться и белые квадраты, и для них соответственно придется написать . Если теперь решить систему

, то получим, что n=12,5 и m=12,5. Так что целыми фигурками замостить доску не удается.

Рассмотрим следующую схему соединения городов участками железной дороги (города обозначены точками, а участки рельсами). Предположим, что участки можно распределить между тремя фирмами так, как требуется в условии задачи. Обозначим фирмы 1, 2, 3. Без ограничения общности участки, выходящие из города А, расположены так, показано на рисунке: участок АВ обслуживает фирма 1, участок АС – фирма 2 и участок АD – фирма 3. Так как участки ВА и СА обслуживаются фирмами, соответственно, 1 и 2, то участок ВС должна обслуживать фирма 3 (поскольку, в противном случае, участки, выходящие из города В или С, обслуживала бы одна и та же фирма). Поэтому участок ВЕ должна обслуживать фирма 2, а участок СD – фирма 1. Но тогда участок DE не может (с соблюдением условий задачи) обслуживать ни одна фирма. В самом деле, так как участки DA и DC обслуживают, соответственно фирмы 3 и 1, то участок DE должна обслуживать фирма 2, то есть участки EB и ED, выходящие из города Е, обслуживает одна и та же фирма 2. Требуемый пример построен.

Докажем, что если Вася вытянет 36 карточек, то среди чисел, записанных на них, найдутся 5 чисел, сумма которых кратна 3. Предположим, что это не так, то есть что среди натуральных чисел от 1 до 100 найдутся такие 36 чисел, сумма никаких 5-и из которых не делится на 3. Тогда среди этих 36 чисел не может быть двух чисел кратных 3. В самом деле, пусть имеются 2 числа, каждое из которых кратно 3 (обозначим их a и b). Рассмотрим оставшиеся 34 числа. Так как целые числа при делении на 3 дают 3 различных остатка (0,1, 2), то среди этих 34 чисел заведомо найдутся 3 числа, имеющих один и тот же остаток при делении на 3. Сумма этих трёх чисел и чисел a и b (т. е. сумма 5-и чисел из 36) кратна 3, чего по предположению быть не может. Следовательно, из этих 36 чисел не менее 35-и при делении на 3 дают остаток 1 или 2. Допустим, что среди них имеются как числа, дающие при делении на 3 остаток 1, так и числа, дающие при делении на 3 остаток 2. Тогда выберем из этих 35 чисел 2 числа, имеющих разные остатки; сумма выбранных 2-х чисел кратна 3 (действительно, сумма чисел 3k+1 и 3m+2, где k и m целые, равна 3(k+m+0), т. е. кратна 3). Среди оставшихся 33-х чисел заведомо найдутся 3, имеющих при делении на 3 один и тот же остаток. Поэтому сумма этих 3-х чисел и уже выбранных 2-х кратна 3, что по предположению невозможно. Следовательно, все 35 чисел при делении на 3 должны давать либо только остаток 1, либо только остаток 2. Но это невозможно, поскольку среди натуральных чисел от 1 до 100 имеются ровно 34 числа с остатком 1 и ровно 33 числа с остатком 2 при делении на 3. Стало быть, какие бы 36 карточек Вася не вытянул, среди записанных на них чисел найдутся 5 с суммой, кратной 3. Остаётся доказать, что среди натуральных чисел от 1 до 100 можно выбрать таких 35 чисел, сумма каждых 5-и из которых не делится на 3. В самом деле выберем эти 35 чисел так: все 34 числа дающие при делении на 3 остаток 1 и число 3. Сумма никаких 5-и из них не делится на 3, поэтому такая сумма - это либо сумма 5-и чисел имеющих остаток 1 при делении на 3 (тогда она при делении на 3 даёт остаток 2), либо сумма четырёх чисел имеющих при делении на 3 остаток 1, и числа 3 (тогда она при делении на 3 даёт остаток 1).

ЛИТЕРАТУРА:

Задача 1 – А. В. Фарков “Математические олимпиады в школе 5-11 классы”, стр. 53, Вариант 1, №1

Задача 2 – А. В. Фарков “Математические олимпиады в школе 5-11 классы”, стр. 53, Вариант 1, №3

Задача 3 – Т.П. Бахтина “Раз задачка, два задачка... ” Пособие для учителей, стр. 144, № 239

Задача 4 – Задачи районного тура Минской городской математической олимпиады школьников (1991-2001 гг.)/ Е.А. Барабанов, И.И. Воронович, В.И. Каскевич, С.А. Мазаник, стр. 31, № 168

Задача 5 – Задачи районного тура Минской городской математической олимпиады школьников (1991-2001 гг.)/ Е.А. Барабанов, И.И. Воронович, В.И. Каскевич, С.А. Мазаник, стр. 37, № 193