Если ряд (2) сходится, то ряд (1) также сходится,
2) если ряд (1) расходится, то ряд (2) также расходится.
Замечание. Признаки сравнения применимы и в том случае, когда условие 
выполняется не при всех n, а лишь начиная с некоторого n = N.
Пример 1.Исследовать на сходимость ряд 
.
Решение.Оценим общий член данного ряда: 
. Ряд с общим членом 
сходится (геометрический ряд). По теореме 1(п.1) данный ряд также сходится.●
Пример 2. Исследовать на сходимость ряд 
.
Решение.Рассмотрим вспомогательный ряд
,
который расходится (см. пример 3, §4). Так как
,
то по теореме 1(п.2) данный ряд также расходится. ●
Теорема 2 (второй признак сравнения рядов). Пусть даны два знакоположительных ряда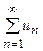 
(1) и 
(2). Если существует конечный, отличный от нуля, предел отношения общих членов этих рядов: 
, то оба ряда сходятся или расходятся одновременно.
Смысл этого признака состоит в том, что если общий член ряда (1) и общий член ряда (2) являются бесконечномалыми одного и того же порядка (при 
), то сходимость одного из этих рядов влечет сходимость другого (а значит, и, наоборот, расходимость одного влечет расходимость другого).
При исследовании сходимости рядов с помощью признаков сравнения необходимо иметь для сравнения ряды, относительно которых известно, сходятся они или расходятся. В качестве таких рядов часто используют геометрический ряд, а также
– обобщенный гармонический ряд,
который сходится при 
и расходится при 
. Это будет доказано ниже.
При 
получается
– гармонический ряд.
Пример 1. Исследуем сходимость ряда 
.
Решение. Рассмотрим вспомогательный ряд 
, который сходится.
Вычисляем 
. Значит, по теореме 2 данный ряд сходится. ●
Пример 2. Исследуем сходимость ряда 
Решение. Рассмотрим вспомогательный ряд 
, который расходится.
Вычисляем 
. Значит, по теореме 2 данный ряд расходится. ●
Признак Даламбера
Теорема. Если для знакоположительного ряда 
существует предел отношения последующего члена к предыдущему при неограниченном возрастании п, т.е.
,
то при 
ряд сходится, а при 
ряд расходится.
Пример 1. Выясним, сходится ли ряд 
.
Решение. Имеем 
.
Вычисляем 
.
На основании признака Даламбера данный ряд сходится. ●
Пример 2. Исследуем сходимость ряда 
.
Решение. Имеем 
.
Вычисляем 
На основании признака Даламбера данный ряд расходится. ●
Замечание. В тех случаях, когда 
или не существует, признак Даламбера не дает ответа на вопрос о том, сходится или расходится ряд.
При этом ряд может оказаться как сходящимся, так и расходящимся. В этом случае применяются другие признаки.
Пример.Исследуем сходимость ряда 
.
Решение.Имеем 
.
Вычисляем 
.
Признак Даламбера не дает ответа на вопрос о сходимости данного ряда. По первому признаку сравнения: 
при всех значениях n, а ряд с общим членом 
сходится. Следовательно, данный ряд сходится. ●
Радикальный признак Коши
Теорема. Если для знакоположительного ряда существует предел 
, то при ряд сходится, а при ряд расходится.
Пример. Выясним, сходится ли ряд 
.
Решение.Вычисляем
.
На основании радикального признака Коши ряд сходится. ●
Замечание. Если 
не существует или равен 1, то признак Коши, как и признак Даламбера, не дает ответа на вопрос о сходимости ряда.
Интегральный признак Коши
Теорема. Пусть дан знакоположительный ряд (1). Если существует положительная, непрерывная, монотонно убывающая на 
функция 
, такая, что 
, 
, … 
, … то
1) ряд (1) сходится,если интеграл 
сходится;
2) ряд (1) расходится,если интеграл 
расходится.
Пример 1. Исследуем сходимость ряда 
.
Решение. 
– непрерывная при 
функция, убывает с возрастанием х.
Несобственный интеграл сходится, следовательно, данный ряд сходится. ●
Пример 2. Исследуем на сходимость ряд 
, где 
.
Решение. Рассмотрим 
. Эта функция удовлетворяет всем условиям теоремы, рассмотренной выше. Вычислим
а) пусть 
, тогда 
при 
и интеграл
.
На основании интегрального признака Коши ряд расходится.
б) пусть , тогда
.
На основании интегрального признака Коши ряд расходится.
в) пусть , тогда 
при и интеграл
.
На основании интегрального признака Коши ряд сходится. ●
Знакочередующиеся ряды
Знакопеременным рядом называется ряд, членами которого являются действительные числа произвольного знака. Ряд, в котором за каждым положительным членом следует отрицательный и за каждым отрицательным членом следует положительный, называют знакочередующимся.
Обозначим 
– абсолютные величины членов ряда. Будем считать, что первый член ряда положителен. Тогда знакочередующийся ряд можно записать в виде:
(1)
Для знакочередующихся рядов имеет место достаточный признак сходимости Лейбница.
Теорема (признак Лейбница). Если члены знакочередующегося ряда удовлетворяют условиям: 1) 
, 2_ 
, то ряд сходится и его сумма 
.
Или: если в знакочередующемся ряде абсолютные величины членов убывают, и общий член ряда стремится к нулю, то ряд сходится, и его сумма не превосходит членов ряда.
Пример.Исследуем, сходится или расходится ряд
Решение. Этот ряд удовлетворяет условиям признака Лейбница:
1) 
,
2) 
.
Следовательно, ряд сходится.●