Тема 8. Неопределенный интеграл. Методы вычисления
Первообразная функция. Неопределенный интеграл. Свойства неопределенного интеграла. Таблица основных интегралов. Основные методы интегрирования. Интегрирование рациональных функций. Интегрирование выражений, содержащих тригонометрические функции. Интегрирование некоторых иррациональных функций. Использование таблиц интегралов.
Методические рекомендации
В предыдущих разделах мы изучали производную функции и ее приложения к решению практических задач.
В этом разделе рассматривается второе основное понятие математического анализа понятие интеграла. Интегрирование действие, обратное нахождению производной. Важно усвоить основные формулы интегрирования и методы интегрирования, т.к. понятие интеграла пронизывает не только всю современную математику, но и физику, химию и многие общетехнические и специальные дисциплины.
Литература: /2, глава 6 §1-6/, или /4, глава 7 §1-6/,или /5(ч.1), глава 9/.
Вопросы для подготовки к экзамену:
1. Первообразная функция. Неопределенный интеграл и его свойства. Таблица основных интегралов.
2. Основные методы интегрирования: непосредственное интегрирование, замена переменной, интегрирование по частям.
3. Простейшие рациональные дроби и их интегрирование.
4. Правильные и неправильные рациональные дроби. Разложение правильной рациональной дроби на простейшие. Интегрирование дробно-рациональных функций.
5. Интегрирование некоторых видов тригонометрических функций. Универсальная тригонометрическая подстановка. Интегралы вида: 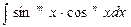
6. Интегрирование некоторых видов иррациональных выражений. Тригонометрические подстановки.
Тема 9. Определенный интеграл. Приложения
Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла. Формула Ньютона-Лейбница. Вычисление определенного интеграла: интегрирование по частям и подстановкой. Приложение интегралов к вычислению площадей плоских фигур, длин дуг кривых, объемов тел и площадей поверхностей вращения. Приближенное вычисление определенного интеграла: формулы прямоугольников, трапеций и Симпсона. Несобственные интегралы.
Методические рекомендации
К понятию определенного интеграла приводит задача вычисления площади криволинейной трапеции. Важное значение имеет формула Ньютона-Лейбница. Эта формула устанавливает связь между двумя основными понятиями интегрального исчисления: неопределенным и определенным интегралами. Она позволяет вычислять определенные интегралы путем нахождения первообразных.
Геометрические приложения определенного интеграла многочисленны. Это вычисление: площадей плоских фигур, объема тел вращения, длин дуг.
Многие задачи механики, например, вычисление давления жидкости на пластину; вычисление работы переменной силы на прямолинейном отрезке пути; вычисление работы по выкачиванию жидкости из резервуара можно решить, используя методы интегрирования.
Литература: /2, глава 6 §7-11/, или /4, глава 8 §1-11/, или /5(ч.1), глава 10/.
Вопросы для подготовки к экзамену:
1. Геометрический смысл определенного интеграла.
2. Основные свойства определенного интеграла.
3. Формула Ньютона-Лейбница.
4. Замена переменной в определенном интеграле.
5.Формула интегрирования по частям для определенного интеграл.
6. Несобственные интегралы (случай бесконечных пределов интегрирования).
7. Несобственные интегралы (интегралы от разрывных функций).
8. Вычисление площадей плоских фигур в декартовых координатах.
9. Вычисление площади под кривой, заданной параметрически.
10. Вычисление площади криволинейного сектора в полярных координатах.
11. Вычисление длин дуг плоских кривых.
12. Вычисление объемов тел вращения.
13. Вычисление площади поверхности тел вращения