Принцип возможных перемещений

Далее ⇒

Элементы аналитической механики

В своих попытках познать окружающий мир человеческой природе свойственно стремление свести систему знаний в данной области к наименьшему числу исходных положений. Это прежде всего относится к научным областям. В механике такое стремление привело к созданию фундаментальных принципов, из которых вытекают основные дифференциальные уравнения движения для различных механических систем. Настоящий раздел учебника призван познакомить читателя с частью этих принципов.

Начнем изучение элементов аналитической механики с рассмотрения вопроса о классификации связях, встречающихся не только в статике, но и в динамике.

Классификация связей

Связь – любого вида ограничения, накладываемые на положения и скорости точек механической системы.

Связи классифицируют:

· По изменению во времени:

- нестационарныесвязи, т.е. меняющиеся со временем. Движущаяся в пространстве опора – пример нестационарной связи.

- стационарныесвязи, т.е. не меняющиеся со временем[7]. К стационарным связям относятся все связи, рассмотренные в разделе «Статика».

· По типу накладываемых кинематических ограничений:

- геометрическиесвязи накладывают ограничения на положения точек системы;

- кинематические, или дифференциальныесвязи накладывают ограничения на скорости точек системы. По возможности сведения одного типа связи к другой:

- интегрируемая, или голономная (простая) связь, если кинематическую (дифференциальную) связь можно представить как геометрическую. В таких связях зависимости между скоростями удается свести к зависимости между координатами. Катящейся без проскальзывания цилиндр – пример интегрируемой дифференциальной связи: скорость оси цилиндра связана с его угловой скоростью по известной формуле 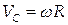, или 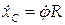, а после интегрирования приводится к геометрической связи между смещением оси и углом поворота цилиндра в виде .

- неинтегрируемая, или неголономнаясвязь – если кинематическую (дифференциальную) связь нельзя представить как геометрическую. Пример – качение шара без проскальзывания при его непрямолинейном движении.

· По возможности «освобождения» от связи:

- удерживающиесвязи, при которых налагаемые ими ограничения сохраняются всегда, например, маятник, подвешенный на жестком стержне;

- неудерживающие связи - ограничения могут нарушаться при определенном типе движения системы, например, маятник, подвешенный на сминаемой нити.

Принцип возможных перемещений

Введем несколько определений.

· Возможное (или виртуальное) перемещение (обозначается ) является элементарным (бесконечно малым) и таково, что не нарушает наложенные на систему связи.

Пример: точка, находясь на поверхности, в качестве возможных имеет множество элементарных перемещений в любом направлении вдоль опорной поверхности, не отрываясь от нее. Движение точки, приводящее к ее отрыву от поверхности, нарушает связь и, в соответствии с определением, не является возможным перемещением.

Для стационарных систем обычное действительное (реальное) элементарное перемещение входит во множество возможных перемещений.

· Число степеней свободы механической системы – это число независимых между собой ее возможных перемещений.

Так, при перемещение точки на плоскости любое ее возможное перемещение выражается через две свои ортогональные (а значит и независимые) составляющие.

У механической системы с геометрическими связями число независимых координат, определяющих положение системы, совпадает с числом ее степеней свободы.

Таким образом, точка на плоскости имеет две степени свободы. Свободная материальная точка – три степени свободы. У свободного тела – шесть (добавляются повороты по углам Эйлера) и т.д.

· Возможная работа – это элементарная работа силы на возможном перемещении.

(3.80)

Будем помечать возможную работу активной силы индексом a ( ) , а возможную работу силы реакции связи индексом r ( ).

· Идеальные связи – связи, для которых сумма элементарных работ их реакций на любом возможном перемещении системы рана нулю:

(3.81)

Принцип возможных перемещений

Если система находится в равновесии, то для любой ее точки выполняется равенство , где - равнодействующие действующих на точку активных сил и сил реакций. Тогда и сумма работ этих сил при любом перемещении также равна нулю . Просуммировав для всех точек, получим: . Второе слагаемое для идеальных связей равно нулю, откуда формулируется принцип возможных перемещений:

(3.82)

В условиях равновесия механической системы с идеальными связями сумма элементарных работ всех действующих на нее активных сил при любом возможном перемещении системы равна нулю.

Ценность принципа возможных перемещений заключается в формулировке условий равновесия механической системы (3.81), в которых не фигурируют неизвестные реакции связей.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Какое перемещение точки называется возможным?

2. Что называется возможной работой силы?

3. Сформулируйте и запишите принцип возможных перемещений.

Принцип Даламбера

Перепишем уравнение динамики к-й точки механической системы (3.27), перенеся левую часть в правую. Введем в рассмотрение величину

(3.83)

Векторная величина, имеющая размерность силы, равная произведению массы точки на ее ускорение и направленная противоположно этому ускорению, называетсясилой инерцииточки

Перепишем уравнение динамики к-й точки механической системы (3.27), перенеся левую часть в правую. Воспользуемся определением (3.83):

(3.84)

Силы в уравнении (3.83) образуют уравновешенную систему сил.

Распространяя этот вывод ко всем точкам механической системы, придем к формулировке принципаДаламбера, названного в честь французского математика и механика Жана Лерона Даламбера (1717–1783 г.г.), рис.3.13:

Рис.3.13

Если ко всем силам, действующим в данной механической системе, добавить все силы инерции, полученная система сил будет уравновешенной и к ней можно применять все уравнения статики.

Фактически это означает, что от динамической системы путем добавления сил инерции (сил Даламбера) переходят к псевдостатической (почти статической) системе.

Используя принцип Даламбера, можно получить оценку главного вектора сил инерции и главного момента сил инерции относительно центра в виде:

(3.85)

Напишем уравнения равновесия для полученной системы в векторной форме:

(3.86)

Динамические реакции, действующие на ось вращающегося тела

Рассмотрим твердое тело, вращающееся равномерно с угловой скоростью ω вокруг оси, закрепленной в подшипниках АиВ(рис. 3.14). Свяжем с телом вращающиеся вместе с ним оси Ахуz;преимущество таких осей в том, что по отношению к ним координаты центра масс и моменты инерции тела будут величинами постоянными. Пусть на тело действуют заданные силы . Обозначим проекции главного вектора всех этих сил на оси Ахуz через ( и т.д.), а их главные моменты относительно тех же осей - через ( и т.д.); при этом, так как ω=const, то =0.

Рис.3.14

Для определения динамических реакций Х_А, У_А, Z_А, Х_B, Y_B подшипников, т.е. реакций, возникающих при вращении тела, присоединим ко всем действующим на тело заданным силам и реакциям связей силы инерции всех частиц тела, приведя их к центру А. Тогда силы инерции будут представлены одной силой, равной и приложенной в точке А, и парой сил с моментом, равным . Проекции этого момента на оси к и у будут: , ; здесь опять , так как ω=const.

Теперь, составляя согласно принципу Даламбера уравнения (3.86) в проекциях на оси Ахуz и полагая АВ=b, получим

(3.87)

Последнее уравнение удовлетворяется тождественно, так как .

Главный вектор сил инерции , где т — масса тела (3.85). При ω=const центр масс С имеет только нормальное ускорение , где - расстояние точки С от оси вращения. Следовательно, направление вектора совпадаете с направлением ОС. Вычисляя проекции на координатные оси и учитывая, что ,где - координаты центра масс, найдем:

Чтобы определить и , рассмотрим какую-нибудь частицу тела с массой m_k, отстоящую от оси на расстоянии h_k. Для нее при ω=const сила инерции тоже имеет только центробежную составляющую , проекции которой, как и вектора R", равны:

Тогда

Составляя такие выражения для всех точек тела, складывая их и вынося общий множитель за скобки, придем к равенствам:

(3.88)

где величины , , поскольку они входят в выражения моментов центробежных сил инерции, носят названия центробежных моментов инерции. Подставляя все найденные значения в равенства (3.87), получим

(3.89)

Уравнения (94) и определяют динамическое реакции, действующие на ось[8] равномерно вращающегося твердого тела.

ВОПРОСЫ ДЛЯ САМОКОНТРОЛЯ

1. Чему равна и как направлена сила инерции точки?

2. Чему равна и как направлена сила инерции точки, равномерно движущейся по окружности?

3. Сформулируйте принцип Даламбера.

Общее уравнение динамики

Принцип возможных перемещений дает общий метод решения задач статики. С другой стороны, принцип Даламбера позволяет использовать методы статики для решения задач динамики. Следовательно, применяя эти два принципа одновременно, можно получить общий метод решения задач динамики.

Итак, переведя динамическую систему сил в псевдостатическую, а затем используя принцип возможных перемещений, получим формулировку принципа Даламбера – Лагранжа в виде:

(3.90)

Далее ⇒