Информация, данные, сигналы
Термин "сигнал" (signal, от лат. signum – знак) используется в широком смысловом диапазоне. Под ним понимают:
· техническое средство для передачи, обращения и использования информации - электрический, магнитный, оптический сигнал;
· физический процесс, представляющий собой материальное воплощение информационного сообщения - изменение какого-либо параметра носителя информации (напряжения, частоты, мощности электромагнитных колебаний, интенсивности светового потока и т.п.) во времени, в пространстве или в зависимости от изменения значений каких-либо других аргументов;
· смысловое содержание определенного физического состояния или процесса, например, сигналы светофора, звуковые предупреждающие сигналы и т.п.
Эти понятия объединяет конечное назначение сигналов. Это определенные сведения, сообщения, информация о каких-либо процессах, состояниях или физических величинах объектов материального мира, выраженные в форме, удобной для передачи, обработки, хранения и использования этих сведений.
Термин “сигнал” часто отождествляется с понятиями “данные” (data) и “информация” (information). Действительно, эти понятия взаимосвязаны и не существуют одно без другого, но относятся к разным категориям.
В настоящее время мировая наука склоняется к точке зрения, что информация, наряду с материей и энергией, принадлежит к фундаментальным философским категориям естествознания и относится к одному из свойств объективного мира. Что касается “данных” (от лат. datum – факт), то это совокупность фактов, результатов наблюдений, измерений о каких-либо объектах, явлениях или процессах материального мира, представленных в формализованном виде, количественном или качественном [2]. Это не информация, а только атрибут информации - сырье для получения информации путем соответствующей обработки и интерпретации (истолкования). Термин "сигнал" является общепринятым для характеристики формы представления данных, при которой данные рассматриваются как результат некоторых измерений объекта исследований в виде последовательности значений скалярных величин (аналоговых, числовых, графических и пр.) в зависимости от изменения каких-либо переменных значений (времени, энергии, температуры, пространственных координат, и пр.). С учетом этого, в дальнейшем термином “сигнал” будем обозначать упорядоченное отображение в изменении физического состояния какого-либо объекта – материального носителя сигнала, определенных данных о характере изменения в пространстве, во времени или по любой другой переменной физических величин, физических свойств или физического состояния объекта исследований. При этом материальная форма носителей сигналов (механическая, электрическая, магнитная, акустическая, оптическая и любая другая), также как и форма отображения в каких-либо физических параметрах или процессах носителей, значения не имеет. Информативным параметром сигнала может являться любой параметр носителя сигнала, функционально связанный со значениями информационных данных.
Сигнал, в самом общем смысле, это зависимость одной величины от другой, и с математической точки зрения представляет собой функцию. Наиболее распространенное представление сигналов - в электрической форме в виде зависимости напряжения от времени U(t).
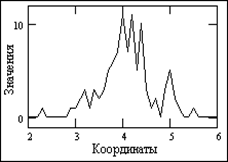
Информация – это мера неопределенности субъективных представлений о физическом объекте, системе или среде.
| Рис. 2.1. Сигнал |
Сигнал - это функция, несущая сообщение (данные) о физических свойствах, состоянии или поведении какой-либо физической системы, объекта или среды
Данные – это элемент (порция) информации о физическом объекте, системе или среде, обычно представленные в хорошо формализованном виде.
С точки зрения теории систем передачи данных важным является следующее соображение: сигнал выступает средством материализации данных, благодаря сигналам данные могут передаваться и обрабатываться с целью извлечения информации [2]. В процессе передачи сигналы могут менять свои свойства (усиливаться, изменять спектр и т.д.) тогда как данные (следовательно, информация), составляющие сообщение, которое переносит сигнал, остаются неизменными на всем пути от источника до приемника.
2.2 Шумы и помехи [2], [5]
При приеме сигналов, несущих целевую для данного вида измерений информацию, вместе с основным сигналом одновременно регистрируются и мешающие сигналы - шумы и помехи самой различной природы (рис. 2.2).
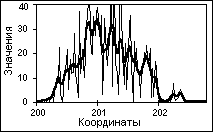
Рис. 2.2. Сигнал с помехами.
Типы помех разделяют по источникам их возникновения, по энергетическому спектру, по характеру воздействия на сигнал, по вероятностным характеристикам и другим признакам.
Источники помех бывают внутренние и внешние. Внутренние шумы могут быть присущи физической природе источников сигналов, как, например, тепловые шумы электронных потоков в электрических цепях или дробовые эффекты в электронных приборах, или возникают в измерительных устройствах и системах передачи и обработки сигналов от влияния различных дестабилизирующих факторов - температуры, повышенной влажности, нестабильности источников питания, влияния механических вибраций на гальванические соединения, и т.п. [5]
Внешние источники шумов бывают искусственного и естественного происхождения. К искусственным источникам помех относятся индустриальные помехи - двигатели, переключатели, генераторы сигналов различной формы и т.д. Естественными источниками помех являются молнии, флюктуации магнитных полей, всплески солнечной энергии, и т.д.
Электрические и магнитные поля различных источников помех вследствие наличия индуктивных, емкостных и резистивных связей создают на различных участках и цепях сигнальных систем паразитные разности потенциалов и токи, накладывающиеся на полезные сигналы [5].
Помехи подразделяются на флуктуационные, импульсные и периодические. Флуктуационные или шумовые помехи представляют хаотический и беспорядочный во времени процесс в виде нерегулярных случайных всплесков различной амплитуды. Как правило, флуктуационные помехи распределены по нормальному закону с нулевым средним и оказывают существенное влияние только на сигналы низкого уровня.
Импульсные помехи во многом похожи на шумовые помехи и проявляются как в виде отдельных импульсов, так и в виде последовательности импульсов, форма и параметры которых имеют случайный характер. Причинами импульсных помех являются резкие броски тока и напряжения в промышленных установках, транспортных средствах, а также природные электрические явления. Распределение импульсных помех симметричное с произвольной плотностью распределения.
Периодические помехи вызываются периодическими низкочастотными или высокочастотными полями линий электропередач, силовых электроустановок и др. Если основная мощность помех сосредоточена на отдельных участках диапазона частот, например, на частоте напряжения промышленной сети или кратна этой частоте, то такие помехи называют сосредоточенными.
В зависимости от характера воздействия на сигнал помехи подразделяются на аддитивные и мультипликативные. Аддитивные (налагающиеся) помехи суммируются с сигналом, не зависят от его значений и формы и не изменяют информативной составляющей самого сигнала. Мультипликативные или деформирующие помехи могут изменять форму информационной части сигнала, иметь зависимость от его значений и от определенных особенностей в сигнале и т.п. При известном характере мультипликативных помех возможна коррекция их влияния на сигнал.
Следует заметить, что деление сигналов на полезные и мешающие (шумовые) является достаточно условным. Источниками мешающих сигналов также являются определенные физические процессы, явления или объекты. Совершенствование методов обработки сигналов с помехами привело к появлению многих перспективных направлений в теории сигналов и систем: Наличие априорной информации о свойствах шумовых процессов позволяет эффективно снизить уровень шумов (задачи оптимального приема и обработки сигналов). В отсутствии априорных данных создаются методы, устойчивые к отклонениям в характеристиках рабочих процессов (робастные методы), среди которых наиболее перспективными являются самонастраивающиеся (адаптивные) методы [5].
2.3 Размерность сигналов [2],[5]
Простейшими сигналами являются одномерные сигналы, как, например, сейсмические импульсы s(t), измерения каких-либо параметров электромагнитных полей и т.п. Значения одномерных сигналов зависят только от одной независимой переменной (рис. 2.1 и 2.2.)

Рис. 2.3. Двумерный сигнал.
В общем случае сигналы являются многомерными функциями пространственных, временных и прочих независимых переменных - Все большее применение находят также многомерные сигналы, образованные некоторым множеством одномерных сигналов, как, например, комплексные измерения нескольких физических параметров одновременно.Многомерные сигналы могут иметь различное представление по своим аргументам.
Многомерный сигнал может рассматриваться, как упорядоченная совокупность одномерных сигналов. С учетом этого при анализе и обработке сигналов многие принципы и практические методы обработки одномерных сигналов, математический аппарат которых развит достаточно глубоко, распространяются и на многомерные сигналы. Физическая природа сигналов для математического аппарата их обработки значения не имеет.
2.4 Математическое описание сигналов [2],[3],[5],[6]
Сигналы могут быть объектами теоретических исследований и практического анализа только в том случае, если указан способ их математического описания - математическая модель сигнала. Как правило, описание сигнала задается функциональной зависимостью определенного информационного параметра сигнала от независимой переменной (аргумента) – s(х), y(t) и т.п.[1] Такая форма описания и графического представления сигналов называется динамической (сигнал в реальной динамике его поведения по аргументам). Функции математического описания сигналов могут быть как вещественными, так и комплексными. Выбор математического аппарата описания определяется простотой и удобством его использования при анализе и обработке сигналов.
2.5 Спектры сигналов [2],[3],[5],[6]
Принцип моделирования реального сигнала аналитической функцией некоторого (возможно бесконечного) числа переменных f(t1, t2,…tn) позволяет при его анализе и обработке широко использовать математическое описание по аргументам, обратным аргументам динамического представления [2],[6]. Так, например, для времени обратным аргументом является частота. Возможность такого описания определяется тем, что любой сколь угодно сложный по своей форме сигнал, кусочно-непрерывный и дифференцируемый, не имеющий разрывов второго рода (бесконечных значений на интервале своего задания), можно представить в виде суммы более простых сигналов. В частности, в виде суммы простейших гармонических колебаний, что выполняется при помощи преобразования Фурье.
Рассматривая функцию f(t1, t2,…tn) как элемент некоторого пространства функций, можно провести ее разложение в базисе этого пространства [3].
Разложение (анализ) сигнала отражает общий подход к исследованию физического объекта x путем его представления в виде суммы элементарных блоков xi: x=Sxi. Для сигналов или изображений это могут быть гармонические функции (базис Фурье-анализа), гармонические функции вида sin(x)/x (базис Шеннона-Котельникова), прямоугольные функции (базис Хаара), некоторые функции специального вида (вейвлет-анализ) [7].
В общем случае, базисом бесконечномерного линейного пространства Â, на котором определено понятие скалярного произведения функций (векторов), т.е. Гильбертова пространства, называется набор линейно независимых функций (векторов) {vi}такой, что для любой fÎÂ существует единственная линейная комбинация векторов {vi} [5]
f=c1v1+c2v2+…+cnvn+… (2.5.1)
где {сi} - коэффициенты разложения, vi - компоненты базиса, указывающие направление в пространстве.
Коэффициенты разложения определяются как скалярное произведение сигнала f и базисных функций:
сi=<f,vi> (2.5.2)
и (1) можно переписать в виде:
f=Si(<f,vi>vi) (2.5.3)
В том случае, если исследуемый сигнал аппроксимируется кусочно-непрерывной дифференцируемой функцией, т.е. отвечает условиям известной теоремы Дирихле, для f(t1, t2,…tn) существует преобразование Фурье – разложение в базисе комплексной экспоненты. Соответственно, математически разложение сигнала на гармонические составляющие описывается функциями значений амплитуд и начальных фаз колебаний по непрерывному или дискретному аргументу – частоте изменения функций на определенных интервалах аргументов их динамического представления. Совокупность амплитуд гармонических колебаний разложения называют амплитудным спектром сигнала, а совокупность начальных фаз – фазовым спектром. Оба спектра вместе образуют полный частотный спектр сигнала, который по точности математического представления тождественен динамической форме описания сигнала.
Общей целью при применении разложения по базису является представление сигнала в виде, удобном для исследования и обработки, а также приближение представления сигнала к оптимальному путем минимизации числа компонент разложения при максимальном качестве аппроксимации. Очевидно, что результативность применения определенного набора базисных функций зависит от природы сигнала. Главное условие допустимости разложения - ортогональность базисных функций. Но при качественном анализе сигналов могут применяться и неортогональные (биортогональные) функции, выявляющие какие-либо характерные особенности сигналов, полезные для интерпретации физических данных [6].
Линейные системы преобразования сигналов описываются дифференциальными уравнениями, причем для них верен принцип суперпозиции, согласно которому реакция систем на сложный сигнал, состоящий из суммы простых сигналов, равна сумме реакций от каждого составляющего сигнала в отдельности [5]. Это позволяет при известной реакции системы на гармоническое колебание с определенной частотой определить реакцию системы на любой сложный сигнал, разложив его в ряд гармоник по частотному спектру сигнала. Широкое использование гармонических функций при анализе сигналов объясняется тем, что они являются достаточно простыми ортогональными функциями и определены при всех значениях непрерывных переменных. Кроме того, они являются собственными функциями времени, сохраняющими свою форму при прохождении колебаний через любые линейные системы и системы обработки данных с постоянными параметрами (изменяются только амплитуда и фаза колебаний) [5].
Примеры частотного представления сигналов приводятся ниже (рис. 2.5 – 2.12).
2.6 Классификация сигналов [2]
Классификация осуществляется на основании существенных признаков соответствующих математических моделей сигналов.Все сигналы разделяют на две крупных группы: детерминированные и случайные (рис.2.4).

Рис. 2.4. Классификация сигналов.
Обычно выделяют два класса детерминированных сигналов: периодические и непериодические.
К периодическим относят гармонические и полигармонические сигналы. Для периодических сигналов выполняется общее условие s(t) = s(t + kT), где k = 1, 2, 3, ... - любое целое число, Т - период, являющийся конечным отрезком независимой переменной.

 Рис. 2.5. Гармонический сигнал и его спектр
Рис. 2.5. Гармонический сигнал и его спектр
|
Гармонические сигналы(или синусоидальные), описываются следующими формулами:
s(t) = A×sin (2pfоt+f) = A×sin (wоt+f), (2.6.1)
s(t) = A×cos(wоt+j),
где А, fo, wo, j, f - постоянные величины, которые могут исполнять роль информационных параметров сигнала: А - амплитуда сигнала, fо - циклическая частота в герцах, wо = 2pfо - угловая частота в радианах, j и f- начальные фазовые углы в радианах. Период одного колебания T = 1/fо = 2p/wo. При j = f-p/2 синусные и косинусные функции описывают один и тот же сигнал. Частотный спектр сигнала представлен амплитудным и начальным фазовым значением частоты fо (при t = 0).
Полигармонические сигналы составляют наиболее широко распространенную группу периодических сигналов и описываются суммой гармонических колебаний:
s(t) =  An sin (2pfnt+jn), (2.6.2)
An sin (2pfnt+jn), (2.6.2)
или непосредственно функцией s(t) = y(t ± kTp), k = 1,2,3,..., где Тр - период одного полного колебания сигнала y(t), заданного на одном периоде. Значение fp =1/Tp называют фундаментальной частотой колебаний. Полигармонические сигналы представляют собой сумму определенной постоянной составляющей (fо=0) и произвольного (в пределе - бесконечного) числа гармонических составляющих с произвольными значениями амплитуд An и фаз jn, с периодами, кратными периоду фундаментальной частоты fp. Другими словами, на периоде фундаментальной частоты fp, которая равна или кратно меньше минимальной частоты гармоник, укладывается кратное число периодов всех гармоник, что и создает периодичность повторения сигнала. Частотный спектр полигармонических сигналов дискретен, в связи с чем второе распространенное математическое представление сигналов - в виде спектров (рядов Фурье).
В качестве примера на рис. 2.6 приведен отрезок периодической сигнальной функции, которая получена суммированием постоянной составляющей (частота постоянной составляющей равна 0) и трех гармонических колебаний с разными значениями частоты и начальной фазы колебаний. Математическое описание сигнала задается формулой:
s(t) =  Ak×cos(2×p×fk×t+jk),
Ak×cos(2×p×fk×t+jk),
где: Ak = {5, 3, 4, 7} - амплитуда гармоник; fk = {0, 40, 80, 120} - частота в герцах; jk = {0, -0.4, -0.6, -0.8} - начальный фазовый угол колебаний в радианах; k = 0, 1, 2, 3. Фундаментальная частота сигнала 40 Гц.

Рис. 2.6. Модель сигнала.

Рис. 2.7. Спектр сигнала.
Частотное представление данного сигнала (спектр сигнала) приведено на рис. 2.7. Обратим внимание, что частотное представление периодического сигнала s(t), ограниченного по числу гармоник спектра, составляет всего восемь отсчетов и весьма компактно по сравнению с временным представлением.
Периодический сигнал любой произвольной формы может быть представлен в виде суммы гармонических колебаний с частотами, кратными фундаментальной частоте колебаний fр = 1/Тр. Для этого достаточно разложить один период сигнала в ряд Фурье по тригонометрическим функциям синуса и косинуса с шагом по частоте, равным фундаментальной частоте колебаний Df = fp:
s(t) =  (ak cos 2pkDft + bk sin 2pkDft), (2.6.3)
(ak cos 2pkDft + bk sin 2pkDft), (2.6.3)
ao = (1/T)  s(t) dt, ak = (2/T)
s(t) dt, ak = (2/T)  s(t) cos 2pkDft dt, (2.6.4)
s(t) cos 2pkDft dt, (2.6.4)
bk = (2/T)  s(t) sin 2pkDft dt. (2.6.5)
s(t) sin 2pkDft dt. (2.6.5)
Количество членов ряда Фурье K = kmax обычно ограничивается максимальными частотами fmax гармонических составляющих в сигналах так, чтобы fmax < K·fp. Однако для сигналов с разрывами и скачками имеет место fmax ® ¥ , при этом количество членов ряда ограничивается по допустимой погрешности аппроксимации функции s(t).
Одночастотные косинусные и синусные гармоники можно объединить и представить разложение в более компактной форме:
s(t) =  Sk cos (2pkDft-jk),
Sk cos (2pkDft-jk),
Sk =  , jk = argtg (bk/ak). (2.6.6)
, jk = argtg (bk/ak). (2.6.6)

Рис. 2.8. Прямоугольный периодический сигнал (меандр).
Пример представления прямоугольного периодического сигнала (меандра) в виде амплитудного ряда Фурье в частотной области приведен на рис. 2.8. Сигнал четный относительно t=0, не имеет синусных гармоник, все значения jk для данной модели сигнала равны нулю.
Информационными параметрами полигармонического сигнала могут быть как определенные особенности формы сигнала (размах от минимума до максимума, экстремальное отклонение от среднего значения, и т.п.), так и параметры определенных гармоник в этом сигнале. Так, например, для прямоугольных импульсов информационными параметрами могут быть период повторения импульсов, длительность импульсов, скважность импульсов (отношение периода к длительности). При анализе сложных периодических сигналов информационными параметрами могут также быть:
Текущее среднее значение за определенное время, например, за время периода:
(1/Т)  s(t) dt.
s(t) dt.
- Постоянная составляющая одного периода:
(1/Т)  s(t) dt.
s(t) dt.
- Среднее выпрямленное значение:
(1/Т)  |s(t)| dt.
|s(t)| dt.
- Среднее квадратичное значение:
 .
.
К непериодическим сигналам относят почти периодические и апериодические сигналы. Основным инструментом их анализа также является частотное представление.

Рис. 2.9. Почти периодический сигнал и спектр его амплитуд.
Почти периодические сигналы близки по своей форме к полигармоническим. Они также представляют собой сумму двух и более гармонических сигналов (в пределе – до бесконечности), но не с кратными, а с произвольными частотами, отношения которых (хотя бы двух частот минимум) не относятся к рациональным числам, вследствие чего фундаментальный период суммарных колебаний бесконечно велик. Так, например, сумма двух гармоник с частотами 2fo и 3.5fo дает периодический сигнал (2/3.5 – рациональное число) с фундаментальной частотой 0.5fo, на одном периоде которой будут укладываться 4 периода первой гармоники и 7 периодов второй. Но если значение частоты второй гармоники заменить близким значением  fo, то сигнал перейдет в разряд непериодических, поскольку отношение 2/
fo, то сигнал перейдет в разряд непериодических, поскольку отношение 2/  не относится к числу рациональных чисел. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.
не относится к числу рациональных чисел. Как правило, почти периодические сигналы порождаются физическими процессами, не связанными между собой. Математическое отображение сигналов тождественно полигармоническим сигналам (сумма гармоник), а частотный спектр также дискретен.
Апериодические сигналы составляют основную группу непериодических сигналов и задаются произвольными функциями времени. На рис. 2.10 показан пример апериодического сигнала, заданного формулой на интервале (0, ¥):
s(t) = exp(-a×t) - exp(-b×t),
где a и b – константы, в данном случае a = 0.15, b = 0.17.


Рис. 2.10. Апериодический сигнал и модуль спектра.
Рис. 2.11. Импульсный сигнал и модуль спектра.
К апериодическим сигналам относятся также импульсные сигналы, которые в радиотехнике и в отраслях, широко ее использующих, часто рассматривают в виде отдельного класса сигналов. Импульсы представляют собой сигналы, как правило, определенной и достаточно простой формы, существующие в пределах конечных временных интервалов. Сигнал, приведенный на рис. 2.11, относится к числу импульсных.
Частотный спектр апериодических сигналов непрерывен и может содержать любые гармоники в частотном интервале [0, ¥]. Для его вычисления используется интегральное преобразование Фурье, которое можно получить переходом в формулах (1.3) от суммирования к интегрированию при Df ® 0 и kDf ® f.
s(t) =  (a(f) cos 2pft + b(f) sin 2pft) df =
(a(f) cos 2pft + b(f) sin 2pft) df =  S(f) cos(2pft-j(f)) df. (2.6.7)
S(f) cos(2pft-j(f)) df. (2.6.7)
a(f) =  s(t) cos 2pft dt, b(f) =
s(t) cos 2pft dt, b(f) =  s(t) sin 2pft dt, (2.6.8)
s(t) sin 2pft dt, (2.6.8)
S(f) =  , j(f) = argtg (b(f)/a(f)). (2.6.9)
, j(f) = argtg (b(f)/a(f)). (2.6.9)
Частотные функции a(f), b(f) и S(f) представляют собой не амплитудные значения соответствующих гармоник на определенных частотах, а распределения спектральной плотности амплитуд этих гармоник по частотной шкале. Формулы (2.6.8-2.6.9) обычно называют формулами прямого преобразования Фурье, формулы (2.6.7) – обратного преобразования.
Если нас не интересует поведение сигнала за пределами области его задания [0, Т], то эта область может восприниматься, как один период периодического сигнала, т.е. значение Т принимается за фундаментальную частоту периодический колебаний, при этом для частотной модели сигнала может применяться разложение в ряды Фурье по области его задания (2.6.3-2.6.6).
В классе импульсных сигналов выделяют подкласс радиоимпульсов. Пример радиоимпульса приведен на рис. 2.12.

Рис. 2.12. Радиоимпульс и модуль его спектра.
Уравнение радиоимпульса имеет вид:
s(t) = u(t) cos(2pfot+jo).
где cos(2pfot+jo) – гармоническое колебание заполнения радиоимпульса, u(t) – огибающая радиоимпульса. Положение главного пика спектра радиоимпульса на частотной шкале соответствует частоте заполнения fo, а его ширина определяется длительностью радиоимпульса. Чем больше длительность радиоимпульса, тем меньше ширина главного частотного пика.
Все сигналы также можно разделить на два класса: с ограниченной (конечной) энергией и с бесконечной энергией.
Для сигналов с ограниченной энергией (иначе – сигналов с интегрируемым квадратом) должно выполняться соотношение:
 |s(t)|2dt < ∞.
|s(t)|2dt < ∞.
Как правило, к этому классу сигналов относятся апериодические и импульсные сигналы, не имеющие разрывов 2-го рода при ограниченном количестве разрывов 1-го рода []. Любые периодические, полигармонические и почти периодические сигналы, а также сигналы с разрывами и особыми точками 2-го рода, уходящими в бесконечность, относятся к сигналам с бесконечной энергией. Для их анализа применяются специальные методы.
Иногда в отдельный класс выделяют сигналы конечной длительности, отличные от нуля только на ограниченном интервале аргументов (независимых переменных). Такие сигналы обычно называют финитными.
2.7 Классификация случайных сигналов [2]
Случайным сигналом называют функцию времени, значения которой заранее неизвестны, и могут быть предсказаны лишь с некоторой вероятностью. Случайный сигнал отображает случайное физическое явление или физический процесс, причем зарегистрированный в единичном наблюдении сигнал не воспроизводится при повторных наблюдениях и не может быть описан явной математической зависимостью. При регистрации случайного сигнала реализуется только один из возможных вариантов (исходов) случайного процесса, а достаточно полное и точное описание процесса в целом можно произвести только после многократного повторения наблюдений и вычисления определенных статистических характеристик ансамбля реализаций сигнала. В качестве основных статистических характеристик случайных сигналов принимают:
а) закон распределения вероятности нахождения величины сигнала в определенном интервале значений;
б) спектральное распределение мощности сигнала.
Случайные сигналы подразделяют на стационарные и нестационарные. Случайные стационарные сигналы сохраняют свои статистические характеристики в последовательных реализациях случайного процесса. Что касается случайных нестационарных сигналов, то их общепринятой классификации не существует. Как правило, из них выделяют различные группы сигналов по особенностям их нестационарности.
3 3. Виды сигналов [3]
Выделяют следующие виды сигналов, которым соответствуют определенное математическое описание.
Аналоговый сигнал
 Рис. 3.1. Аналоговый сигнал.
Рис. 3.1. Аналоговый сигнал.
|
Аналоговый сигнал (analog signal) является непрерывной функцией непрерывного аргумента, т.е. определен для любого значения аргументов. Источниками аналоговых сигналов, как правило, являются физические процессы и явления, непрерывные в динамике своего развития во времени, в пространстве или по любой другой независимой переменной, при этом регистрируемый сигнал подобен (“аналогичен”) порождающему его процессу. Пример математической записи сигнала: y(t) = 4.8 exp[-(t-4)2/2.8] (Рис. 3.1), при этом как сама функция, так и ее аргументы, могут принимать любые значения в пределах некоторых интервалов y1 £ y £ y2, t1 £ t £ t2. Множество возможных значений сигнала образует континуум - непрерывное пространство, в котором любая сигнальная точка может быть определена с точностью до бесконечности. Примеры сигналов, аналоговых по своей природе - изменение напряженности электрического, магнитного, электромагнитного поля во времени и в пространстве.
Дискретный сигнал
Дискретный сигнал (discrete signal) (Рис. 3.2) по своим значениям также является непрерывной функцией, но определенной только по дискретным значениям аргумента.

Рис. 3.2 Дискретный сигнал
По множеству своих значений он является конечным (счетным) и описывается дискретной последовательностью отсчетов (samples) y(nDt), где y1 £ y £ y2, Dt - интервал между отсчетами (интервал или шаг дискретизации, sample time), n = 0, 1, 2,...,N. Величина, обратная шагу дискретизации: f = 1/Dt, называется частотой дискретизации (sampling frequency). Если дискретный сигнал получен дискретизацией (sampling) аналогового сигнала, то он представляет собой последовательность отсчетов, значения которых в точности равны значениям исходного сигнала по координатам nDt.
Пример дискретизации аналогового сигнала, приведенного на рис. 3.1, представлен на рис. 3.2.
Цифровой сигнал

Рис. 3.3. Цифровой сигнал
Цифровой сигнал (digital signal) квантован по своим значениям и дискретен по аргументу. Он описывается квантованной решетчатой функцией yn = Qk[y(nDt)], где Qk - функция квантования с числом уровней квантования k, при этом интервалы квантования могут быть как с равномерным распределением, так и с неравномерным, например - логарифмическим. Задается цифровой сигнал, как правило, в виде дискретного ряда (discrete series) числовых данных - числового массива по последовательным значениям аргумента при Dt = const, но в общем случае сигнал может задаваться и в виде таблицы для произвольных значений аргумента.
Цифровой сигнал конечен по множеству своих значений. Процесс преобразования бесконечных по значениям аналоговых отсчетов в конечное число цифровых значений называется квантованием по уровню, а возникающие при квантовании ошибки округления отсчетов (отбрасываемые значения) – шумами или ошибками квантования.
4 Преобразования сигналов [2],[3]
На разных этапах процессов получения и обработки информации материальное представление сигналов в устройствах регистрации и обработки, а также формы их математического описания при анализе данных, могут изменяться путем соответствующих операций преобразования типа сигналов.
Дискретизация сигналов
Дискретизация (discretization) осуществляет преобразование аналоговых сигналов (функций), непрерывных по аргументу, в функции мгновенных значений сигналов по дискретному аргументу. Дискретизация обычно производится с постоянным шагом по аргументу (равномерная дискретизация), при этом s(t) Þ s(nDt), где значения s(nDt) представляют собой отсчеты функции s(t) в моменты времени t = nDt, n = 0, 1, 2,..., N. Частота, с которой выполняются замеры аналогового сигнала, называется частотой дискретизации. В общем случае, сетка отсчетов по аргументу может быть произвольной, как, например, s(t) Þ s(tk), k=1, 2, …, K, или задаваться по определенному закону. В результате дискретизации непрерывный (аналоговый) сигнал переводится в последовательность чисел.
Квантование
Операция квантования или аналого-цифрового преобразования (АЦП; Analog-to-Digital Converter, ADC) заключается в преобразовании дискретного сигнала s(tn) в цифровой сигнал s(n) = sn » s(tn), n = 0, 1, 2,.., N, как правило, кодированный в двоичной системе счисления. Процесс преобразования отсчетов сигнала в числа называется квантованием по уровню (quantization), а возникающие при этом потери информации за счет округления – ошибками или шумами квантования (quantization error, quantization noise).
При преобразовании аналогового сигнала непосредственно в цифровой сигнал операции дискретизации и квантования совмещаются.