Отношения эквивалентности и порядка. Связь разбиения множества на классы с эквивалентностью

Лекция 3. Отношения

3.1..Декартово произведение множеств.

3.2.Отношения. Бинарные отношения. Свойства бинарных отношений.

3.3.Отношения эквивалентности и порядка. Связь разбиения множества на классы с эквивалентностью

 

Программные положения

Отношения можно рассматривать как часть теории множеств. Описание выделения групп объектов внутри множества, разбиение множества на классы (непересекающиеся группы) крайне важно как в математике, так и в психологии.

 

 

Методические рекомендации к изучению лекции

Обратите внимание на различие между математическим и «бытовым» понятием отношения. Обратите внимание, что в математике отношение – это не столько взаимодействие между объектами, сколько подмножество некоторого декартового произведения

 

 

Литература

А.В.Дорофеева «Высшая математика. Гуманитарные специальности» Глава 1, п. 1.8.-1.10

 

Дополнительно:

 

Контрольные вопросы

1. Что такое декартово произведение множеств? Сколько элементов (исходные множества конечны) оно содержит?
2. Опишите декартово произведение множеств А={a,b,c} B={x,y,z}. Сколько элементов оно содержит?
3. Найдите область определения и множество значений отношения {(1,2), (2,4), (3,6),…}
4. Пусть А = {(b, а), (с, е), (d, i), (f, о){g, u)} и
5. В = {(v, а), (w, е), (х, i), (у, о)(z, u)}.

а) Опишите отношения А^-1 и В^-1

в) Опишите отношение А^-1 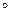В.

г) Опишите отношение В^-1 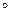А.

6. Опишите разбиение множества целых чисел на классы с помощью отношения «разность чисел делится на 6»

 

Декартово произведение множеств

 

Определение 3.1.

Декартовым произведением множеств X и Y называется множество упорядоченных пар (x,y) таких, что x – элемент из множества X, y – элемент множества Y .

Обозначается декартово произведение X Y

 

Замечание 3.1.

Декартово произведение – множество упорядоченных пар и , вообще говоря,

X Y Y X

 

Пример 3.1.

X={1,2,3}, Y={#,*}

X Y = {(1,#), (1,*), (2,#), (2,*), (3,#), (3,*)}

Y X = {(#,1), (#,2), (#,3), (*,1), (*,2), (*,3)}

 

Если каждое из множеств А и В представляет собой множество действительных чисел, то А В представляет собой декартову плоскость, на которой упорядоченные пары чисел используются для графического изображения функций.

Если А содержит m элементов, а В содержит n элементов, тогда А В содержит mn элементов. В частности, если А пусто или В пусто, то, по определению, А В пусто.

 

 

Отношения. Бинарные отношения. Свойства бинарных отношений.

 

Определение 3.2(1)

Отношением R (от “Relation” – отношение) множеств А и В называется произвольное подмножество A B. Если (а, b) R, это записывают как aRb, при этом говорят, что а и b находятся в отношении R, или просто, что а относится к b. Иногда для обозначения отношения вместо заглавных латинских букв используются греческие, а также различные специальные значки, например, a b или a b

 

Пример 3.2 (1)

1)Все множество A B есть отношение множеств А и В

2)Если А = {1,2,3}, а В = {*, #}, так что A B = { (1, *), (2,*), (3,*), (1,#), (2,#), (3,#)},

тогда пусть R = {(l,*), (l,#), (3,#)} есть отношение множеств А и В. Можно также записать 3R#, поскольку (3,#) R. Множество A B содержит шесть элементов, поэтому существует 2⁶ = 64 подмножества множества A B. Следовательно, существует 64 различных отношений на A B.

 

Определение 3.2. (2)

Если А = В, то отношение есть подмножество A A такое отношение называют бинарным отношением на А. В дальнейшем мы будем рассматривать такие отношения

 

Примеры 3.2 (2).

1). Отношения на множестве натуральных чисел N:

- отношение выполняется для пар (7,9) и (7,7), но не выполняется для пары (9,7);

- отношение «иметь общий делитель, отличный от единицы», выполняется для пар (6,9), (4,2), (2,4), (4,4), но не выполняется для пар (7, 9) и (9, 7);

- отношение «быть делителем» (т. е. aRb означает «а — делитель b») выполняется для пар (2, 4) и (4, 4), но не выполняется для пар (4, 2) и (7, 9).

2). Отношения на множестве точек действительной плоскости:

- отношение «находиться на одинаковом расстоянии от начала координат» выполняется для пары точек (3, 4) и (—2, 1/21), но не выполняется для пары точек (3, 4) и (1, 6); это отношение совпадает с отношением «находиться на одной и той же окружности с центром в начале координат»;

- отношение «находиться на разном расстоянии от начала координат» выполняется для тех и только тех пар точек, для которых не выполняется предыдущее отношение;

- отношение «быть симметричным относительно оси x» выполняется для всех пар точек (х₁, у₁) и (х₂, у₂), удовлетворяющих условию х₁ = х₂, у₁ = -у₂.

3). Отношения на множестве людей:

«жить в одном городе»; «быть моложе»; «быть сыном»; «быть знакомым».

 

Определение 3.2.(3).

Область определения отношения R на А и В есть множество всех х А таких, что для некоторых у В имеем (х,у) R. Другими словами, область определения R есть множество всех первых координат упорядоченных пар из R. Множество значений отношения R на А и В есть множество всех у В таких, что (х, у) R для некоторого

х А. Другими словами, множество значений R есть множество всех вторых координат

упорядоченных пар из R.

 

Определение 3.2.(4)

С каждым отношением R на А В связано отношение R^-1 на В А. Пусть R А В есть отношение на А В. Тогда отношение R^-1 на В А определяется следующим образом: R^-1= {(b,a) : (a,b) R}

Другими словами, (b, а) R^-1 тогда и только тогда, когда (a, b) R или, что

равносильно, b R^-1a тогда и только тогда, когда aRb. Отношение R^-1 называется обратным отношением к данному отношению R.

Примеры 3.2. (4)

1) Пусть R = {(l,*), (l,#), (3,#)}, тогда R^-1 = {(*, 1), (#,1), (#,3)}.

2)Пусть R - отношение {(х,у) : у является родственником х}, тогда R^-1 = R

 

 

Определение 3.2.(5)

Пусть R А В – отношение R на А В, а S B C - отношение S на B C.

Композицией отношений S и R называется отношение T A C, определенное таким образом:

T = {(a,c) : существует такой элемент b из B, что (a,b) R и (b, c) R}

Такое множество T обозначается T = S 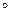R

 

Примеры 3.2.(5)

1) Пусть A={1,2,3} , B={#,*}, C={w,x,y,z} и пусть отношения

R на А В и S B C заданы так:

R={(1,#), (1,*),(3,#)}

S={(#,w), (#,x), (*,y), (*,z)}

 

 

T A C = S 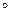R = {(1,w), (1,x), (1,y), (1,z), (3,w), (3,x)}

Поскольку

из (1,#) R и (#,w) S следует (1,w) S R

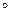(1,#) R и (#,x) S следует (1,x) S R

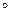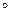(1,*) R и (*,y) S следует (1,y) S R

и так далее

 

2) Пусть R и S – бинарные отношения на множестве положительных целых чисел, заданные таким образом: S = {(x, x+2) : x – положительное число} и R = {(x, x⁴ ): x – положительное целое число} и S 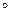R = {(x, x⁴ +2) : x – положительное целое число} и

R 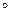S = {(x, (x+2)⁴ ) : x – положительное целое число}.

 

Определения 3.2.(6)

 

Отношение R на А А называется рефлексивным, если (а, а) принадлежит R для всех а из А.

Отношение R называется антирефлексивным, если из (а, b) R следует а b.

Отношение R симметрично, если для всех а и b, принадлежащих А, из (а, b) R следует, что (b,a) R.

Отношение R транзитивно, если для всех а, b и с из А из того, что (а, b) R и (b,c) R, следует, что (а, c) R.

Отношение R называется антисимметричным, если для всех а и b из A, из принадлежности (а, b) и (b, а) отношению R следует, что а = b.

 

Пример 3.2.(6)

Пусть А = {1,2,3,4} и пусть отношение R₁ А А есть множество

R₁ = {(1,1), (2,2), (3,3), (4,4), (1,2), (1,4), (2,1), (4,1)}.

Отношение R₁ рефлексивно, т.к. для каждого а А, (а,а) R₁. Рассмотрев все возможные случаи и показав, что в каждом из них из (a,b) R₁ следует (b,а) R₁, можно показать, что отношение R₁ является симметричным, транзитивным, но не антисимметричным

 

Отношения эквивалентности и порядка. Связь разбиения множества на классы с эквивалентностью

 

Определение 3.3.(1)

Отношение R на А есть отношение эквивалентности, если оно рефлексивно, симметрично и транзитивно.

Пример 3.3.(1)

Пусть А — множество целых чисел. Определим отношение R₂ А А таким образом:

R₂ = {(а, b) : а - b = 5 • к для некоторого целого числа к}(разность чисел a и b делится на 5).

Например, (8,3) R₂, поскольку 8-3 = 5 = 5•1, и (-11,4) R₂, так как

(-11)-4 = -15 = 5• (-3).

Отношение R₂ рефлексивно. Если а — целое число (т.е. а А), то а — а = 0 = 5 • 0 = 5 • к для к = 0, так что (а, а) R₂.

Отношение R₂ симметрично. Допустим, (а, b) R₂. Тогда существует такое целое число t, что а — b = 5 • t и b — а = — (а — b) = — (5t) = 5(—t) для целого числа (—t). Таким образом, (b, а) R₂

Отношение R₂транзитивно. Предположим, что a, b и с — целые числа, (а, b) R₂ и

(b, c) R₂.

Если (а, b) R₂, то a – b = 5k для некоторого k,

Если (b,c) R₂, то b – c = 5m для некоторого m.

Если сложить левые и правые части этих равенств, мы получим (a – b) + (b – c) = 5k + 5m = (a – c) = 5(k+m), (k+m) целое.

 

Таким образом, отношение R₂ – есть отношение эквивалентности

 

Разбиение на классы.

В самых различных вопросах встречаются разбиения тех или иных множеств на попарно непересекающиеся подмножества. Например, плоскость (рассматриваемую как множество точек) можно разбить на прямые, параллельные оси ж, трехмерное пространство можно

представить как объединение концентрических сфер различных радиусов (начиная с r = 0), жителей данного города можно разбить на группы по их году рождения и т. п.

 

Определение 3.3.(2)

Каждый раз, когда некоторое множество A представлено тем или иным способом как сумма попарно непересекающихся подмножеств, мы говорим о разбиении множества A на классы.

Обычно приходится иметь дело с разбиениями, построенными на базе того или иного признака, по которому элементы множества A объединяются в классы. Например, множество всех треугольников на плоскости можно разбить на классы равных между собой или на классы равновеликих треугольников, все функции от х можно разбить на классы, собирая в один класс функции, принимающие в данной точке одинаковые значения, и т. д.

Признаки, по которым элементы множества разбиваются на классы, могут быть самыми разнообразными. Но все же такой признак не вполне произволен. Предположим, например, что мы захотели бы разбить все действительные числа на классы, включая число b в тот же класс, что и число а, в том и только в том случае, когда b > а.

Ясно, что никакого разбиения действительных чисел на классы таким путем получить нельзя, так как если b > а, т. е. если b следует зачислить в тот же класс, что и а, то а < b, т. е. число а нельзя включить в тот же класс, что и b. Кроме того, так как а не больше, чем само а, то а не должно попасть в один класс с самим собой.

Другой пример. Попробуем разбить точки плоскости на классы, относя две точки к одному классу в том и только том случае, когда расстояние между ними меньше 1. Ясно, что добиться этого нельзя, так как если расстояние от а до b меньше 1 и расстояние от b до с меньше 1, то это вовсе не означает, что расстояние от а до с меньше 1. Таким образом, зачисляя а в один класс с b, а b в один класс с с, мы получим, что в один и тот же класс могут попасть две точки, расстояние между которыми больше 1.

Теорема 3.3.(6)

Три условия эквивалентности необходимы и достаточны, чтобы дать возможность разбить А на классы.

Доказательство:

Всякое разбиение данного множества на классы определяет между элементами этого множества некоторое отношение эквивалентности. Действительно, если аRb означает «а находится в том же классе, что и b», то отношение R будет рефлексивным, симметричным и транзитивным.

И наоборот, пусть R — некоторое отношение эквивалентности между элементами множества А и Ка — класс элементов х из А, эквивалентных данному элементу а: хRа. В силу свойства рефлексивности элемент а сам принадлежит классу Ка. Покажем, что два

класса Ка и Кb либо совпадают, либо не пересекаются. Пусть некоторый элемент с принадлежит одновременно и Ка, и Кb, т.е. сRа и сRb. Тогда в силу симметричности аRс и в силу транзитивности аRb. Если теперь х — произвольный элемент из Ка, т. е. xRа, то в силу aRb и свойства транзитивности хRb, т. е. х Кb.

Точно так же доказывается, что всякий элемент у Кb входит в Ка. Таким образом, два класса Ка и Кb, имеющих хотя бы один общий элемент, совпадают между собой. Мы получили разбиение множества A на классы по заданному отношению эквивалентности.

 

Таким образом, отношение эквивалентности R на множестве А разбивает его на подмножества, элементы которых эквивалентны друг другу и не эквивалентны элементам

других подмножеств. Эти подмножества называются классами эквивалентности по отношению R.

Это разбиение можно представлять себе следующим образом. Пусть множество А — это набор разноцветных шаров, а отношение R задается условием:

(а, b) R тогда и только тогда, когда а и b имеют одинаковый цвет. Поскольку R — отношение эквивалентности, каждый класс эквивалентности будет состоять из шаров, имеющих одинаковый цвет. Если определить отношение R условием:

(а, b) R тогда и только тогда, когда шары а и b имеют одинаковый диаметр, то каждый класс эквивалентности будет состоять из шаров одинакового размера.

Вернемся к примеру 3.5.(6)

Пусть [a] = {x: (x, a) R₂} = {x: x R₂ a} = {x: x – a =5k для некоторого целого k} =

= {x: x = a+5k для некоторого целого k}

 

Получаем разбиение на классы (элементы одного класса имеют один и тот же остаток при делении на 5):

[0] = {…, - 15, - 10, - 5, 0 , 5, 10, 15, 20, …}

[1] = {…, - 14, - 9, - 4, 1, 6, 11, …}

[2] = {…, - 13, - 8, - 3, 2, 7, 12, …}

[3] = {…, - 12, - 7, - 2, 3, 8, 13, …}

[4] = {…, - 11, - 6, - 1, 4, 9, 14,…}

Таким образом, множество целых чисел с помощью отношения эквивалентности R₂ разбивается на 5 классов: [0], [1], [2], [3], [4].

 

Определение 3.3.(3)

Отношение называется отношением частичного порядка, если оно рефлексивно, антисимметрично и транзитивно. Таково, например, отношение , .

Если же отношение является антирефлексивным и транзитивным, оно называется отношением строгого порядка. Таковы, например, <, .