V. Список використаних джерел
Пальчех М. В.
Перевірила викладач к.к.н.
Назаренко Л. Д.
Суми 2011
План
I. Інформаційний огляд теми
II. Викладення методу
III. Реалізація методу на прикладі
· Програмна реалізація
· Пакетна реалізація
IV. Висновки і результати
V. Список використаних джерел
I. Інформаційний огляд теми
У великій кількості наук, таких як фізика, хімія, математика, економіка, оптимізація, теорія управління та ін. існує безліч задач, які пов’язані з чисельним інтегруванням. Чисельне інтегрування застосовується тоді, коли:
× Сама підінтегральна функція не задана аналітично. Наприклад, вона представлена у вигляді таблиці (масиву) значень у вузлах деякої розрахункової сітки.
× Аналітичне подання підінтегральної функції відомо, але її первісна не виражається через аналітичні функції. Наприклад,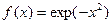 
.
До задач, які вирішує інтегрування, відносяться, як правило, задачі на знаходження площі, маси, щільності, об’єму, задачі, що пов’язані з простором великої розмірності (у теорії струн) , а також задачах, де є системи з багатьма степенями свободи.
Чисельне інтегрування – обчислення значення (як правило наближеного) визначеного інтеграла, засноване на тому, що величина інтеграла чисельно дорівнює площі криволінійної трапеції.
Задача полягає в заміні підінтегральної функції 
, для котрої важко або неможливо записати первісну у аналітиці, деякою апроксимуючою функцією 
Такою функцією зазвичай є кусочний поліном 
. Тобто 
, де 
- апріорна похибка методу на інтервалі інтегрування, а 
- апріорна похибка методу на окремому кроці інтегрування.
Кратний інтеграл або ж багатократний інтеграл степеня n, це визначений інтеграл по n змінних з функції n змінних:
.
Існує велика кількість методів чисельного обчислення кратних інтегралів. Ці методи називають кубатурними. Їх можна поділити на декілька груп:
× Методи Н’ютона-Котеса.
Тут 
- поліном різних степенів. До цієї групи відносять також метод Сімпсона, метод сіток.
× Методи статичних випробувань (Методи Монте-Карло).
Вузли сітки для кубатурного інтегрування вибираються за допомогою датчика випадкових чисел, відповідь носить імовірнісний характер. В основному застосовуються для обчислення кратних інтегралів. Цей метод дуже доречно використовувати при кратності інтеграла >3.
× Сплайнові методи.
Тут - кусковий поліном з умовами зв'язку між окремими поліномами за допомогою системи коефіцієнтів.
× Методи найвищої алгебраїчної точності.
Ці методи забезпечують оптимальну розстановку вузлів сітки інтегрування і вибір вагових коефіцієнтів 
в задачі 
. Сюди відноситься метод Гауса-Крістофеля (обчислення невласних інтегралів) і метод Маркова.
Мене дуже зацікавив метод чисельного інтегрування Монте-Карло тим, що за допомогою нього можна вирішити дуже складні задачі, пов’язані з інтегруванням функцій великої розмірності, задачі, які дуже складно вирішити іншими методами, так як їх використання не є доцільним із-за швидкого росту зростання числа точок сітки та/або складної границі інтегрування.
II. Викладення методу
Для того, щоб зрозуміти суть методу, потрібно розібратися в понятті математичного сподівання.
Математичне сподівання – міра середнього значення випадкової величини в теорії ймовірностей. Позначається як 
.
Метод Монте-Карло для обчислення інтегралів заклечається в генеруванні випадкових точок та усереднюванні значення функції в них.
Припустимо, потрібно обчислити визначений інтеграл 
. Розглянемо випадкову величину 
, рівномірно розподілену на відрізку інтегрування 
. Тоді 
так само буде випадковою величиною, причому її математичне сподівання виражається як 
, де 
- щільність розподілу випадкової величини 
, що дорівнює 
на ділянці .
Таким чином, шуканий інтеграл виражається як 
.
Але математичне очікування випадкової величини можна легко оцінити, змоделювавши цю випадкову величину і порахувавши вибіркове середнє.
Отже, кидаємо 
точок, рівномірно розподілених на , для кожної точки 
обчислюємо 
. Потім обчислюємо вибіркове середнє: 
.
У підсумку отримуємо оцінку інтеграла: 
.
Точність оцінки не залежить від вигляду підінтегральної функції чи від кратності інтегралу. Вона залежить тільки від кількості точок 
. Похибку методу розраховують за формулою 
Цю похибку можна зменшити, якщо збільшити кількість випробувань n або застосовуючи додатково деякі методи з теорії ймовірностей(методи істотної вибірки або випадкового
блукання).
Двукратні інтеграли будуть обчислюватись по формулі 
.
Інтеграли, кратність яких більше 2, будуть обчислюватись аналогічно.
III. Реалізація методу на прикладі
Для того, щоб зрозуміти практичну реалізацію методу, розглянемо його на прикладі
.
Алгоритм програми обчислення інтегралу буде таким:
1. Введення кількості випробувань n.
2. Запустити генератор випадкових чисел.
3. Визначення загальних меж інтегрування.
4. Випадковим чином (з урахуванням загальних меж інтегрування) генерувати значення x і y.
5. Якщо значення x і y лежать в поточних межах інтегрування, то до значення інтеграла додати значення функції при цих значеннях.
6. Пункти 4 та 5 повторити n разів.
7. Остаточно отриману суму з формули перемножити на решту частини формули для отримання значення інтеграла.
Вхідні дані : a = нижня границя інтегрування, b – верхняя границя інтегрування, chislo vyprobuvan – число випробувань.
Вихідні дані - Userednenyy integral – значення інтегралу.
· Програмна реалізація
program MonteCarlo;
uses
crt;
const k=100;
Var a,b,c,d,ng,vg,x,y,s,integral : real;
n,i,j : integer;
integr:array[1..k]of real;
Function f(x,y:real):real;
Begin
f:=Sqrt(x+y);
end;
Function nm(x:real):real;
Begin
nm:=3*x;
end;
Function vm(x:real):real;
Begin
vm:=8*x;
end;
BEGIN
clrscr;
writeln('Vvedit znachennya granyts integruvannya ');
write('a='); readln(a);
write('b='); readln(b);
writeln('Vvedit chyslo vyprobuvan:');
readln(n);
c:=nm(a);
d:=vm(b);
randomize;
for j:=1 to k do
begin
s:=0; integral:=0;
For i:=1 to n do
begin
x:=a+(b-a)*random;
y:=c+(d-c)*random;
ng:=nm(x);
vg:=vm(x);
If (y <= vg) and(y >= ng) then s:=s + f(x, y);
end;
integr[j]:=(b-a)*(d-c)*s/n;
writeln(integr[j]:10:4);
end;
for j:=1 to k do
Integral:=integral+ integr[j];
writeln('Userednenyy integral=',(integral/k):10:4);
readln;
END.
· Пакетна реалізація
Mathcad дозволяє обчислювати кратні інтеграли безпосередньо, однак у більшості випадків при кратності інтегралів 3 і більше застосування самого методу Монте-Карло переважно. Справа в тому, при однаковій точності метод Монте-Карло дає суттєвий виграш у часі (в десятки і сотні разів), особливо при великій кратності інтегралів.
IV. Висновoк
Існує багато завдань, для вирішення яких випадковий підхід більш ефективний, ніж інші математичні методи. Метод Монте-Карло застосовувався у багатьох завданнях, проте його використання не завжди було виправдано через великої кількості обчислень, необхідних для отримання відповіді із заданою точністю. Існує клас завдань, складність (кількість обчислень, необхідних для отримання точної відповіді) яких зростає з розмірністю задачі експоненціально. Іноді можна, пожертвувавши точністю, знайти алгоритм, складність якого зростає повільніше, але є велика кількість завдань, для якого цього не можна зробити і метод Монте-Карло є єдиною можливістю для отримання достатньо точної відповіді за прийнятний час.
Необхідність застосування чисельних методів, а саме методу Монте-Карло, частіше за все може бути викликана відсутністю у первісної функції подання в елементарних функціях і, отже, неможливістю аналітичного обчислення значення певного інтеграла. Також можлива ситуація, коли вид первообразной настільки складний, що швидше обчислити значення інтеграла чисельним методом.
Я реалізувала метод Монте-Карло в додатку BP, а також у пакеті Mathcad.
Mathcad дозволяє обчислювати кратні інтеграли безпосередньо, однак у більшості випадків при кратності інтегралів 3 і більше застосування самого методу Монте-Карло переважно. Справа в тому, при однаковій точності метод Монте-Карло дає суттєвий виграш у часі (в десятки і сотні разів), особливо при великій кратності інтегралів.
В даний час основні зусилля дослідників спрямовані на створення ефективних Монте-Карло алгоритмів різних фізичних хімічних і соціальних процесів для паралельних обчислювальних систем.
Метод Монте-Карло використовується дуже часто, часом некритично і неефективним чином. Має деякі очевидні переваги:
а) Він не вимагає ніяких пропозицій про регулярність, за винятком квадратичної інтегровності. Це може бути корисним, так як часто дуже складна функція, чиї властивості регулярності важко встановити.
б) Він призводить до здійсненним процедурі навіть у багатовимірному випадку, коли чисельне інтегрування не застосовується, наприклад, при числі вимірювань, більше 10.
в) Його легко застосовувати при малих обмеженнях або без попереднього аналізу завдання.
Він має, проте, деякі недоліки, а саме:
а) Межі похибки не визначені точно.
б) Статична похибка зменшується повільно.
в) Необхідність мати випадкові числа.