Расчет премий по рисковым видам страхования

В отечественной практике "рисковыми" называют виды страхования, "относящиеся к видам страховой деятельности иным, чем страхование жизни:

■ не предусматривающие обязательства страховщика по выплате страховой суммы при окончании срока действия договора страхования;

■ не связанные с накоплением страховой суммы в течение срока действия договора страхования" (Методика расчета тарифных ставок по рисковым видам страхования, утв. распоряжением Федеральной службы России по надзору за страховой деятельностью от 8 июля 1993 г. № 02-03-36).

Обязательства страховщика здесь связаны только с покрытием случайного риска. Срок страхования, как правило, не превышает одного года. Расчет рисковой премии строится на принципе эквивалентности в упрощенной формулировке, предусматривающий равенство ожидаемых стоимостей взаимных обязательств без учета возможного дохода от инвестирования временно свободных средств.

Рисковые виды страхования с точки зрения особенностей актуарных расчетов можно условно разделить на массовые виды и страхование редких событий и крупных рисков.

Под массовыми видами страхования понимаются "виды страхования, предположительно охватывающие значительное число субъектов страхования и страховых рисков, характеризующихся однородностью объектов страхования и незначительным разбросом в размерах страховых сумм" (см. указанную Методику). Благодаря указанным особенностям они хорошо подчиняются закону больших чисел. В качестве меры риска используют ожидаемые значения убытков. Массовыми рисковыми видами можно считать большинство видов страхования имущества и гражданской ответственности частных лиц, а также некоторые виды личного страхования (такие, как страхование от несчастного случая, страхование медицинских расходов и т.д.).

К страхованию редких событий и крупных рисков относится страхование событий, характеризующихся, с одной стороны, низкой вероятностью наступления, а с другой стороны - большой возможной величиной ущерба. При этом количество объектов, которые можно застраховать, обычно ограничено, а разброс страховых сумм и совокупного убытка составляет значительную величину. Уверенно использовать в такой ситуации ожидаемые значения для оценки "чистого" риска не представляется возможным. Даже один-два крупных страховых случая могут серьезно нарушить баланс премий и выплат в портфеле. Актуарные расчеты по страхованию редких событий и крупных рисков имеют свою специфику. Они требуют наличия информации о риске, собранной в течение длительного периода не одной компанией, а различными специальными организациями или объединениями страховщиков. Сложность определения адекватной цены страхования и возможность разбалансирования портфеля из-за одного страхового случая требуют обязательного применения дополнительных методов повышения финансовой устойчивости. Основными мерами являются перестрахование и объединение компаний в страховые пулы.

К страхованию редких событий и крупных рисков относятся страхование больших промышленных предприятий, авиационное и космическое страхование, страхование "атомных" рисков. Другим примером из данной категории является страхование на случай природных катастроф. Частота наступления страхового случая в конкретном регионе очень невелика (не более одного раза в несколько лет), а возможный ущерб весьма значителен. Причем огромная величина убытков здесь получается вследствие кумуляции повреждений или уничтожения множества мелких объектов, подвергшихся воздействию стихии.

Методы, используемые в актуарных расчетах по страхованию редких событий и крупных рисков, достаточно сложны и требуют глубоких математических знаний. Далее будут рассмотрены только принципиальные подходы к расчету тарифов по массовым рисковым видам страхования.

Пример. Рисковая премия при случайном размере убытка

В предыдущих примерах рассматривалась защита от риска хищения, где величина убытка по отдельному договору была неслучайна и равнялась стоимости автомобиля. Теперь предположим, что страхование осуществляется на случай ущерба при ДТП.

Повреждения автомобиля при аварии могут быть различны: от маленькой царапины на бампере до полного уничтожения. Поэтому выплата по страховому случаю S_B случайным образом принимает любое значение от 0 до максимально возможного убытка, равного стоимости объекта (а значит, и страховой сумме S). Закон распределения этой непрерывной случайной величины на интервале от 0 до S зависит от вида страхования и характеристик объекта. В страховании имущества от ущерба он часто имеет форму, представленную на рис. 5.3.

Для подобного закона распределения вероятность очень мелких (участок 1) и очень крупных ущербов (участок 3) мала. Большинство убытков попадает в окрестности ожидаемого (среднего) значения S_B (участок 2).

Если факт наступления страхового случая и размер убытка независимы (т.е. по информации о том, что страховой случай наступил, нельзя сделать выводов о величине предстоящей выплаты), то ожидаемая сумма выплат по договору может быть рассчитана как произведение вероятности случая q на ожидаемую величину выплаты S_B.

Следуя принципу эквивалентности, получаем выражение для рисковой премии:

Важным отличием данной формулы от соотношения, полученного в предыдущих примерах, является замена детерминированной выплаты s_B на ожидаемую величину выплаты при страховом случае S_u. Это произошло потому, что размер выплаты здесь является случайной величиной.

Рис. 5.3. Примерная форма распределения величины убытка при страховом случае по страхованию имущества

Таким образом, в общем случае для рисковых видов страхования можно записать

В некоторых видах страхования существует возможность наступления нескольких страховых случаев в течение периода действия договора. Тогда в выражении для расчета рисковой премии вместо вероятности будет использоваться ожидаемое число страховых случаев по договору, которое может принимать значения больше единицы:

Пример. Тариф для расчета рисковой премии

До настоящего момента в примерах рассматривался подход к определению рисковой премии для группы абсолютно одинаковых объектов, у которых степень риска и страховые суммы были одинаковы. Но в жизни характеристики объектов различны. Рассчитывать рисковую премию заново при заключении каждого договора исходя из конкретной степени риска и страховой суммы на практике неудобно. Поэтому объекты с близкими значениями вероятности и ожидаемой величиной выплаты объединяют в группы и рассчитывают для них единый тариф, отражающий относительный уровень риска в расчете на единицу страховой суммы. Премия для любого договора в группе определяется как произведение страховой суммы на этот тариф. Такой подход значительно сокращает объем вычислений и упрощает процесс определения цены страхования.

Лежащий в основе рисковой премии тариф в отечественной практике называется основная часть нетто-ставки и обозначается Т_o.

По определению, премия равна произведению страховой суммы на тариф. Тогда для рисковой премии П по договору со страховой суммой S можно записать

На момент расчета точные страховые суммы будущих договоров компании неизвестны, т.е. они являются случайными. Если пред-

полагается, что страховые суммы в группе будут иметь небольшой разброс относительно некоторой средней величины S, то при расчете тарифа вместо фактического значения можно использовать эту ожидаемую величину:

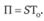
Стоимость обязательств страховщика равна произведению вероятности страхового случая на ожидаемый убыток (qS_B).

Применяя принцип эквивалентности и разделив обе части на S, получаем формулу для основной части нетто-ставки

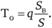
В полученном выражении отношение ожидаемой выплаты S_ti к ожидаемой страховой сумме S характеризует среднюю "тяжесть" страхового случая для данной совокупности договоров. Этот показатель является достаточно устойчивым для конкретного вида страхования (страхового продукта):

Формула для расчета основной части нетто-ставки соответствует общему случаю, когда случайными являются и факт наступления, и размер убытка. Нетрудно показать, что полученные в предыдущих примерах выражения для рисковой премии являются частными случаями применения данной формулы при детерминированных значениях S_B и S.