Процедуры факторного анализа

Следует отметить, что базовое уравнение факторного анализа (10.2) не имеет единственного решения, если одновременно требуется оценить и значения факторов, и их весовые коэффициенты – факторные нагрузки. Строго говоря, это уравнение имеет бесконечно много решений. Поэтому необходимо ввести несколько дополнительных соглашений, касающихся самой процедуры выделения факторов. В зависимости от того, какие конкретно допущения делаются, можно выделить следующие основные варианты факторного анализа:

1) диагональные и множественные групповые решения;

2) решения, основанные на выделении главных факторов;

3) конфирматорные решения, основанные на максимальном правдоподобии.

Первые два варианта решения принято относить к эксплораторным, т.е. разведочным, методам факторного анализа. Это наиболее часто встречающиеся в психологии варианты факторного анализа. Их назначение как раз и состоит в том, чтобы уменьшить неопределенность данных, дать исследователю способ их более компактного описания. Третий вариант факторного решения относится к конфирматорным. Его назначение – подтвердить или опровергнуть уже имеющиеся теоретические представления о структуре факторов. Этот метод напоминает методы проверки статистических гипотез, рассмотренные ранее. Именно поэтому его научная ценность оказывается выше. В то же время конфирматорные процедуры оказываются более сложными и требуют больших вычислительных усилий, связанных с обработкой большого объема данных. Они также накладывают более строгие по сравнению с эксплораторными процедурами ограничения на структуру исследуемых данных. Возможно, в этом заключается одна из причин того, что конфирматорный факторный анализ все еще недостаточно широко распространен в практике психологических исследований.

Диагональный анализ представляет собой наиболее простой из всех вариантов факторного анализа. Предполагается, что первый фактор является эквивалентом одной из исследуемых переменных. На основе такого предположения рассчитывается вклад этого фактора в общую систему корреляций анализируемых переменных. Затем оцененный вклад данного фактора извлекается из общей структуры корреляции, и определяется Вперед переменная, которая рассматривается в качестве эквивалента второго фактора. Процедура продолжается до тех пор, пока все интересующие исследователя факторы не будут извлечены.

Метод получил название диагонального, потому что в нем для оценки значений факторов используются диагональные элементы в матрице корреляций. Проблема, однако, состоит в том, чтобы определить, какая часть корреляции переменной с самой собой определяет ее как фактор, а какая определяет связь этой переменной с другими переменными. В простейшем случае за эту величину берут максимальное значение корреляции, равное единице. Тогда корреляции первого фактора с остальными переменными представляют собой корреляции рассматриваемой переменной с этими переменными.

Обобщением диагонального анализа является множественный групповой анализ. В этом случае факторы рассматриваются как композиция двух или более переменных. Одним из вариантов такого анализа является разработанный Л. Терстоном центроидный метод факторного анализа (L. Thurstone [27]).

Процедура центроидного метода достаточна проста и может быть реализована даже в "ручных" вычислениях (Я. Окунь [15]). Она предполагает переход от полной корреляционной матрицы к ее редуцированному варианту. В этой матрице в качестве диагональных элементов используются максимальные значения коэффициентов корреляции в соответствующем столбце. По этой редуцированной матрице рассчитываются нагрузки для первого фактора. Они определяются как отношение суммы значений корреляции по каждому столбцу к квадратному корню из суммы всех элементов матрицы:

Для определения нагрузок следующего фактора из редуцированной матрицы корреляций вычитается та часть, которая оказывается обусловленной первым фактором. Таким образом рассчитывается матрица первичных остаточных корреляций. Эта матрица подвергается несколько утомительной в "ручных" вычислениях, но на самом деле очень важной процедуре обращения алгебраических знаков остаточных корреляций. Далее происходит выделение второго фактора по тому же алгоритму. Полученные данные используются для расчета матрицы вторичных остаточных корреляций. Процедура продолжается до тех пор, пока факторные нагрузки не исчерпают корреляционной матрицы. Исчерпанность корреляционной матрицы и, соответственно, число факторов,

которые могут быть извлечены из нее, определяются с помощью специальных критериев.

Процедура центроидного метода является итерационной. Это значит, что она может повторяться многократно. Всякий раз на каждом новом шаге происходит коррекция первичной редуцированной матрицы корреляций на основе более точного расчета ее диагональных элементов. Процедура завершается, когда новое решение оказывается практически не отличимым от того решения, которое было получено на предыдущем шаге.

В настоящее время диагональный анализ и, в частности, центроидный метод используются редко, так как они в значительной степени зависят от выбора переменных в качестве значений факторов. Эти методы в первую очередь разрабатывались в расчете на вычисления вручную. По мере развития средств вычислительной техники они уступили место более сложным вычислительным алгоритмам. Тем не менее такие процедуры могут быть выполнены и с помощью современных статистических программ. В частности, возможность осуществления процедур факторного анализа в соответствии с центроидным методом предоставляет пакет Statistica.

Решения на основе главных факторов в настоящее время являются, пожалуй, наиболее распространенным вариантом декомпозиции корреляционной матрицы на искомые компоненты. Если это решение применяется к корреляционной матрице с единичными значениями корреляций по диагонали, т.е. используется полная компонентная модель, то применяется метод главных компонент. Если диагональные элементы корректируются на основе оценок общностей, используют метод общих факторов.

Процедура решений на основе главных факторов довольно сложна для вычислений вручную. Поэтому она получила широкое распространение лишь по мере развития современной вычислительной техники. В настоящее время эти процедуры включены практически во все статистические пакеты.

Основная задача процедуры главных факторов состоит в том, чтобы в ходе анализа извлечь из корреляционной матрицы максимальное количество дисперсии. Поэтому первый фактор выделяется таким образом, чтобы обеспечить максимальные значения квадратов корреляции всех переменных с извлекаемым фактором. Ведь, как мы помним, квадраты корреляций отражают процент дисперсии, связывающей одну переменную с другой. Таким образом добиваются, чтобы сумма квадратов в первом столбце факторной матрицы была максимальной.

Второй фактор выделяется таким образом, чтобы он не коррелировал с первым фактором. При этом он должен объяснять максимальное количество дисперсии, оставшейся после выделения первого фактора. Третий и последующие факторы выделяют по тому же принципу так, что в итоге постепенно процент объясненной дисперсии в корреляционной матрице уменьшается до нулевых значений настолько, насколько это оказывается возможным в принципе.

Поскольку процедура главного фактора в первую очередь бывает нацеленной на вычленение максимально возможной дисперсии корреляционной матрицы, то, как правило, оказывается, что решение, являющееся результатом применения этой процедуры, приводит к выделению меньшего числа действительно значимых факторов по сравнению с более традиционными и более простыми диагональными методами. В этом одна из причин популярности метода главных факторов.

Оборотной стороной рассматриваемого метода является тот факт, что он использует для вычисления факторной структуры все исследуемые переменные в отличие от диагональных методов, в которых для нахождения факторного решения обычно бывает достаточно двух-трех переменных. В результате диагональные методы могут дать лучшее решение в ситуации, когда экспериментатор располагает большим числом переменных, в значительной степени дублирующих друг друга. Такое, в частности, может иметь место, когда исследуются результаты ряда многомерных тестов, описывающие различные индивидуальные свойства, такие как, например, различные свойства темперамента, характера или различные виды интеллектуальных способностей, по множеству измерений. В этой ситуации применение центроидного метода может оказаться значительно более оправданным.

Конкретные алгоритмы реализации процедуры главного фактора отражают методологию, получившую название метода латентных (характеристических), или собственных векторов и латентных (характеристических) корней, или собственных значений. Суть этой методологии состоит в нахождении вектора А и скалярной величины S, для которых было бы справедливо следующее соотношение:

Величины А и 5 называют соответственно латентным (характеристическим) вектором и латентным (характеристическим) корнем корреляционной матрицы R. Если наша задача состоит в нахождении всех векторов и корней для матрицы R, то решение принимает следующий вид:

(10.7)

В уравнении (10.7) 5 представляет собой диагональную матрицу латентных корней, а матрица А содержит латентные векторы.

Необходимо также отметить, что матрица латентных векторов имеет следующее важное свойство:

Иными словами, произведение матрицы собственных векторов па ее транспонированную версию должно давать единичную матрицу.

Таким образом, уравнение (10.7) может быть переписано следующим образом:

(10.8)

Извлекая квадратные корни из всех значений S, можно разложить эту матрицу на отдельные компоненты следующим образом:

(10.9)

Подставляя разложение (10.9) в уравнение (10.8), получаем

Тогда решение уравнения (10.5) будет предполагать разложение матрицы факторных нагрузок таким образом, что

Обратим внимание: такое решение предполагает, что число выделяемых факторов должно быть равным числу исследуемых переменных, т.е. f = k.

Следует отметить несколько важных особенностей латентных корней, иначе называемых собственными значениями. Прежде всего, необходимо сказать, что этот показатель равен сумме квадратов нагрузок по главному фактору. Иначе говоря, он отражает количество дисперсий, которые описываются каждой переменной. Если анализируемая корреляционная матрица переменных содержит единичные значения по диагонали, то сумма латентных корней оказывается равной числу исследуемых переменных. Иначе он оказывается равным сумме общностей, которые используются в качестве оценок диагональных элементов матрицы. Латентные корни оказываются всегда положительными, т.е. превышают нулевые значения, только если число факторов оказывается равным числу переменных и детерминанта корреляционной матрицы не равна нулю. Если диагональные элементы матрицы корреляций отличаются от единицы, число факторов оказывается меньшим числа переменных.

Конфирматорный факторный анализ на основе максимального правдоподобия является частным случаем метода моделирования с помощью линейных структурных уравнений (Е. Л. Григоренко [6]) и несколько отличается от рассмотренных процедур тем, что в нем происходит соотнесение выделяемой факторной структуры с уже известной исследователю, а также определяется достоверность этого соответствия. Понятно, что в этом случае исследователь должен иметь некоторые представления о структуре исследуемых переменных той или иной степени детализации. Э го могут быть предположения о числе факторов, их соответствии тем или иным исследуемым переменным и факторных нагрузках для этих переменных. Такие представления могут быть заданы какими-либо теоретическими положениями, проверяемыми в эксперименте, или же получены в результате ранее осуществленного эксплораторного факторного анализа.

В качестве примера возможностей применения таких процедур можно привести экспериментальные исследования, на основе которых строятся теории личности, получившие название факторных.

Как известно, одной из первых теорий такого рода была теория, разработанная Р. Кеттелом [20]. Вспомним, что задача Кеттела состояла в том, чтобы уменьшить разнообразие личностных характеристик, отражаемых в естественном языке, до приемлемого числа факторов, которые и должны были стать способом научного описания личности. Эта задача решалась Р. Кеттелом на основе факторного анализа данных, полученных тремя различными методами. Использовались данные наблюдения, опроса и объективного тестирования. Каждый тип данных подвергался эксплораторному факторному анализу. Была выявлена устойчивая факторная структура, основа которой воспроизводилась независимо от использовавшегося метода. Позже другие исследователи, применяя методологию Р. Кеттела, пытались воспроизвести эту структуру, но, как принято считать, эти попытки оказались не слишком удачными.

Обратим внимание на то, что и Р. Кеттел и другие исследователи использовали именно эксплораторный вариант факторного анализа, и соответствие факторных структур устанавливалось преимущественно на основе субъективной интерпретации факторов, что, несомненно, расходится с базовой методологией оценки статистических гипотез, которая обычно используется в экспериментальном исследовании. Применение процедур конфирматорного факторного анализа позволило бы более точно оценить такое соответствие.

Основная идея конфирматорного анализа состоит в том, чтобы не просто выделить тот или иной набор факторов, но еще и соотнести это решение с ранее заданным. Начальным пунктом для такой процедуры выступает следующее уравнение векторной алгебры:

(10.10)

Здесь Сkk представляет собой ковариационную матрицу для k переменных; в качестве альтернативы может использоваться и корреляционная матрица – вспомним, что корреляция представляет собой не что иное, как нормированную ковариацию; Сff – ковариационная матрица для / факторов. Как правило, предполагается, что это диагональная матрица, т.е. факторы не коррелируют друг с другом. Lkf– матрица факторных нагрузок, a 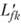– ее транспонированная версия. Ukk представляет собой диагональную матрицу ковариаций для специфических факторов, уникальных для каждой переменной. Присутствие этого параметра, очевидно, указывает на то, что процедура максимального правдоподобия базируется на модели общих факторов.

Модель, отраженная в уравнении (10.10), предполагает, что все корреляции между факторами, как общими, так и специфическими, равны нулю. Также предполагается, что сами анализируемые переменные, общие факторы и факторные нагрузки распределены в соответствии с нормальным законом. Рекомендуется проверить предположение о нормальности распределения переменных до начала факторного анализа и изъять из него те переменные, которые не удовлетворяют этому требованию в значительной степени. Также следует иметь в виду, что объем наблюдений должен быть достаточно большим – как правило, число измерений должно быть не менее 50, но достаточно достоверные результаты могут быть получены только при числе наблюдений более 200.

В результате применения процедуры максимального правдоподобия вычисляется статистика χ2. В качестве проверяемой нулевой гипотезы выступает предположение о том, что вся ковариация в генеральной совокупности описывается определенным исследователем числом факторов с заданными характеристиками. Теоретические предположения могут быть заданы факторной корреляционной матрицей Rff, матрицей факторных нагрузок или матрицей специфических факторов в уравнении (10.10). Если значение χ2 оказывается статистически значимым, скажем, на 5%-ном уровне, пулевая гипотеза отвергается и принимается гипотеза о несоответствии полученной факторной структуры теоретически предполагаемой.

Поскольку процедуры конфирматорного факторного анализа все еще не получили достаточно широкого распространения вследствие их чрезвычайной сложности и ресурсоемкости, стандартные пакеты статистического анализа, как правило, содержат только эксплораторные процедуры факторного анализа, которые не стоит путать с конфирматорными, даже если их названия оказываются сходными. Тем не менее они также в некоторых случаях дают возможность проверить простейшие гипотезы, касающиеся числа факторов. Например, в IBM SPSS Statistics для этого необходимо выбрать методы максимального правдоподобия (в русской локализации этого статистического пакета он обозначен как "максимум правдоподобия") или обобщенных наименьших квадратов (обобщенные МНК). В этом случае будут выведены значения статистики χ2, которая покажет, насколько хорошо корреляционная матрица описывается заданным числом факторов. Для получения более широких возможностей конфирматорного факторного анализа в SPSS требуется отдельный функциональный пакет моделирования структурных уравнений (SEM), который доступен в расширении AMOS (В. Byrne 1191).