Принятие решений на основе уравнений регрессии

Интерпретация моделей регрессии осуществляется методами той отрасли знаний, к которой относится исследуемое явление. Но всякая интерпретация начинается со статистической оценки уравнения регрессии в целом и оценки значимости входящих в модель факторных признаков.

Чем больше величина коэффициента регрессии, тем значительнее влияние данного признака на моделируемый.

Знаки коэффициентов регрессии говорят о характере влияния на результативный признак. Если коэффициент регрессии при факторном признаке имеет знак "+", то с увеличением значений данного фактора значения результативного признака возрастают; если коэффициент регрессии при факторном признаке имеет знак "-", то с увеличением значений данного фактора значения результативного признака уменьшаются.

Если экономическая теория подсказывает, что факторный признак должен иметь положительное значение, а коэффициент регрессии при нем имеет знак "-", то необходимо проверить расчеты параметров уравнения регрессии. Однако следует иметь в виду, что когда рассматривается совокупное влияние факторов, в силу наличия взаимосвязей между ними характер их влияния может меняться.

Частный коэффициент эластичности используют в целях расширения возможностей экономического анализа. Его определяют по формуле

где я, — коэффициент регрессии при соответствующем факторном признаке; х. — среднее значение соответствующего факторного признака; у среднее значение результативного признака.

Коэффициент эластичности показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного признака на 1%.

Рассчитаем коэффициент эластичности по исходным данным о зависимости между числом малых предприятий, их оборотом и средней численностью (см. табл. 7.6):

й, =3,041; а2 = 0,367;

Это значит, что при увеличении числа малых предприятий на 1% их оборот в среднем возрастет на 0,403%, а при повышении средней численности работников малых предприятий на 1% их оборот увеличится на 0,351%.

Частный коэффициент детерминации показывает, па сколько процентов вариация результативного признака объясняется вариацией 1-го признака, входящего в множественное уравнение регрессии:

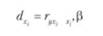
где — парный коэффициент корреляции между результативным и 1-м факторным признаком; Рг — соответствующий стандартизованный коэффициент уравнения множественной репрессии

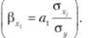
По данным, приведенным в табл. 7.6, рассчитаем частный коэффициент детерминации для фактора лг, — число малых предприятий:

Частный коэффициент детерминации для фактора х2 — средняя численность работников малых предприятий:

гп =0,757;

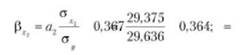
^ =0,757-0,364-0,276.

Полная экономическая интерпретация моделей регрессии позволяет выявить резервы развития и повышения деловой активности субъектов экономической деятельности.

Методы изучения связи качественных признаков

При наличии соотношения между вариацией качественных признаков говорят об их ассоциации, взаимосвязанности. Для оценки связи в этом случае используют ряд показателей.

Коэффициенты ассоциации и контингенции

Для определения тесноты связи двух качественных признаков, каждый из которых состоит только из двух групп, применяют коэффициенты ассоциации и контингенции.

Для их вычисления строят таблицу, которая показывает связь между двумя явлениями, каждое из которых должно быть альтернативным, т.е. состоящим из двух качественно отличных друг от друга значений (например, изделие годное или бракованное) (табл. 7.10).

Таблица 7.10. Таблица для вычисления коэффициентов ассоциации и контингенции

Коэффициенты вычисляют по формулам • ассоциации:

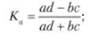
• контингенции:

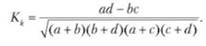
Коэффициент контингенции всегда меньше коэффициента ассоциации. Связь считается подтвержденной, если Ка >0,5 или Кь >0,3.

Пример. Исследуем связь между успеваемостью студентов и их обеспеченностью учебно-методической литературой. Результаты обследования характеризуются данными, представленными в табл. 7.11.

Таблица 7.11. Зависимость между успеваемостью студентов и их обеспеченностью учебно-методической литературой

Обеспеченность учебно-методической литературой	Численность студенток
	успевают	не успевают
Обеспечены	42	7
Не обеспечены	15	11

Рассчитаем коэффициенты:

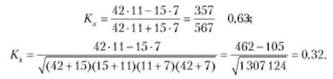
Таким образом, связь между успеваемостью студентов и обеспеченностью их учебно-методической литературой имеет место.

Коэффициенты взаимной сопряженности Пирсона и Чупрова

Если каждый из качественных признаков состоит более чем из двух групп, то для определения тесноты связи возможно применение коэффициентов взаимной сопряженности Пирсона и Чупрова. Эти коэффициенты вычисляют по следующим формулам:

где ф2 — показатель взаимной сопряженности, определяется как сумма отношений квадратов частот каждой клетки таблицы к произведению итоговых частот соответствующего столбца и строки (табл. 7.12), ф2 = у——; К. — число значений (групп) первого признака; К2 — число значений (групп) второго признака.

Чем ближе величина К{[ и Кч к единице, тем теснее связь.

Таблица 7.12. Вспомогательная таблица для расчета коэффициента взаимной сопряженности

Пример. С помощью коэффициента взаимной сопряженности исследуем связь между источниками средств на создание страховых компаний и уровнем их доходов (табл. 7.13).

Таблица 7.13. Зависимость уровня доходов страховых компаний от источников средств на их создание

Источник средств	Уровень доходов			Всего
	низкий	средний	высокий
Банковский кредит	5	7	6	18
Собственные средства	9	4	2	15
Итого	14	11	8	33

Для вычисления ф2 используется следующее выражение:

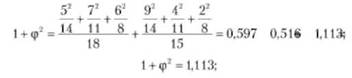
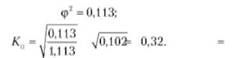
Так как К — число вариантов исследуемых признаков (три варианта признака уровня дохода и два варианта признака источника средств), получим:

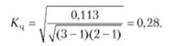
Таким образом, исследуемая между признаками связь по силе средняя.