Применение параметрической статистики при анализе эмпирических данных

Параметрическая статистика применяется в случаях, когда эмпирические показатели измерены в интервальной шкале, шкале отношений или абсолютной шкале в условиях нормального распределения экспериментальных переменных. В качестве мер центральной тенденции используются мода (Мо), медиана (Me) и среднее, или математическое ожидание (Мx). Измерение рассеяния (мер изменчивости) осуществляется посредством дисперсии (Dx) и среднеквадратического отклонения (δx), а также коэффициента вариации (V). В качестве мер связи используются коэффициенты корреляции Пирсона (Rxy) и точечно-бисериальной корреляции (Rpb)• Для статистического вывода наиболее часто используются статистические критерии и модели. К первым можно отнести /-критерий Стьюдента, υ-критерий Уэлша, F-критерий Фишера и др. Статистическое моделирование развития и изменений психологических переменных осуществляется при помощи методов линейной и нелинейной регрессии (моделей регрессии).

Таблица 1.10

Таблица результатов

№ п/п	Оценка успешности деятельности операторов	Значение коэффициента IQ операторов
1	1	1,5
2	2,5	3
3	2,5	4
4	9	8
5	10	9
6	7	7
7	5,5	6
8	4	5
9	8	10
10	5,5	1,5

Статистические методы применяются в определенном доверительном интервале, который задается исходя из потребностей точности измерений.

Доверительным интервалом называется интервал (X ± ε), который накрывает неизвестный параметр с заданной точностью. В биологических и социальных исследованиях максимальное значение ε задается в пределах 5%, т.е. ε ≤ 0,05. С понятием "доверительный интервал" тесно связан термин "уровень статистической значимости", т.е. степень воспроизводимости сходных результатов при повторном

исследовании^[1]. Значением уровня статистической значимости, часто фигурирующим в психологических публикациях, является р = 0,05. Это означает, что ошибка психологических измерений возможна в пяти случаях из 100, а статистически значимой будет информация, полученная в 95 случаях из 100.

Основной мерой центральной тенденции в параметрическом измерении является среднее значение (математическое ожидание) (Mx). Это сумма всех измеренных значений свойства, соотнесенная с количеством этих измерений.

где х. – i-e значение свойства; п – количество измерений.

Изменчивость признаков в параметрических шкалах измеряется при помощи дисперсии и среднеквадратического отклонения (δx)^[2]. Среднеквадратическое отклонение определяется как арифметическое значение квадратного корня из дисперсии, которая есть средняя арифметическая квадратов отклонений отдельных значений измеренного свойства от их среднего значения:

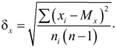
Коэффициент корреляции Пирсона (Rx ) показывает наличие статистической связи между психологическими переменными х и у, при которой каждой переменной х соответствует не одно или несколько определенных значений у, а распределение у, меняющееся вместе с изменением х, которое может быть однонаправленным (+) и разнонаправленным (-).

где хi – значение показателя первой переменной; yj – значение показателя второй переменной; N – объем выборки.

Теоретическая интерпретация коэффициента корреляции Пирсона (Rxy) подобна другим статистикам из области измерения связей между переменными. Если значение R более 0,5, то имеет место статистически сильная связь, если менее 0,5 – слабая. Положительные и отрицательные знаки показывают направленность связи (соответственно прямая и обратная).

Практическое задание. Необходимо рассчитать коэффициент корреляции Пирсона между показателями САД^[3] и IQ, измеренными в шкале интервалов (табл. 1.11).

Таблица 1.11

Таблица результатов

№ п/п	САД-оценка	IQ-баллы
1	9	115
2	8	ПО
3	8	107
4	3	93
5	2	90
6	5	100
7	6	104
8	7	105
9	4	85
10	6	115
Mx	5,8	102
δ.	2,18	9,78
As	-0,26	-0,37
Ее	1,92	1,94

Вывод: значения показателей двух тестов сильно связаны между собой. Корреляционная связь значима на уровне р < 0,05.

При определенном количестве измерений (п) корреляционные связи могут быть значимыми и незначимыми. Это необходимо знать исследователю для того, чтобы сделать достоверный вывод о причинно-следственных связях переменных. Уровень значимости коэффициентов корреляции определяется по формуле расчета t-критерия при помощи таблиц квантилей t-распределения Стьюдента для доверительной вероятности (табл. 1.12).

где R – численное значение коэффициента корреляции; п – объем выборки.

Таблица 1.12

Квантили t-распределения Стьюдента для доверительной вероятности

1-а/ 2 (а)	0,900 (α=0.2)	0,950 (α = 0,1)	0,975 (α = 0,05)	0,990 (α = 0,025)	0,995 (α = 0,01)	0,999 (α = 0,002)
f
5	1,476	2,015	2,571	3,365	4,032	5,893
10	1,372	1,812	2,228	2,764	3,169	4,144
15	1,341	1,753	2,131	2,602	2,947	3,733
18	1,330	1,734	2,101	2,552	2,878	3,610
20	1,325	1,725	2,086	2,528	2,845	3,552
23	1,319	1,714	2,069	2,500	2,807	3,485
25	1,316	1,708	2,060	2,495	2,787	3,450
26	1,315	1,706	2,056	2,479	2,779	3,435
27	1,314	1,703	2,052	2,473	2,771	3,421
28	1,313	1,701	2,048	2,467	2,763	3,408
29	1,311	1,699	2,045	2,462	2,756	3,396
30	1,310	1,697	2,042	2,457	2,750	3,385
40	1,303	1,684	2,021	2,423	2,704	3,307
60	1,296	1,671	2,000	2,390	2,660	3,232
120	1,289	1,658	1,980	2,358	2,617	3,160
∞	1,282	1,646	1,960	2,326	2,576	3,090

Здесь f – число степеней свободы, которое вычисляется для определения значимости коэффициентов корреляции f = п - 1, а для вычисления значимости различий средних двух выборок f = (n1 + п2) - 2.

Алгоритмом принятия решения по уровню значимости R может быть Вперед последовательность действий:

а) производится расчет t-критерия (по формуле);

б) по объему выборки (n -1) осуществляется вход в таблицу квантилей tp-распределения Стьюдента (См.: табл. 1.12);

в) расчетноесравнивается с ;

г) если 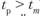, то R значим на соответствующем уровне доверительной вероятности.

Практическое задание. Рассчитаем уровень значимости коэффициентов корреляции Пирсона при их следующих значениях:

Выводом по определению уровня значимости коэффициента корреляции может являться, во-первых, утверждение о том, что он зависит от объема экспериментальной выборки и от самой величины коэффициента корреляции, и, во-вторых, даже при относительно низком коэффициенте корреляции (0,18) предпочтительнее пользоваться данными, полученными на более обширном полигоне наблюдений (1000).

Для удобства статистических расчетов и ускорения процедуры анализа данных при помощи табл. 1.13 можно получить критические значения коэффициентов корреляции.

Таблица 1.13

Критические значения коэффициентов корреляции

п/Р	0,05	0,01	N/P		0,05	0,01
4	0,950	0,990	26		0,388	0,496
5	0,878	0,959	27		0,381	0,487
6	0,811	0,917	28		0,371	0,478
7	0,754	0,874	29		0,367	0,470
8	0,707	0,834	30		0,361	0,463
9	0.666	0,798	35		0,332	0,435
10	0,632	0,765	40		0,310	0,407
11	0,602	0,735	45		0,292	0,384
12	0,576	0,708	50		0,277	0,364
13	0,553	0,684	60		0,253	0,333
14	0,532	0,661	70		0,234	0,308
15	0,514	0,641	80	0,219		0,288
16	0,497	0,623	90	0,206		0,272
17	0,482	0,606	100	0,196		0,258
18	0,468	0,590	125	0,175		0,230
19	0,456	0,575	150	0,160		0,210
20	0,444	0,561	200	0,138		0,182
21	0,433	0,549	250	0,142		0,163
22	0,423	0,537	300	0,113		0,148
23	0,413	0.526	400	0,098		0,128
24	0,404	0,515	500	0,088		0,115
25	0,396	0,505	1000	0,062		0,081

Точечно-бисериалъный коэффициент корреляции Пирсона (Rpb) – это метод корреляционного анализа отношений переменных, одна из которых измерена в дихотомической шкале наименований, а другая в интервальной шкале, шкале отношений или шкале порядка. Применяется он и для определения дискриминативности заданий методик^[4].

где – среднее по X объектов со значением с 1 по 7;

- среднее по X объектов со значением с 0 по 7; стандартное отклонение всех значений по X; – число объектов с 1 по 7; – число объектов с 0 по 7; п – общее число объектов.

Интервал измерения от -1 до +1. Теоретическая интерпретация значений подобна .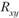

Практическое задание. Предлагается рассчитать величину статистической взаимозависимости показателей теста САД по направленности на техническую деятельность и уровня обучаемости испытуемого (в сырых оценках) (табл. 1.14).

Таблица 1.14

Результаты обследования

Номер испытуемого	Техническая направленность	Оценка обучаемости	Расчет Rpb
1	1	16
2	0	8
3	1	14
4	1	18
5	1	И
6	1	15
7	0	9
8	0	5
9	0	9
10	0	4

Расчет коэффициентов корреляции служит инструментом, позволяющим осуществить корреляционный, факторный и кластерный анализ эмпирических данных. В основу факторного и кластерного анализа положено представление о корреляционных зависимостях, т.е. процедура корреляционного анализа.

Корреляционный анализ (correlatio от лат. – соотношение, связь, зависимость) – это комплексный метод исследования взаимозависимости признаков в генеральной совокупности, являющихся случайными величинами и статистически связанными. Корреляционный анализ, как правило, осуществляется с психологическими переменными, имеющими нормальное многомерное распределение. Процедуры корреляционного анализа позволяют определить степень значимости связи, установить силу и направление влияния системы переменных (X) на зависимую переменную, а также корреляционную структуру как зависимой, так и независимой переменных в ходе психологического исследования.

Для наглядности система корреляционных зависимостей представляется в виде таблиц корреляций переменных, матриц и графов (табл. 1.15 и 1.16).

Таблица 1.15

Треугольная корреляционная матрица

Признаки	1-й	2-й	3-й	4-й	5-й	6-й
1-й	1	0,59	0,3	0,44	0,16	0,41
2-й		1	0,42	0,57	0,66	0,51
3-й			1	0,38	0,39	0,41
4-й				1	0,62	0,59
5-й					1	0,55
6-й						1

Таблица 1.16

Четырехугольная корреляционная матрица

Признаки	1-й	2-й	3-й	4-й	5-й	6-й
1-й	1	0,59	0,3	0,44	0,16	0,41
2-й	0,59	1	0,42	0,57	0,66	0,51
3-й	0,3	0,42	1	0,38	0,39	0,41
4-й	0,44	0,57	0,38	1	0,62	0,59
5-й	0,16	0,66	0,39	0,62	1	0,55
6-й	0,41	0,51	0,41	0,59	0,55	1

Факторный анализ – раздел многомерного статистического анализа, сущность которого заключается в выявлении непосредственно не измеряемого (скрытого) признака, являющегося главной компонентой (производной) группы измеренных тестовых показателей. Создатель факторного анализа Ч. Спирмен выявил латентную составляющую интеллекта (1904), что положило начало бесконечным пробам факторизации психологических переменных. Центральной задачей данного метода является переход от совокупности непосредственно измеряемых признаков к системообразующим факторам, за которыми стоят реальные эмпирические данные, отражающие реальные психологические структуры. Сам фактор есть отражение реальности. Он призван, по меткому выражению Л. Терстоуна, "конденсировать" результаты психологических измерений, упрощать, сокращать (редуцировать) их и превращать материю цифр в "дух" психологической науки. Это поистине "самый психологический из всех статистических методов".

Наглядно фактор может быть представлен в виде модели "прошивания" измеренных переменных с целью выявления общего существенного элемента, отражающего главную особенность этих частных переменных (рис. 1.10).

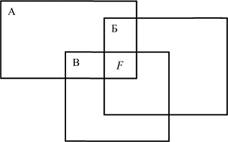
Рис. 1.10. Модель факторного анализа

Данные корреляционного и факторного анализа помогают обнаружить взаимосвязи между переменными, но, как полагают некоторые исследователи, не могут стать достаточным основанием для выводов о причинно- следственных зависимостях и об иерархии причинных связей. Выделение факторов более высокого порядка и другие модификации сути метода не меняют. Какую бы понятийную систему психолог ни использовал, в ней непременно заложен принцип причинности, который пронизывает любую концепцию. В этом существенное расхождение понятийного и факторного подходов к описанию психических явлений. Никакая формализованная процедура не может заменить концептуальные представления и логику исследователя. В факторном анализе предполагается, что наблюдаемые переменные являются математической комбинацией некоторых латентных (гипотетических или ненаблюдаемых) факторов. Однако опыт и наличие дополнительной информации о структуре исследуемого явления позволяют достаточно корректно интерпретировать результаты факторного анализа.

В психологии факторный анализ используется довольно широко и зачастую механически, без учета его возможностей. Схемы факторного анализа мозаичны. По свидетельству Б. В. Кулагина (1984), у исследователей пока "нет общепринятой процедуры факторного анализа, имеются существенные несовпадения во взглядах на приемлемость и обоснованность различных алгоритмов и подходов"^[5].

Л. В. Куликов (1994) рекомендует соблюдать ряд основных требований для корректного применения факторного анализа. Во-первых, переменные должны быть измерены на уровне ординальной шкалы или шкалы интервалов (но классификации С. Стивенса). Во-вторых, отбирая переменные для факторного анализа, следует учитывать, что на один фактор должно приходиться по крайней мере три переменных. В-третьих, для обоснованного решения необходимо, чтобы число экспериментальных переменных не превышало одной трети от числа испытуемых. Следует всегда отдавать себе отчет, что исследовательская практика постоянно вносит коррективы, и поэтому психологу следует исходить из того, что чем сильнее нарушается это правило, тем менее точными будут результаты.

В-четвертых, нецелесообразно включать в факторный анализ переменные, у которых очень слабы связи с остальными переменными, потому что они будут иметь малую общность и не войдут ни в один фактор.

В-пятых, важнейшим моментом поиска хорошего факторного решения является определение числа факторов перед их "вращением". В окончательном решении лучше всего основываться на содержательных предположениях о структуре изучаемого явления.

При выборе переменных и сокращении их количества для следующего цикла факторного анализа можно использовать переменные, если отбирать их по факторным общностям. При интерпретации факторов можно начать работу с того, что выделить наибольшие факторные нагрузки в данном факторе. Для выделения можно использовать приемы, аналогичные выделению значимых коэффициентов корреляции, множественной детерминации () (Uberia К., 1980), а также расчеты интенсивности и экспансивности факторов^[6].

На практике исследователь путем выявления статистически значимых корреляционных плеяд строит фактор, назовем ero X. В табл. 1.15 и 1.16 приведены данные корреляционного анализа, из которых видно, что переменные 2, 4, 5 и 6 связаны между собой статистически сильной связью и образуют общий признак (рис. 1.11).

Рис. 1.11. Графический вид гипотетического фактора X

Наибольшей интенсивностью обладает пятая переменная. Она же может взять на себя роль системообразующей. Если, например, эти переменные в ходе эксперимента обозначают какие-либо психические свойства личности, то их совокупность является обобщенным качеством или психологическим фактором, где пятая переменная играет ведущую роль. Математический фактор становится психологическим не сам по себе, а в ситуации его стабильной связи с практическим проявлением изучаемого свойства Y (рис. 1.12).

Рис. 1.12. Графический вид гипотетического фактора X во взаимосвязи с Y

Кластерный анализ представляет собой совокупность статистических и иных, в том числе качественных, методов, предназначенных для дифференциации относительно отдаленных друг от друга групп и близких между собой объектов по информации о связях или мерах близости между ними.

В ходе исследования проявлений типовых признаков часто пользуются процедурой кластерного анализа. Типология определяется путем выявления признаков, близких к эталону по их дисперсии. В этом случае корреляция осуществляется не между переменными, а между субъектами, носителями признаков. Эта близость определяется по наименьшей дисперсии реальных носителей признаков относительно признаков эталона. В табл. 1.17 приведены экспериментальные данные, полученные в ходе психологического исследования. Объем экспериментальной выборки – четыре человека. Измерено пять психологических переменных.

Таблица 1.17

Экспериментальные данные, полученные в ходе психологического исследования

Носители признаков	Признак 1	Признак 2	Признак 3	Признак 4	Признак 5
Субъект 1	3	10	8	3	2
Субъект 2	4	8	7	4	4
Субъект 3	9	2	4	1	8
Субъект 4	10	3	5	1	9

Допустим, что дисперсионный и корреляционный анализ выявил, что субъекты 1 и 2, как и субъекты 3 и 4, могут быть объединены в две группы, или два разных кластера. Наглядно это представлено на рис. 1.13.

Рис. 1.13. Проявление психологических признаков у испытуемых

Статистические критерии (Хи-квадрат Пирсона, ί-критерий Стьюдента, v-критерий Уэлша, F-критерий Фишера и др.) представляют собой методы статистического вывода о наличии значимой связи между признаками или выявления признака, характеризующего генеральную совокупность. Критерий Хи-квадрат Пирсона – непараметричсский критерий. Статистические критерии Стьюдента, Уэлша и Фишера – критерии параметрические. На практике они применяются для оценки подобия двух групп испытуемых, у которых измерены определенные свойства, по средней и дисперсии эмпирических данных. ί-Критерий в отличие от v-критерия применяется в ситуации равенства среднеквадратических отклонений переменных. F-критерий определяет подобие выборок по дисперсии их эмпирических переменных. Формулы расчета эмпирических значений статистических критериев приведены ниже.

где Мх. – средние значения тестовых данных; п – количество испытуемых; δ – среднеквадратическое отклонение.

где φ1 – угол, соответствующий большей процентной доле; φ2 – угол, соответствующий меньшей процентной доле; п1 – количество наблюдений в первой выборке; п2 – количество наблюдений во второй выборке.

Анализ результатов исследования при помощи, например, ί-критерия Стьюдента осуществляется по следующему алгоритму: а) производится расчет значений ί-критерия;

б) по количеству испытуемых осуществляется вход в таблицу квантилей ί-распределения Стьюдента (См.: табл. 1.12);

в) значение расчетного ί-критерия (tρ) сравнивается с табличным значением (tт); г) если tρ > tт, то выборки значимо различаются на уровне доверительной вероятности; д) если t < f, то группы испытуемых принадлежат одной совокупности.

Практическое задание. Требуется определить однородность выборок по средним значениям уровня интеллекта, измеренного при помощи методики САД, т.е. ответить на вопрос: "Какие контрольные группы вместе с экспериментальной принадлежат одной совокупности?".

Показатели тестирования экспериментальной группы и трех контрольных выборок помещены в табл. 1.18. Расчет необходимо произвести с использованием параметрического статистического критерия, так как эмпирические данные представлены па интервальном уровне. ί-Критерий Стьюдента является параметрическим критерием.

Таблица 1.18

Тестовые (сырые) показатели методики САД

№ п/п	САД-экси.	САД-1	САД-2	САД-3
1	9	1	5	8
2	8	2	7	9
3	8	1	6	8
4	3	3	4	4
5	2	1	1	3
6	5	3	5	5
7	6	3	7	6
8	7	4	7	7
9	4	2	2	4
10	6	5	3	6
Mx	5,8	2,5	4,7	6
δx	2,18	1,28	2,05	1,9

Расчетный ί-критерий по данным экспериментальной и первой выборок равен 3,91 (р < 0,001)^[7], ί-критерий по данным экспериментальной и второй выборок равен 1,1 (р< 0,3); ί-критерий но данным экспериментальной и третьей выборок равен 0,21 (р < 0,8). Так, составляет 2,01.

Вывод, следующий из решения примера, таков: экспериментальная группа и первая выборка значимо различаются. Вторая и третья выборки с экспериментальной группой составляют одну совокупность, т.е. однородны или эквивалентны.