Лекция 11. ПРИМЕНЕНИЕ МАТЕМАТИЧЕСКИХ МЕТОДОВ В ЭКОНОМИЧЕСКОЙ ГЕОГРАФИИ

После изучения главы 11 студенты должны:

знать

• сущность и направления математико-географического моделирования;

• модели региональной и национальной экономики;

• основные виды прогнозов в экономической географии;

уметь

• разрабатывать основные виды моделей, используемых в экономико-географическом анализе;

• анализировать проблемы размещения и развития производительных сил на основе математико-географических моделей;

владеть

• методами сбора, обработки, анализа и интерпретации экономикогеографической информации для разработки математико-географических моделей;

• навыками анализа и прогнозирования экономико-географических процессов.

Сущность и направления математико-географического моделирования

Особое значение для развития методологии экономико-географических исследований имеет моделирование. Активное проникновение в географию системного подхода, конкретизация методов исследований, необходимость в четкой формулировке задач и их строгого решения привели к развитию математических методов в географии^[1].

Предварительно сделаем одно принципиальное замечание, касающееся различий в понятиях "метод" и "модель".

Метод, как отмечалось выше, – это способ познания, исследования явлений природы и общественной жизни. Модель (от лат. "modulus" – мера, образец) – это схема, изображение или описание какого-либо явления или процесса в природе и обществе. Принимая во внимание обе дефиниции, можно утверждать, что модель есть составная часть метода. В связи с этим в ходе объяснения сущности того или иного метода могут появляться модельные термины.

Термин "модель" широко распространен как в научном, так и в общеупотребительном языке, причем в разных ситуациях в него вкладывается различный смысл. В самой общей формулировке модель – это условный образ объекта исследования, сконструированный для упрощения данного исследования.

Моделируя геосистему или какие-то ее элементы (например, структуру либо процесс функционирования), мы создаем искусственно ее аналог (копию) в упрощенном виде. Имитировать сложную систему во всем ее многообразии практически невозможно. Важно, чтобы модель описывала главные свойства объекта, воспроизводила отношения между его элементами, виды и характер внутрисистемных и внешних связей, причем в тех или иных количественных показателях. В связи с этим моделирование содержит не только качественные, но и количественные критерии для анализа исследуемого объекта. Это дает возможность совершенствовать моделируемый объект и на этой основе вырабатывать стратегию регулирования развития самой геосистемы.

Математико-географическое моделирование представляет собой сложный процесс, состоящий из ряда последовательных этапов.

1. Подготовительный этап, в ходе которого ставят цель и определяют задачи исследования. На основе предварительных данных о системе выявляют потребность в применении метода математического моделирования. Затем в соответствии с целями исследования формулируют задачи моделирования относительно данной системы.

2. Второй этап состоит из ряда последовательных операций:

– выявления характера взаимосвязанности сформулированных на подготовительном этапе задач;

– установления последовательности решения этих задач.

3. Третий этап – построение моделей для решения каждой из поставленных задач.

Примерами моделей в географии могут служить следующие.

1. Модели класса географических задач выявления связей между элементами системы: оценка баланса энергии и биомассы Земли, задачи измерения перемещения отдельных точек земной поверхности, характеристика развития отдельных эрозионных форм в бассейнах рек, изучение связей в ландшафтах, оценка природных режимов географической среды, количественная оценка связей радиационного баланса в различных географических фациях, оценка интенсивности развития овражной эрозии, выявление ведущих факторов сложных связей в системе, оценка связи между численностью населения города с уровнем его развития, определение структуры территориально-производственного комплекса и др.

2. Модели класса задач анализа элементов системы: статистический анализ границ лавиноопасных зон, нахождение основ проектирования полезащитных лесных полос, морфометрический анализ при проектировании различных инженерных сооружений, определение плотности населения города и др.

3. Модели класса задач районирования (и зонирования): выделение типов природных ландшафтов в зависимости от радиационного индекса сухости, распознавание образцов для выделения районов и анализ таксономического расстояния в я-мерном пространстве, выявление зон влияния городов, районирование территорий и др.

Одной из первых макроэкономических моделей была модель воспроизводства Ф. Кене (1758). Современное развитие моделирования экономических процессов связано с комплексом экономико-математических методов и эконометрикой^[2]. Эконометрические модели разрабатываются для прогнозирования таких экономических показателей, как ВНП, личный доход, расходы на личное потребление, капиталовложения, правительственные закупки товаров и услуг, чистый экспорт и т.д.

Исследование зависимостей и взаимосвязей между объективно существующими явлениями и процессами играет большую роль в экономике. Метод изучения связей в статистике называют регрессионным анализом, а связи – регрессионными.

Математически задача формулируется следующим образом.

Требуется найти аналитическое выражение зависимости экономического явления (например, производительности труда) от определяющих его факторов; т.е. ищется функция у = f (.х1, х2, ..., хn), отражающая в среднем зависимость, по которой, зная значения независимых факторов xi, можно найти приближенное значение зависимого от них показателя у.

Для нахождения уравнения регрессии необходимо определить общий вид функциональной зависимости и рассчитать параметры уравнения (часто используется метод наименьших квадратов). При выборе вида зависимости руководствуются следующим: он должен согласовываться с профессионально-логическими соображениями относительно природы и характера исследуемых связей; по возможности используют простые зависимости, не требующие сложных расчетов, легко поддающиеся интерпретации и практическому применению. Технология разработки регрессионной модели описана практически в каждом учебнике по общей теории статистики и эконометрике.

Регрессионные модели социально-экономических объектов и процессов используют во многих областях в зависимости от вида применяемых функций.

Парная линейная регрессия используется при изучении функции потребления:

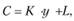
где С – потребление; у – доход; К и L – параметры функции.

Среди класса нелинейных функций следует назвать равностороннюю гиперболу

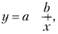
которая используется для характеристики многих видов связей. Например, для характеристики связи удельных расходов сырья, материалов, топлива с объемом выпускаемой продукции, времени обращения товаров от величины товарооборота как на микро-, так и на макроуровне.

Классическим ее примером является кривая Филипса, характеризующая нелинейное соотношение между нормой безработицы x и процентом прироста заработной платы у:

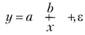
где ε – случайное отклонение.

Это уравнение, отражающее обратную зависимость указанных показателей, было получено в конце 1950-х гг. английским экономистом А. В. Филипсом на основе данных, обобщенных более чем за 100-летний период.

Аналогичным примером может служить также взаимосвязь доли расходов на товары длительного пользования и общих сумм расходов (или доходов). Математическое описание подобного рода взаимосвязей получило название кривых Энгеля. В 1857 г. немецкий статистик Э. Энгель на основе исследования семейных расходов сформулировал следующую закономерность: с ростом дохода доля расходов па продовольствие уменьшается. Следовательно, с увеличением дохода доля их расходов на непродовольственные товары будет возрастать.

В исследованиях урожайности, трудоемкости сельскохозяйственного производства используются уравнения с квадратными корнями, комбинации тригонометрических функций.

Множественная регрессия применяется в решении проблем спроса, доходности акций, при изучении функции издержек производства, в макроэкономических расчетах и т.д.

В 1930-е гг. Дж. М. Кейнс сформулировал гипотезу потребительской функции. Впоследствии исследователи неоднократно обращались к проблеме ее совершенствования. Современная потребительская функция рассматривается как модель следующего вида:

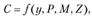
где С – потребление; у – доход: Р – цена стоимости жизни; М – наличные деньги; Z – ликвидные активы.

Особую роль в моделировании социально-экономических систем играют производственные функции, которые связывают значения вектора продукции у со значениями вектора ресурсов x:

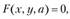
где а = а1, ..., аn – вектор параметров производственной функции.

Вместо общего представления производственной функции часто используют два частных случая.

1. Функции выпуска, в которых в качестве независимых переменных берутся затраты ресурсов, а функцией является выпуск: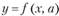

2. Функции производственных затрат, в которых независимой переменной является выпуск, а функцией – затраты: .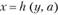

Подробное описание использования производственных функций в моделировании дано в параграфе 11.3, где рассматриваются модели региональной и национальной экономики, так как именно на этих уровнях хозяйственной иерархии они находят наибольшее применение.

В некоторых случаях исследуется зависимость изучаемого явления или объекта от времени, т.е. моделируется его динамика (см. параграф 11.2).