Прикрепление потребителей к поставщикам методами линейного программирования

Прикрепление потребителей к поставщикам может выполняться различными методами в зависимости от характера и размера решаемой задачи. Разработанные в последнее время математические методы планирования, применение ЭВМ для прикрепления потребителей к поставщикам создали возможности для составления оптимальных планов перевозок грузов, ликвидации многих нерациональных перевозок.

В последние годы в теории оптимального программирования (линейное, динамическое и стохастическое) разработаны математические методы (алгоритмы) для решения транспортных задач, позволяющие путем ряда последовательных расчетов найти оптимальный вариант.

Среди математических методов наиболее разработаны методы линейного программирования. Слово "линейное" определяет математическую сущность метода, который заключается в том, что с сто помощью решают задачи с линейными связями и ограничениями, т.е. если выразить задачу в математической форме, то в ней все неизвестные будут в первой степени. Слово "программирование" показывает, что математические методы применяют для планирования, составления программы (плана).

Оптимальное прикрепление потребителей к поставщикам с применением методов линейного программирования снабженческо-сбытовые органы осуществляют в виде транспортной задачи. Для составления экономико-математической модели необходимо знать следующие данные: потребность потребителей, ресурсы поставщиков, транспортные расходы на перевозку продукции и некоторые другие. Затем надо сформулировать задачу и составить экономикоматематическую модель.

Постановка задачи

Пусть имеются т поставщиков, располагающих определенным количеством продукции, и п потребителей, которым выделены фонды на данную продукцию. Известны транспортные расходы по доставке единицы продукции от любого поставщика до любого потребителя. Требуется прикрепить потребителей к поставщикам так, чтобы суммарные транспортные расходы по доставке всей продукции потребителям были минимальные.

Для построения экономико-математической модели вводятся обозначения:

i – номер (индекс) поставщика (i = 1, 2, ..., т) пусть т = 4, т.е. имеются четыре поставщика (i = 1, 2, 3, 4);

Ai – ресурсы i-го поставщика (i = 1, 2, 3, 4), т.е. количество продукции, которое поставщик может отправить потребителям: A1 = 160 т; A2 = 240 т; А3 = 100 т; A4 = 200 т; всего – 700 т;

j – номер (индекс) потребителя (j = 1, 2, п); пусть п = 5, тогда; j = 1, 2, 3, 4, 5;

В, – фонд (потребность) j-го потребителя: B1 = 150 т; В2 = 180 т; В3 = 200 т; В4 = 120 т; В5 = 50 т; всего – 700 т;

Сij – транспортные расходы по доставке единицы от i-го поставщика j-му потребителю; эти расходы приведены в табл. 5.4.

Таблица 5.4

Транспортные расходы по доставке единицы продукции i-го поставщика j-му потребителю

Поставщики	Потребители
	j = 1	j = 2	j = 3	j = 4	j = 5
i = 1	С11= 2	С12= 6	С13= 4	С14= 10	С15= 4
i = 2	С21 = 7	С22= 5	С23= 2	С24= 7	С25= 10
i = 3	С31 = 5	С32= 2	С33= 6	С34= 5	С35= = 9
i = 4	C41 = 3	С42= 9	С43= 4	С44= 4	С45= 4

Xij – количество продукции, поставляемой от i-го поставщика j-му потребителю; эта величина подлежит определению (табл. 5.5).

Таблица 5.5

Количество продукции, поставляемое от i-го поставщика j-му потребителю

Поставщики	Потребители
	j = 1	j = 2	j = 3	j = 4	j = 5
i = 1	X11 (Xij)	X12 …	X13 …	X14 …	X15 …
i = 2	X21 (Xij)	X22 …	X23 …	X24 …	X25 …
i = 3	X31 (Xij)	X32 …	X33 …	X34 …	X35 …
i = 4	X41 (Xij)	X42 …	X43 …	X44 …	X45 …

После введения обозначений и принятия числовых значений (ресурсы поставщиков, потребность потребителей и транспортных расходов по доставке продукции) составим табл. 5.6. Укажем в ней исходные данные для решения экономико-математической модели, ресурсы поставщиков, потребности потребителей и транспортные расходы (они проставлены в выделенных прямоугольниках). Кроме того, в табл. 5.6 предусмотрен столбец для записи потенциалов Ui и Vj.

Приступим к построению модели. Экономико-математическая модель оптимального прикрепления содержит целевую функцию, системы ограничений (определенные условия) и условия неотрицательности переменных.

Таблица 5.6

Исходные данные для оптимального решения прикрепления потребителей к поставщикам

Поставщики		Потребители										Ресурсы поставщиков
		j = 1		j = 2		j = 3		j = 4		j = 5
	Vj / Ui	V1		V2		V3		V4		V5
i = 1	U1		2		6		4		10		4	160
		X11		X12		X13		X14		X15
i = 2	U2		7		5		2		7		10	240
		X21		X22		X23		X24		X25
i = 3	U3		5		2		6		5		9	100
		X31		X32		X33		X34		X35
i = 4	U4		3		9		4		4		4	200
		X41		X42		X43		X44		X45
Потребители		150		180		200		120		50		700

В рассматриваемой модели ставится задача свести к минимуму транспортные расходы.

Для нашего числового примера (см. табл. 5.6) целевая функция будет иметь вид

В общем виде целевая функция выглядит так:

или

Достижение минимального значения целевой функции должно происходить при определенных условиях. Первое из них состоит в том, что по оптимальному варианту от каждого поставщика планировалось к поставке то количество продукции, которым он располагает. Это условие для рассматриваемого примера записывается в виде системы уравнений.

В общем виде система уравнений для первого условия записывается так:

(5.1)

или

Для числового примера (см. табл. 5.5):

(5.2)

Второе условие предусматривает поставку каждому потребителю продукции в пределах потребности.

В общем виде система уравнений для второго условия записывается в виде

(5.3)

или

Для числового примера (см. табл. 5.5):

(5.4)

Наконец, в модели указывается присущее многим моделям условие неотрицательности переменных, т.е. значение переменной (поставки) должно быть равно нулю или больше нуля (отрицательное значение поставки не имеет смысла, например, минус 20 т металла):

(5.5)

Таким образом, экономико-математическая модель оптимального прикрепления потребителей к поставщикам будет иметь следующий вид:

(5.6)

при условиях:

(5.7)

; (5.8)

(5.9)

Приведенная модель соответствует закрытой модели, так как . Если же условия равенства ресурсов и потребности нет, то строится открытая модель.

После построения экономико-математической модели решается задача прикрепления поставщиков к потребителям. Расчеты выполняют в специальной таблице (матрице) линейного программирования методом потенциалов (табл. 5.7). В таблице, кроме ресурсов поставщиков, потребителей и транспортных расходов, имеются столбец и строка для записи потенциалов Ui и VJ, которые дают возможность определить оптимальность плана закрепления поставщиков за потребителями.

Таблица 5.7

Исходный оптимальный план прикрепления потребителей к поставщикам (матрица)

Поставщики, m		Потребители, п										Ресурсы поставщиков
		j = 1		j = 2		j = 3		j = 4		j = 5
	Vj / Ui	V1 = 2		V2 = 6		V3 = 3		V4 = 3		V5 = 3
i = 1	U1 = 0		2		6		4		10		4	160
		150		100		3		3		3
i = 2	U2 = –1		7		5		2		7		10	240
		1		170		70		2		2
i = 3	U3 = 3		5		2		6		5		9	100
		5		9		100		6		6
i = 4	U4 = 1		3		9		4		4		4	200
		3		7		30		120		50
Потребители		150		180		200		120		50		700

Решение задачи начинается с построения исходного плана. Метод потенциалов, как и другие методы линейного программирования, требует, чтобы исходный вариант и все последующие варианты удовлетворяли условиям:

1) число загруженных клеток Хij в таблице должно быть на единицу меньше суммы чисел поставщиков (т) и числа потребителей (n). В нашем примере это число должно быть равно 8, т.е. т + п – 1 = 44 – 5 – 1 = 8;

2) не должно быть ни одного занятого квадрата, который оказался бы единственным в строке и в столбце таблицы;

3) занятые квадраты таблицы должны быть расположены так, чтобы можно было образовать так называемую вычеркиваемую систему.

Для составления исходного плана воспользуемся приемом, который называется методом северо-западного угла. Согласно этому методу заполнение таблицы прикрепления следует начать с левого верхнего квадрата и с позиции этого квадрата сравнить ресурсы первого поставщика (160 т) и потребности первого потребителя (150 т), выбрать меньшее значение из них и записать в данный квадрат, который с этого момента становится загруженным.

В нашем примере записано значение "150", равное потребности первого потребителя. Затем необходимо подвинуться вправо от северо-западного угла и сравнить оставшиеся ресурсы первого поставщика 10 (160 – 150 = 10) и потребность второго потребителя (180); записываем наименьшую цифру (10) в квадрат первой строки второго столбца и перемещаемся вниз. Сравниваем неудовлетворенную потребность второго потребителя 170 (180 – 100). Ресурсы второго поставщика составляют (170 + 70 = 240) и т.д.

Так, двигаясь шаг за шагом, получаем исходный план. Определим значение некоторых цифр, содержащихся в табл. 5.7. Числа, выделенные в таблице, – это количество продукции, которое по исходному плану намечено к поставке. Квадраты, в которых расположены эти цифры, называются загруженными, квадраты, не содержащие поставок, – свободными.

Числа, расположенные в свободных квадратах табл. 5.7, являются вспомогательными и представляют собой сумму соответствующих условных величин Ui + Vj = `Сij (потенциалов). Для "загруженных" квадратов суммы Ui + Vj должны совпадать с транспортными издержками Сij.

После составления исходного плана проверим условие т + п – 1 = 8, т.е. необходимо иметь 8 загруженных клеток, что мы и имеем.

По исходному варианту транспортные расходы, руб., составят:

Вперед стадия заключается в проверке исходного плана на оптимальность. Для этого необходимо определить индексы . Индексы определяются для загруженных клеток. Сумма индексов должна быть равна транспортным издержкам Q, т.е. и т.д. В нашем примере значения Ui и Vj должны быть такими, чтобы

Индексы определяем следующим образом.

Принимаем U2 = 0, тогда Y, = 2, так как то

Аналогично определяем значение V2. Так как , то

так как

Далее определяем индекс U2. Так как а то

Теперь можно определить индекс Vs. Исходя из того что , его значение

Продвигаясь подобным образом последовательно по всем загруженным квадратам, нетрудно определить все значения Ui и Vj

Далее исчисляем значения и записываем в "свободные"

квадраты. Например, и т.д.

Записанные значения сумм Ui + Vj в свободных квадратах , как правило, отличаются от значений Cif (транспортные издержки).

При этом возможны три случая:

1) ;

2) ;

3)

Сравниваем и определяем, является ли полученный вариант прикрепления потребителей к поставщикам оптимальным.

Если для всех свободных квадратов оказывается, что , то план считается оптимальным. Если хотя бы в одном из квадратов это условие не соблюдено, считается, что план не является оптимальным и его можно улучшить. В нашем примере (см. табл. 5.7) план не является оптимальным, так как Следовательно, его можно улучшить.

Улучшают вариант путем перемещения поставки в "свободные" квадраты, для которых . Если имеется несколько свободных квадратов, необходимо осуществлять перемещение для той, у которой . В нашем примере этот квадрат расположен в третьей строке второго столбца ().

В другом квадрате эта разность меньше ().

В случае, если разность окажется одинакова для сравниваемых свободных квадратов, следует выбирать один из них произвольно.

Итак, в рассматриваемом примере поставка должна быть перемещена в квадрат третьей строки и второго столбца. Перемещения производятся в определенном порядке с тем, чтобы не были нарушены условия, выраженные в приведенных выше уравнениях. Для этого образуем связку, т.е. замкнутую ломаную линию, состоящую из горизонтальных и вертикальных отрезков, таким образом, чтобы одной из вершин образованного многоугольника был сам свободный квадрат, а остальные вершины находились в занятых квадратах.

Свободный квадрат может быть соединен четырьмя прямыми отрезками с соседними занятыми квадратами, как это показано ниже (рис. 5.3).

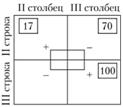
Рис. 5.3. Образование свободного квадрата

После образования связки свободному квадрату и связанным с ним загруженным квадратам присваиваем поочередно знаки "–" или "+", начиная со свободного квадрата. В приведенной табл. 5.7 показана расстановка знаков. Направление расстановки знаков безразлично.

Далее просматриваем те запятые квадраты, которым присвоим знак "+", и выбираем тот из них, в котором содержится наименьшая поставка; в рассматриваемом примере она равна 100 т. Именно это значение подлежит перемещению из каждого квадрата со знаком "+" в каждый квадрат (в том числе и свободный) со знаком "-". Перемещение выглядит так:

В результате перемещения получаем новый вариант прикрепления (табл. 5.8). Транспортные расходы составляют 2050 руб., т.е. они на 700 руб. меньше, чем в исходном варианте. Расчеты показали, что план оптимальный. Отсутствуют потенциальные клетки.

Таблица 5.8

Исходный оптимальный план прикрепления потребителей к поставщикам (новый вариант прикрепления)

Поставщики, m		Потребители, п										Ресурсы поставщиков
		j = 1		j = 2		j = 3		j = 4		j = 5
	Vj / Ui	V1 = 2		V2 = 6		V3 = 3		V4 = 3		V5 = 3
i = 1	U1 = 0		2		6		4		10		4	160
		150		100		3		3		3
i = 2	U2 = –1		7		5		2		7		10	240
		1		170		70		2		2
i = 3	U3 = 3		5		2		6		5		9	100
		5		9		100		6		6
i = 4	U4 = 1		3		9		4		4		4	200
		3		7		30		120		50
Потребители		150		180		200		120		50		700