Правило простого большинства

На практике наиболее распространенная процедура принятия коллективных решений предполагает применение правила простого большинства. Согласно этому правилу побеждает альтернатива, в поддержку которой высказываются более половины участников выбора (голосования). Закономерен вопрос: почему при решении самых разных проблем в весьма непохожих друг на друга сообществах используется одна и та же процедура? Естественно ожидать, что ей присуще какое-то свойство, снижающее, при прочих равных условиях, сумму внутренних и внешних издержек коллективного выбора.

Если для принятия решения достаточно менее половины или ровно половина голосов, то всегда есть вероятность одновременного голосования за два взаимоисключающих варианта. Так, при четном числе голосующих возможно, что половина участников выбора одобрит один вариант бюджета, а вторая половина – другой. Если для принятия решения простого большинства не требуется, то окажется, что оба варианта подлежат реализации. На практике подобная тупиковая ситуация, по-видимому, предполагала бы проведение переговоров между голосующими, с тем чтобы наметить компромиссный вариант. Однако, будучи вынесенным на голосование, он также мог бы получить одобрение наряду с другим, отличающимся от него. Понятно, что если решение считается принятым при подаче менее чем половины голосов, вероятность многократного повторного (если не бесконечного) обсуждения еще выше.

Таким образом, есть основания полагать, что при переходе от правила, согласно которому решение принимается N/2 голосами (N – число голосующих), к правилу, требующему одобрения (N/2 + 1) голосами (к правилу простого большинства), происходит скачкообразное уменьшение внутренних издержек D. При прочих равных условиях, такое уменьшение влечет за собой резкое снижение суммарных издержек (D + E). Описанное достоинство правила простого большинства тем существеннее, чем более значимы внутренние издержки, т.е. чем выше члены голосующего сообщества оценивают затраты времени и усилий на достижение согласия.

Итак, требование простого большинства – минимальное требование к решающей подгруппе, при котором предотвращается принятие взаимоисключающих решений.

Естественно ожидать, чтобы применяемые на практике процедуры принятия решений отвечали определенным нормативным требованиям, согласующимся со здравым смыслом. В данном параграфе мы убедимся, что по отношению к некоторому набору таких требований правило простого большинства отличается уникальными достоинствами.

Введем следующие определения и обозначения. Строгое предпочтение альтернативы х альтернативе у имеет место в тех и только тех случаях, когда субъект выбора оценивает первую возможность выше второй. Соответствующее строгое предпочтение i-го индивида записывается , а аналогичный результат коллективного выбора – . Нестрогое предпочтение альтернативы х альтернативе у означает, что, с точки зрения делающего выбор субъекта, первая альтернатива лучше или равноценна второй. Нестрогие индивидуальное и коллективное предпочтения обозначаются и . Равноценность двух альтернатив для i-го индивида записывается , а соответствующий результат коллективного выбора – .

Пусть 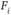– индивидуальная функция решения, которая определяется следующим образом:

, когда , когда,

, когда

– групповая функция решения, значения которой зависят от результатов коллективного выбора в группе, состоящей из п членов. Если применяется правило простого большинства, то:

F= 1, когда

F = 0, когда,

F = -1, когда

Американский исследователь Кеннет Мэй^[1] доказал, что применение правила простого большинства – единственная процедура коллективного выбора, удовлетворяющая четырем условиям, названным им соответственно достижимостью результата, анонимностью, нейтралъностъю и позитивным откликом. Эти условия (аксиомы) предполагают, соответственно, что:

1) групповая функция решения принимает одно и только одно значение для каждой пары альтернатив;

2) значение F зависит от числа положительных, нулевых и отрицательных значений индивидуальных функций решения, но не зависит от того, кто именно из членов группы принял то или иное индивидуальное решение;

3) если для какого-то набора индивидуальных предпочтений верно хРу, и всем участникам выбора присущи те же порядковые (ординальные) предпочтения по отношению к паре z и w, что и по отношению к паре х и у (т.е. для всякого i имеет место , когда ), то zPw;

4) если F = 0 или F = 1 и предпочтения (п – 1) участников голосования остаются неизменными, а значение индивидуальной функции решения одного участника меняется с -1 на 0 либо на 1 или же меняется с 0 на 1, то F = 1.

Условия выглядят естественными, однако в совокупности они определяют единственную из всех возможных процедур голосования.

То, что правило простого большинства отвечает перечисленным требованиям, очевидно. Теперь покажем, что если указанные требования выполняются, то коллективный выбор совершается в соответствии именно с этим правилом.

Сначала докажем от противного, что из первых трех требований следует, что если N(-1) – число голосов в пользу/, а N(1) – число голосов в пользу л*, то при N(-1) =N(1) всегда имеет место равенство:

Предположим, что при равенстве N(-1) и N(1) групповая функция решения приобретает положительное значение: F= 1. Иными словами, при одинаковом числе голосов, поданных зах и у, побеждает x.

Переименуем / в z, а x в w. Теперь голосам в пользу 2 соответствуют , а голосам в пользу w соответствует. Очевидно, что переименование альтернатив, как таковое, не меняет ни предмет, ни процедуру выбора: если до переименования побеждала альтернатива x, то теперь побеждает w.

Заменим все значения индивидуальных функций выбора, равные -1, на 1, а все значения, равные 1, на . Иными словами, представим себе, что каждый из членов группы поменял свой индивидуальный выбор на противоположный. Поскольку ранее за каждую из альтернатив высказывалось равное число участников голосования, значения N(-1) и N(1) остаются прежними. Новая ситуация отличается лишь тем, кто именно из участников высказывается за ту или иную альтернативу. В силу анонимности это не влияет на результат голосования.

Между тем в новой ситуации для всех индивидов, для которых однажды было характерно предпочтение , теперь, после взаимной замены значений 1 и -1, выполняется zRiw. В силу нейтральности, коль скоро первоначально побеждала альтернатива х, теперь побеждает z.

Итак, побеждать должна как альтернатива w, так и альтернатива z. Однако это не соответствует условию достижимости результата. Мы пришли к противоречию, опровергнув тем самым предположение, согласно которому при равном числе голосов в пользу х и у первая альтернатива способна победить.

Аналогично опровергается возможность победы второй альтернативы при N(-1) = N(1). Итак, при равном числе голосов в пользу двух альтернатив F = 0, что и характерно для правила простого большинства.

Пусть теперь N(1) = N(-1) + 1. В силу позитивного отклика и с учетом уже доказанного F = 1. По индукции без труда выводится, что исход выбора отвечает правилу простого большинства и при любом другом соотношении N(1) и N(-1). Итак, четыре названных требования (аксиомы) однозначно определяют правило простого большинства.

Прокомментируем доказанную таким образом теорему Мэя. Требование анонимности исключает влияние на выбор индивидуальных признаков голосующего, а требование нейтральности – уникальных признаков конкретной альтернативы (в ходе доказательства единственными признаками альтернатив выступают их имена, которые, однако, можно изменять, не вступая в противоречие с условиями). Тем самым формально закрепляется значимость одного только числа голосов, поданных за ту или иную альтернативу. В то же время требование достижимости результата исключает различные варианты правила квалифицированного большинства^[2].

Обратим внимание, что фактически мы пришли не только к выводу об уникальном сочетании свойств, присущем правилу простого большинства. Очевидно, что если четыре перечисленных требования дополнить хотя бы еще одним, к ним не сводящимся, то никакая процедура коллективного выбора не будет соответствовать новому набору аксиом. Нам еще предстоит обратиться к возникающей в этой связи проблеме. Пока же поставим вопрос: бесспорен ли тезис об обязательном выполнении рассмотренных требований?

Две аксиомы: анонимность и нейтральность, предполагают, что интенсивность предпочтений не учитывается. В самом деле, анонимность, по сути, означает, что, даже если предпочтения двух индивидов существенно различаются по интенсивности (скажем, один готов заплатить за победу наиболее желательной для него альтернативы намного больше, чем другой), они в одинаковой мере влияют на коллективное решение. Фактически в этом заключается принцип "один человек – один голос". Нейтральность предполагает, что две пары альтернатив трактуются единообразно, если касающиеся их предпочтения всего лишь однонаправленны, тогда как степень этих предпочтений не принимается во внимание.

Что представляет собой интенсивность предпочтений, в чем она выражается, правомерно ли сопоставление интенсивности предпочтений разных индивидов, целесообразно ли учитывать интенсивность при формировании коллективного решения – эти вопросы будут рассмотрены далее. Вместе с тем существуют процедуры коллективного выбора, отражающие определенным образом понимаемую интенсивность индивидуальных предпочтений и, следовательно, не полностью согласующиеся с аксиомами, представленными в этом параграфе. Такова, например, система Борда, с которой предстоит познакомиться несколько позже.

Теорема Мэя говорит о преимуществах правила простого большинства. Однако более 200 лет назад французский философ и математик Мари Жан Антуан Кондорсе показал, что при использовании правила простого большинства может возникать циклическое голосование.

Представим себе, что в принятии коллективного решения участвуют три индивида либо три однородные группы голосующих, каждая из которых располагает одним и тем же числом голосов. Предметом обсуждения является расходование средств, поступивших в государственный бюджет сверх первоначально планировавшейся суммы. Предполагается, что эти средства можно затратить на дополнительное финансирование только одной из трех отраслей: науки (Н), образования (О) или культуры (К). Предпочтения голосующих индивидов или групп представлены в табл. 4.1. Набор предпочтений всех участников голосования по отношению ко всем допустимым альтернативам называется профилем предпочтений.

Пусть на основе правила простого большинства происходит попарное сравнение альтернативных вариантов решения. Если начать со сравнения вариантов Н и О, то голосами первого и третьего субъектов выбора побеждает вариант Н. Далее при сравнении Н и К побеждает К благодаря голосам второго и третьего субъектов. Получается, что исход коллективного выбора – прирост ассигнований на культуру.

Однако сравним победивший вариант К с отсеянной уже на первом шаге альтернативой О. При таком сравнении преимущество получает О за счет голосов первых двух субъектов, участвующих в голосовании.

Если после этого сравнить О с Н, победу вновь одержит Н и т.д. Процесс попарного сравнения альтернатив можно продолжать до бесконечности, получая на каждом шаге новый результат и циклически повторяя чередование исходов. Оборвав же этот процесс, мы можем получить любой из исходов в зависимости от того, с какой пары альтернатив начали и на каком шаге остановились. Результат коллективного выбора оказывается, таким образом, произвольным.

Таблица 4.1. Профиль предпочтений, приводящий к цикличному голосованию

Индивиды (группы)	Наиболее предпочитаемая альтернатива	Среднеоцениваемая альтернатива	Наименее предпочитаемая альтернатива
I	Н	О	К
II	О	К	Н
III	К	Н	О

Не исключено, впрочем, что некто, заинтересованный в победе одной из альтернатив, контролирует повестку дня, т.е. располагает полномочиями определять последовательность сравнения вариантов или останавливать голосование на том или ином шаге. Если распределение предпочтений ему заранее известно либо выявилось в ходе нескольких циклов голосования, такое лицо способно целенаправленно обеспечить наиболее устраивающий его результат голосования. Последний оказывается в тоге манипулируемым.

Мы описали парадокс голосования (парадокс Кондорсе), который побуждает сделать вывод об уязвимости правила простого большинства. Выяснилось, что это правило не гарантирует транзитивности коллективного выбора. Транзитивность предполагает, что из xRy и yRz однозначно следует xRz. В нашем случае из предпочтения Н по отношению к О и предпочтения К по отношению к Н не вытекает предпочтение К по отношению к О.

Требование транзитивности представляется не менее естественным, чем четыре условия, фигурировавшие в теореме Мэя. Однако оно не обеспечивается единственным правилом, удовлетворяющим этим четырем требованиям. Следовательно, не существует процедуры коллективного выбора, удовлетворяющей всем пяти требованиям сразу.

Конечно, нетранзитивность (а значит, неустойчивость) выбора обнаруживается далеко не при всяком профиле предпочтений. Например, поменяем местами в первой строке табл. 4.1 варианты Н и О. Легко убедиться, что в этом случае при любой последовательности сравнений устойчивую поддержку получает прирост ассигнований на образование.

Имеет смысл задуматься о том, какие особенности профилей предпочтений способны гарантировать транзитивный выбор.