Построение интервальных прогнозов на основе неравенства Чебышева

Еще в начале 1970-х гг. прогнозисты начали замечать, что фактические значения, получаемые на прогнозируемом периоде, попадают в прогнозные интервалы с меньшей частотой, чем это заявлено по нормальному закону распределения случайных величин[1]. Так, в 95%-ный интервал в лучшем случае попадало 85,7% всех наблюдений, а в 90%-ный – только 80%. В 1987 г. С. Макридакис показал, что с ростом горизонта прогнозирования процент попадающих значений в доверительный интервал уменьшается[2]. Так, например, если в 95%-ный прогнозный интервал на 1 шаг вперед попадало около 82,7% всех наблюдений, то уже на 6 шагов вперед в том же интервале оказывалось лишь 73,7% наблюдений.

На основе этих эмпирических наблюдений был разработан простой метод построения прогнозных интервалов, состоящий их следующих шагов[3]:

1. На основе построенной модели на каждом наблюдении дается прогноз на один шаг вперед. На основе этого прогноза рассчитываются соответствующие "одношаговые" ошибки:

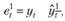
где верхний индекс определяет горизонт прогнозирования h, а нижний – номер наблюдения.

Если в ряде данных было Т наблюдений, то на основе них будут получены Т – 1 одношаговых прогноза и Т – 1 одношаговая ошибка.

2. На основе той же модели на каждом наблюдении дается прогноз на два шага вперед (например, на основе первого наблюдения дается прогноз на третье и т.д.). По полученным расчетным значениям так же рассчитываются ошибки, которые можно назвать "двухшаговыми": 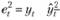, причем

число этих ошибок уже будет равно Т – 2.

3. Продолжая давать точечные прогнозы на 3, 4, ... h шагов

по аналогии с тем, как это делалось в шаге два, получаются соответствующие ряды ошибок 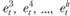. Число ошибок в каждой из этих частей будет соответственно равно Т – 3, Т-4, ..., T-h.

Получив h рядов ошибок, по каждому из них рассчитывается h CKO по стандартной формуле для каждого шага τ = 1,..., h:

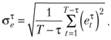(9.45)

4. Далее строится доверительный интервал. Однако в связи с тем, что интервал, построенный на основе нормального закона распределения вероятностей, на практике оказывается слишком узким, Э. Гарднер предложил вместо 2-статистики использовать неравенство Чебышева, которое записывается следующим образом[4]:

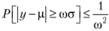(9.46)

что может быть интерпретировано следующим образом: вероятность того, что случайная величина отклонится от своего математического ожидания на величину, бо́льшую ωσ, меньше ΐ/ω2. На основе неравенства (9.46) можно сформировать прогнозные интервалы. Для начата выразим остаточную вероятность через а:

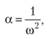(9.47)

откуда следует, что

(9.48)

Подставляя (9.47) и (9.48) в (9.49), получим

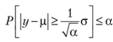(9.49)

Раскрывая модуль в (9.49), приходим к неравенству:

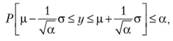(9.50)

на основе которого теперь можно построить прогнозный интервал шириной (1 – а). Применительно к нашему случаю он будет рассчитываться для каждого шага τ па основе СКО ошибок для этого шага:

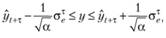
где τ = 1, 2, ..., h.

Полученные таким методом интервалы будут неровными и достаточно широкими.

Рассмотрим, каким получится интервал для метода Брауна для ряда № 41. На рис. 9.15 показаны интервалы, построенные на основе неравенства Чебышева (прерывистая линия) и (для сравнения) интервалы, построенные стандартным методом для ЕТS(A,N,N) (мелкая пунктирная линия).

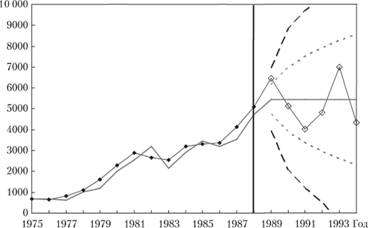
Рис. 9.15. Ряд данных № 41 (сплошная линия с точками), точечный (сплошная линия) прогноз, полученный по модели Брауна, и интервальные прогнозы, рассчитанные на основе параметрического (мелкая пунктирная линия) и непараметрического (прерывистая линия) методов

Как видим, интервалы, рассчитанные таким методом, оказались бессмысленно широкими. Вызвано это двумя причинами.

Первая заключается в том, что само неравенство Чебышева универсально и подразумевает широкие интервалы. Тут можно отметить, что в случае, если t-статистика для 5% и числа степеней свободы больше пяти уже становится меньше 2,5, то статистика, рассчитанная на основе неравенства Чебышева для той же остаточной вероятности, составит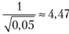

Очевидно, что именно из-за этого наблюдается такое существенное различие между этими двумя методами. Это же отмечалось в различных работах, посвященных построению эмпирических прогнозных интервалов[5].

Однако это не единственная причина получения таких неадекватно широких интервалов для нашего случая. Из-за того, что мы применили метод Брауна к нестационарному процессу, точечные прогнозы на 2, 3, ... 6 шагов вперед оказались с серьезными систематическими занижениями. В итоге и СКО в каждом из этих случаев оказалось слишком большим. Можно заключить, что в тех случаях, когда на периоде аппроксимации модель демонстрирует систематические завышения либо занижения, предложенным методом пользоваться не стоит.

Рассмотрим этот же метод построения интервалов применительно к другой модели, построенной по тому же ряду данных. Для примера мы взяли модель Хольта, которая теоретически должна давать более точные прогнозы в таких случаях, как в ряде № 41 (с возрастающей тенденцией). Далее, используя описанный в данном параграфе метод на основе неравенства Чебышева, мы оценили ошибки и их СКО. В результате всех расчетов был получен прогнозный интервал, показанный на рис. 9.16.

Как видим, из-за того, что тенденция на периоде прогнозирования сменилась, только 50% всех фактических значений попало в интервал, построенный на основе параметрического метода и предположения о нормальности распределения остатков модели. Напротив, в интервал, построенный на основе неравенства Чебышева, попали все значения.

Конечно, он все так же остается шире стандартного интервала, однако за счет более точного выбора аппроксимирующей модели интервалы оказались у́же, чем в случае с моделью Брауна.

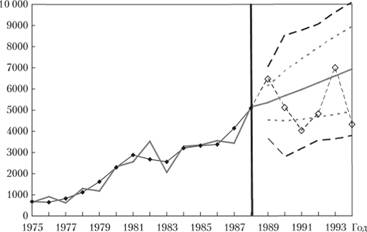
Рис. 9.16. Ряд данных № 41 (сплошная линия с точками), точечный (сплошная линия) прогноз, полученный по модели Хольта, и интервальные прогнозы, рассчитанные на основе параметрического (прерывистая линия) и непараметрического (мелкая пунктирная линия) методов

Из всего этого следует важный вывод: для того, чтобы получить адекватные прогнозные интервалы, используя описанный выше подход, нужно предварительно выбрать наиболее подходящую для ряда данных аппроксимирующую модель. Тогда мы получим, с одной стороны, широкие интервалы за счет высокого значения статистики 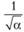, а с другой – узкие интервалы за счет небольших значений СКО для соответствующих шагов.

Для уменьшения ширины интервалов с сохранением самого принципа можно на каждом шаге τ рассчитывать свои оптимальные коэффициенты, которые гарантировали бы более точную аппроксимацию моделью ряда данных с учетом прогноза не на один шаг вперед на периоде аппроксимации, а на τ шагов вперед. Главная проблема, однако, тут заключается в том, что такой подход требует значительно больше вычислений, чем в случае с простым расчетом τ-шаговых СКО. Кроме того, такой подход требует обоснования, потому что в соответствии с общепринятым стандартом при построении модели по ряду данных предполагается, что выбранная модель оптимальна и позволяет описать исследуемый процесс наилучшим образом. Пересчет же модели с учетом прогноза на τ шагов вперед противоречит этому стандарту.