Получение стартовых значений с помощью процедуры "обратного прогноза"

Один из вариантов получения стартовых расчетных значений можно вывести с помощью процедуры, использующейся в моделях авторегрессии. Процедура эта на английском языке называется "backcasting", что дословно можно перевести как "приведение назад". Более корректным было бы назвать эту процедуру "обратным прогнозированием". Суть ее заключается в том, чтобы дать оценку значений в прошлом, используя саму модель, на основе которой мы собираемся дать прогноз. Применительно к модели Брауна формула для обратного прогноза будет иметь вид

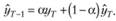(7.36)

Использование формулы (7.36) возможно благодаря тому, что модель Брауна имеет эквивалентную форму модели авторегрессии со скользящей средней, которую мы обсудим в следующей главе.

Стоит обратить внимание на то, что в формуле (7.36) для расчетов используются будущие расчетные значения, которые, в свою очередь, вообще-το должны быть получены по формуле (7.18). Получается своеобразный замкнутый круг, из которого выходят следующим образом. Вначале исследователь каким-нибудь образом задает значение (например, как равное первому фактическому значению) и на основе него строит модель до последнего наблюдения. После этого применяется формула (7.36), начиная с последнего наблюдения до самого первого. Получив таким образом первое расчетное значение, процедура построения модели по формуле (7.18) повторяется. Описанную процедуру можно провести несколько раз для того, чтобы получить значения первой точки, более адекватные для исследуемого ряда данных.

Полученная с помощью такого механизма стартовая точка оказывается фактически "выведенной" из самой модели, что по идее должно гарантировать более точное описание исходного ряда данных, а значит, и получение более точного прогноза.

Плюсом данного метода является то, что в таком случае из рассмотрения не выпадает первое значение, а ряд весов все так же сходится к единице. Минусом, однако, является сложность процедуры, в результате чего реализовать ее, например, в MS Excel, не прибегая к программированию в Visual Basic, оказывается затруднительно. Еще один минус метода заключается в том, что итоговые значения стартовой точки и оптимальной постоянной сглаживания могут зависеть от числа проведенных итераций: слишком мало итераций может означать получение неточных значений, слишком много – увеличение времени вычислений.

Подбор первого значения во время поиска оптимальной а

Последний используемый метод заключается в том, чтобы во время подбора оптимального значения постоянной сглаживания подобрать и начальную точку. Очевидно, что таким образом выбирается число, никак не привязанное к исходному ряду данных. Однако в этом случае выбирается такое число, которое обеспечивает наилучшую аппроксимацию исходного ряда данных.

Осуществить поиск стартовых значений таким методом может быть затруднительно, поэтому в качестве значений, от которых можно начать поиск оптимальных, могут выступать значения, найденные одним из описанных выше методов задания стартового значения.

Для сравнения разных методов задания стартового значения мы выбрали ряд № 41 из базы рядов М3 (вместо него можно было бы взять любой другой ряд с небольшим числом наблюдений). Из рассмотрения методов задания стартового значения мы исключили экспертный метод, так как его сложно сравнивать с другими методами – вряд ли оценка одного эксперта совпадет с оценкой другого. Для получения стартового значения, используя среднюю арифметическую по части ряда, мы выбрали первые три фактических значения.

По выбранному ряду данных мы построили шесть моделей Брауна, каждая из которых соответствовала своему методу задания стартового значения. Краткие данные по методам приведены в табл. 7.2.

Таблица 7.2

Разные методы задания стартовых значений и соответствующие им постоянные сглаживания и ошибки прогноза но ряду № 41

Метод (№)	Расшифровка метода	Значения оптимальной a	Модуль эквивалентной постоянной сглаживания |l-α|	Абсолютная ошибка прогноза на одно наблюдение	sMАРЕ но прогнозу на шесть наблюдений, %
1		1,968	0,968	1027,74	18,82
2		1,999	0,999	1018,35	18,87
3		1,968	0,968	955,26	18,82
4		1,812	0,812	997,65	18,82
5	Обратный прогноз	1.909	0,909	955,52	19,25
6	Подбор при оптимизации	1.999	0,999	1025,74	19,25

Как видим, в данном случае для всех методов задания оптимальная постоянная сглаживания оказалась лежащей в запредельном множестве. Модуль эквивалентной постоянной сглаживания практически во всех случаях близок к единице, что говорит о высокой инерционности в ряде данных. Заметно, что прогнозы на среднесрочную перспективу (шесть наблюдений вперед) получились практически одинаковыми но методам 1, 3 и 4. Методы 3 и 5 дали наиболее точные прогнозы на одно наблюдение вперед.

Графическое представление аппроксимации ряда данных и точечного прогноза на шесть наблюдений вперед приведено на рис. 7.8.

Рис. 7.8. Аппроксимация ряда данных № 41 из базы М3 и его прогноза на шесть наблюдений вперед моделью Брауна:

сплошная линия – фактические значения; прерывистая – расчетные значения

Как видим, ряд, по которому делался прогноз, носит нестационарный характер: в ряде данных имеется явная тенденция к росту. Именно поэтому оптимальная постоянная сглаживания оказалась в запредельном множестве. В целом модель при разных стартовых значениях ведет себя очень похоже, расчетные значения различаются незначительно. Оценивая только степень аппроксимации исходного ряда, сделать однозначный вывод о том, какому из методов отдать предпочтение, невозможно.

Стоит отметить, что ряд данных на периоде построения модели имел явные тенденции к росту, а вот на периоде прогнозирования стал вести себя хаотично, колеблясь относительно одного уровня ряда. Получается, что предположение о том, что в будущем сложившиеся тенденции сохранятся, в данном случае не выполняется. В такой ситуации прогноз, полученный по простой модели Брауна, скорее всего, будет более точным, нежели по каким-либо другим математическим моделям.

Оценив модель Брауна с разными методами задания по всем годовым данным М3 (ряды № 0001 – № 0645), мы получили результаты, представленные в табл. 7.3.

Таблица 7.3

Усредненные ошибки прогнозов по методу простого экспоненциального сглаживания для разных методов задания стартовых значений

Метод (№)	а>1	Горизонт прогнозирования, %
		1	2	3	4	5	6	1-6
1	500	9,23	13,72	17,90	20,24	22,94	24,81	18,14
2	492	9,21	13,66	17,91	20,16	22,76	24,52	18,04
3	500	9,23	13,72	17,90	20,24	22,94	24,81	18,14
4	498	8,55	13,01	17,25	19,65	22,31	24,15	17,49
5	483	8,76	13,06	17,22	19,61	22,30	24,22	17,53
6	498	8,80	13,15	17,38	19,72	22,42	24,26	17,62

В колонке "α >1" представлено число случаев, когда оптимальная постоянная сглаживания оказывалась лежащей в запредельном множестве. Как видим, это число велико для всех методов задания стартового значения. Учитывая, что в базе М3 представлено 645 годовых рядов данных, получить случайно такое количество постоянных сглаживания, лежащих в запредельном множестве, невозможно. Полученный результат говорит о том, что ряды в этой базе являются в своем большинстве нестационарными, а значит, для получения более точных прогнозов стоит обратиться к модификациям метода Брауна.

В той же табл. 7.3 приведены значения симметричных средних ошибок прогноза. По ним можно сделать вывод, что для большей части данных в среднем более точный прогноз дала модель Брауна с методом 4, хотя и метод обратного прогноза оказался достаточно точным (разность в sMAPE для двух методов меньше 0,04%).

Эти результаты могут служить некоторым ориентиром при принятии решения о том, какой же метод задания стартовых значений выбрать при прогнозировании. Но в каждом конкретном случае нужно принимать самостоятельное решение о том, к какому методу прибегнуть. В принятии правильного решения исследователю может помочь процедура ретропрогноза.