Показатели оценки риска корпорации
Риск характеризуют два важных аспекта[1]:
1) чувствительность (exposure) критериев деятельности к их последствиям;
2) волатильность (volatility – изменчивость) финансовых индикаторов, вероятность или частота событий.
Соответственно этому можно предложить две основные категории измерителей риска: показатели чувствительности и статистические (вероятностные) величины. Такое деление в некоторой степени является условным.
Показатели чувствительности (эластичности). Понятие эластичности широко используется при исследовании экономических процессов. Коэффициент эластичности показывает относительное изменение исследуемого экономического показателя иод действием единичного относительного изменения экономического фактора, от которого он зависит при неизменных остальных влияющих на него факторах, т.е. он является показателем силы связи, выраженным в процентах. Любые коэффициенты эластичности являются характеристиками риска.
Чем выше чувствительность результативного показателя к изменению факторного показателя, тем выше риски. При высокой чувствительности незначительное изменения влияющего фактора приведет к значительным отклонениям результативного показателя.
Операциям с финансовыми активами, вероятно, в наибольшей степени свойственна рискованность. Это связано с тем, что на финансовых рынках большую роль играют факторы субъективности, ожидания, умения добывать информацию и др. Измерители линейной чувствительности к движению финансовых переменных используются под различными обозначениями.
На рынке акций чувствительность к фактору рынка в целом (например, фондовому индексу) называется систематическим риском (systematic risk), или бетой {beta). Модель, описывающая зависимость между показателями доходности и риска индивидуального финансового актива и рынка в целом, называется моделью оценки финансовых активов САРМ (capital asset pricing model).
Теория САРМ подтверждает истину о том, что высокая доходность всегда связана с высоким риском, однако уточняет, что существенным является не собственный индивидуальный риск актива, а риск, порождаемый откликом на движения рынка.
В модели САРМ вводятся два понятия[2].
Первое – это уровень доходности рынка в целом (Rm)• Для этого можно использовать изменение какого-либо фондового индекса. Фондовый индекс дает представление о деятельности фондового рынка в целом. Как правило, абсолютные значения индексов не важны. Большее значение имеют изменения индекса с течением времени, поскольку они позволяют судить об общем направлении движения рынка, даже в тех случаях, когда цены акций в выделенной группе изменяются разнонаправленно.
Второе – это безрисковый (risk-free) уровень доходности (Rf). Безрисковый актив (risk-free asset) – актив, доходность которого определена и известна с начала периода владения этим активом. В качестве безрисковой ставки в мировой практике обычно используется ставка дохода по долгосрочным государственным долговым обязательствам (облигациям или векселям).
САРМ рассматривает доходность акции в зависимости от поведения рынка в целом. Уровень доходности рынка в целом определяется по формуле
где Ι1, Ι0 – значения фондовых индексов соответственно на конец и начало периода.
Риск в модели САРМ определяется на основании статистической информации. Проводится анализ информации о динамике фактической доходности индекса и динамике доходности одной отдельно взятой акции, обращающейся на этом же рынке. Степень зависимости доходности одной акции от уровня прибыльности всего рынка определяется путем построения регрессионных уравнений (линейная регрессия). Методика проведения корреляционно-регрессионного анализа изучается в курсе "Теория статистики". Уравнение парной линейной регрессии имеет вид
(7.1)
где у – результативный показатель; х – влияющий фактор; а, b – коэффициенты регрессии; ε – случайная погрешность.
При выявлении зависимости доходности одной акции от среднерыночной доходности в уравнении 7.1 в качестве результативного показателя выступает доходность ценной бумаги за данный период, в качестве влияющего фактора – доходность на рыночный индекс I за этот же период. Коэффициенты регрессии а, b – это и есть соответственно альфа (α) и бета (β) коэффициенты.
Доходность на индекс рынка не отражает доходности ценной бумаги полностью. Необъясненные элементы включаются в случайную погрешность рыночной модели ε.
Графическая аппроксимация фактических данных линейной функцией показана на рис. 7.3. Коэффициент регрессии β представлен на нем углом наклона линии регрессии к оси абсцисс.
Как было сказано выше, риск, связанный с инвестициями в любой рисковый финансовый инструмент, может быть разделен на два вида: систематический и несистематический. Степень несистематического риска измеряется коэффициентом альфа (α), который связан с конкретной компанией-эмитентом.
Рис. 7.3. Графическое представление взаимосвязи между доходностью отдельной акции и средней рыночной доходностью
Систематический риск обусловлен общими рыночными и экономическими изменениями, воздействующими на все инвестиционные инструменты и не являющимися уникальными для конкретного актива. Его уменьшить нельзя, но воздействие рынка на доходность финансовых активов можно измерить. В качестве меры систематического риска в САРМ используется β-коэффициент (бета), характеризующий чувствительность финансового актива к изменениям рыночной доходности. Коэффициент регрессии β служит количественным измерителем систематического риска, не поддающегося диверсификации.
Считается, что инвесторы питают неприязнь к излишнему, на их взгляд, риску, поэтому любая ценная бумага, отличная от безрисковых, может рассчитывать на признание инвесторов только в том случае, если уровень ее ожидаемой доходности компенсирует присущий ей дополнительный риск. Данная надбавка называется премией за риск.
Ценная бумага, имеющая β-коэффициент, равный 1, копирует поведение рынка в целом. Следовательно, риски, связанный с вложениями в данный финансовый актив, должны быть равны среднерыночным. Очевидно, что и премия за риск по такому активу должна быть равна среднерыночной. Доходность по государственным облигациям равна Rf. Среднерыночная доходность равна Rm. Премия за риск по среднерыночному портфелю равна (Rm – Rf).
Такую же доходность должен обеспечивать актив, имеющий β-коэффициент, равный 1.
Если β-коэффициент отрицателен, это означает, что при движении рынка в целом в одну сторону цена этой бумаги пойдет в обратную, а размер коэффициента но модулю означает кратность, т.е. если рынок изменится на 10%, а β-коэффициент равен по модулю 2, цена бумаги изменится на 30%. Если при этих же условиях β-коэффициент составляет 0,5, то цена бумаги изменится на 7,5%.
Если значение коэффициента выше 1, систематический риск такого финансового актива выше среднего. Следовательно, и премия за риск по такому финансовому активу должна быть выше среднерыночной. Акции с β-коэффициснтом больше единицы носят название агрессивные акции. Менее рисковыми являются активы, β-коэффициенты которых ниже 1 (но выше 0). Акции с β-коэффициентом меньше единицы называются "оборонительными" акциями. Риск, связанный с вложениями в акции с β-коэффициентом меньше единицы, ниже среднерыночного, следовательно, и премия за риск должна быть ниже среднерыночной.
Концепция β-коэффициентов составляют основу модели оценки финансовых активов (САРМ). Премия за риск напрямую зависит от величины β-коэффициента данного актива, так как предназначена для компенсации только систематического риска. Итак, премия за систематический риск данной ценной бумаги пропорциональна премии за риск по рыночному портфелю (индексу) с коэффициентом пропорциональности β.
где (R-Rf) – премия за систематический риск данной ценной бумаги; (Rm-Rf) – премии за риск по рыночному портфелю.
Формула определения требуемой инвесторами доходности финансового инструмента имеет вид
где R – требуемая норма доходности (ставка дисконтирования, альтернативные издержки); Rf – доходность безрисковых активов; Rm – среднерыночная доходность; β – коэффициент "бета" (измеритель риска вложений).
Отметим, что модель предлагает компенсацию только за систематический риск актива. Несистематический риск может быть устранен самим инвестором путем диверсификации своего портфеля, поэтому рынок не считает нужным устанавливать вознаграждение за этот вид риска. Взаимосвязь уровня β-коэффициента и требуемой доходности представлена на рис. 7.4.
Рис. 7.4. Взаимосвязь уровня β-коэффициента и требуемой доходности
В реальности премии за риск конкретных активов могут отклоняться от расчетных премий за систематический риск этих активов, и величина этих отклонений может быть охарактеризована как индивидуальный (несистематический) риск активов и описана α-коэффициентом, показывающим переоценку или недооценку рынком систематического риска актива:
С учетом несистематического риска, требуемая инвесторами доходность финансового инструмента имеет вид:
При построении модели САРМ было принято допущение, что связь между доходностью финансового актива и среднерыночной доходностью линейна. На практике производят статистическое уточнение оценок β- и α-коэффициентов с учетом различных моделей регрессионной зависимости.
На рынке инструментов с фиксированным доходом измерителем линейной чувствительности к движению процентных ставок является дюрация (duration).
Дюрация Маколея представляет собой средневзвешенный срок выплат по облигации, где весами являются приведенные денежные потоки, нормированные ценой инструмента. Смысл данного показателя состоит в том, что инвестор пытается с его помощью измерить риск своих вложений в облигации. Весь поток денежных выплат, связанных с облигацией, заменяют одним агрегированным платежом, который по своей финансовой значимости эквивалентен всей совокупности выплат по облигации. Дюрация – это момент времени, когда происходит этот агрегированный платеж. Чем выше дюрация, тем выше риски. Дюрация Маколея имеет размерность времени, т.е. выражается в годах.
В случае, если купонный доход выплачивается раз в год, дюрацию (D) можно определить по формуле
(7.2)
где CF – величина платежа по купону в периоде t; М – сумма погашения (номинальная стоимость облигации); п – число базовых периодов (лет) до погашения облигации; r – процентная ставка (ставка дисконтирования), равная доходности к погашению (r = ΥΤΜ).
В случае облигации с постоянным купонным доходом формула 7.2 приобретает вид:
где С – годовой купонный доход.
Во многих странах весьма распространенными являются облигационные займы с полугодовой выплатой процентов. В этом случае формула расчета дюрации имеет вид:
Пример 7.1
Облигация с номиналом 1000 руб., купонной ставкой 8% годовых и сроком погашения 4 года продается но номиналу. Купонный доход выплачивается один раз в год.
В табл. 7.1 представлен расчет денежных потоков. Отметим, что доходность к погашению данной облигации (ΥΤΜ) совпадает с купонной ставкой, так как по условию облигация продается по номиналу. В случае, если бы цена облигации была бы ниже номинала, тогда доходность к погашению превысила бы купонную доходность.
Итак, ставка дисконтирования составляет 8%.
Построение денежных потоков
Таблица 7.1
|
Год |
1 |
2 |
3 |
4 |
|
Денежный поток |
80 |
80 |
80 |
1080 |
|
Приведенный денежный поток |
|
|
|
|
Дюрация равна: 
Таким образом, средняя продолжительность платежей по четырехлетней купонной облигации составляет 3,6 года.
Приведенные выше рассуждения свидетельствуют о том, что дюрация представляет собой срок, на который фактически инвестируются деньги. Чем меньше срок инвестирования (дюрация инструмента), тем меньше процентный риск.
Дюрация зависит от трех факторов: купонной ставки, срока погашения, доходности YTM:
1) дюрация облигации с нулевым купоном всегда равна сроку ее погашения;
2) дюрация купонной облигации всегда меньше срока ее погашения;
3) величина дюрации изменяется со временем;
4) чем выше купонная ставка, тем меньше дюрация, и следовательно, риски;
5) чем выше доходность к погашению, тем меньше дюрация, т.е. рост процентной ставки на рынке приводит к уменьшению дюрации.
Показатель дюрации более корректно учитывает особенности временной структуры потока платежей. Базовой концепцией финансового менеджмента является концепция временной стоимости денег. Отдаленные платежи имеют меньший вес, и, следовательно, оказывают меньшее влияние на результат, чем платежи, более близкие к моменту оценки.
Как говорилось выше, дюрация характеризует чувствительность цены облигации к изменению процентных ставок на рынке (доходности к погашению). В общем случае процентный риск облигации может быть измерен эластичностью ее цепы по отношению к рыночной ставке r. Коэффициент эластичности показывает, на сколько процентов изменится цена облигации при изменении рыночной процентной ставки на 1%. Пусть r= YTM, тогда эластичность можно определить по формуле
где Р – цена облигации; ΥTΜ – доходность к погашению.
Как говорилось выше, связь межу ценой облигации и доходностью к погашению обратная. Это означает, что значение коэффициента эластичности всегда отрицательное.
Математически модифицированная дюрация определяется по формуле
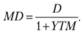
Найденное значение модифицированной дюрации может использоваться для прогнозирования изменения цены на облигацию при изменении процентных ставок:
Чем выше чувствительность цепы облигации к изменению процентных ставок, тем выше процентные риски, связанные с вложением в данный финансовый инструмент. В случае высокого значения модифицированной дюрации незначительные изменения процентных ставок приводят к значительным изменениям цены облигации.
На рис. 7.5 представлена геометрическая интерпретация модифицированной дюрации.
Пример 7.2
Рассмотрим две облигации. Кривые АС представляют собой зависимость цены облигации от изменения процентных ставок. Предположим, что в начальный момент времени при уровне процентной ставки R0 цены облигаций были одинаковы и равны Р0. Изменение процентной ставки до уровня R1 привело к снижению цен на облигации. Но так как зависимости цены облигации от уровня процентной ставки различны для этих двух бумаг, то новые цены P1 будут отличаться друг от друга. Чем больше угловой коэффициент k, тем сильнее упадет цена при росте процентной ставки, и наоборот. В нашем случае k1 > k, и следовательно, новая цена этой облигации окажется ниже, чем новая цена первой облигации. Угловой коэффициент k – это и есть модифицированная дюрация. Обратим внимание на то, что дюрация является линейной аппроксимацией и вследствие этого может быть использована при прогнозировании изменения цены при изменении процентных ставок лишь в тех случаях, когда колебания процентных ставок невелики. В противном случае величина ошибки становится значительна.
Проиллюстрируем вычисление и применение для прогнозирования изменения цен на облигацию на рассмотренном примере. Денежные потоки облигации представлены в табл. 7.1. Предположим, что инвестор, купивший данную облигацию по номиналу, ожидает роста процентных ставок на 1 процентный пункт (с 8 до 9%).
Рис. 7.5. Геометрическая интерпретация модифицированной дюрации
Таблица 7.2
Построение денежных потоков
|
Год |
1 |
2 |
3 |
4 |
|
Денежный поток |
80 |
80 |
80 |
1080 |
|
Приведенный денежный поток |
|
|
|
|
Модифицированная дюрация равна: 
Доходность к погашению изменится на 1 процентный пункт, т.е. 
Таким образом, прогнозное изменение цены облигации составит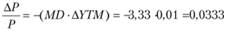 
, т.е. цена облигации снизится на 3,33% и составит 1000 • 0,9667 = 966,7 руб.
Проверим точность нашего прогноза, предположив, что ставка дисконтирования (доходность к погашению) составит не 8, а 9%.
Определим курс облигации.
Курс облигации (Р) при условии, что YTM составит 9%, равен:
Найденное значение несколько отличается от прогнозного значения. Это расхождение объясняется тем, что модифицированная дюрация является всего лишь линейной аппроксимацией чувствительности цены к изменению процентных ставок. Следовательно, она дает возможность определить приближенное изменение цены при изменении процентных ставок.
Таким образом,
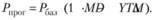
В нашем случае
Отклонение прогнозного значения цены облигации от курсовой стоимости составило: 966,7 – 967,59 = 0,89 руб.
Являясь линейной аппроксимацией, модифицированная дюрация дает хорошие результаты лишь при небольшом колебании процентных ставок на рынке. В случае значительных колебаний процентных ставок рекомендуется использовать нелинейную аппроксимацию, т.е. показатели – производные более высокого порядка.
Главная ценность дюрации состоит в том, что она приближенно характеризует чувствительность цены облигации к изменениям процентных ставок на рынке (доходности к погашению). Используя дюрацию, можно управлять риском, связанным с изменением процентных ставок.
Отметим, что мы рассмотрели использование дюрации для оценки процентных рисков облигаций, однако возможно более широкое применение дюрация для оценки процентных рисков финансовых инструментов, обладающих сходными свойствами.
На рынке производных инструментов (деривативов, derivative) чувствительность к изменению цены базового актива измеряется дельтой (delta).
Показатели – производные второго порядка – называются выпуклостью (convexity) на рынке инструментов с фиксированным доходом и гаммой на рынке деривативов. Выпуклость измеряет изменчивость дюрации по мере изменения процентной ставки. Аналогично гамма измеряет изменения дельты при изменении цены базового актива. Оба показателя измеряют чувствительность второго порядка (квадратичную чувствительность) к изменениям финансовых переменных.
Чувствительность операционной прибыли к изменению объема продаж измеряется силой действия операционного левериджа {рычага).
Операционный леверидж отображает уровень бизнес-риска, олицетворяемого с данной корпорацией. Операционный анализ деятельности корпорации был рассмотрен в гл. 5 учебника. Сила действия операционного левериджа показывает, на сколько процентов изменится операционная прибыль корпорации при изменении объема продаж на 1%. Рассчитывается сила действия операционного левериджа по формуле
Найденное значение силы действия операционного левериджа используется для прогнозирования изменения операционной прибыли при изменении объема продаж. Чем выше операционный леверидж, тем чувствительнее операционная прибыль к изменениям объема продаж. Темп прироста операционной прибыли (tοп.пр) равен произведению силы действия операционного левериджа на теми прироста объема продаж (tоб.п):
Сила действия операционного левериджа зависит от структуры операционных затрат (постоянных и переменных). Чем выше удельный вес постоянных затрат, тем выше операционный леверидж и тем выше коммерческие риски, связанные с деятельностью корпорации.
Пример 7.3
Рассмотрим расчет силы действия операционного рычага на следующем примере. Пусть известны следующие данные о деятельности корпорации (табл. 7.3):
Таблица 7.3
Исходные данные для расчета силы действия операционного левериджа, тыс. руб.
|
Показатель |
Значение |
|
Выручка |
1 759 295 |
|
Переменные затраты |
564 877 |
|
Постоянные затраты |
540 273 |
|
Операционная прибыль |
654 145 |
Маржинальный доход определяется как разница объема продаж и переменных затрат. В нашем случае маржинальный доход составляет 1 194 418 тыс. руб. Операционная прибыль меньше маржинального дохода на величину постоянных затрат. Операционная прибыль составляет 654 145 тыс. руб. Сила действия операционного левериджа составляет:
Найденное значение операционного левериджа означает, что при увеличении объема продаж на 1% операционная прибыль вырастет на 1,8259223%. В случае, если объем продаж вырастет на 10%, при данной структуре операционных затрат операционная прибыль вырастет на 18,259223% и составит 654 145 • 1,18259223 = 773 586,77 тыс. руб.
Рассчитаем операционную прибыль при росте объема продаж на 10%. Переменные затраты зависят от объема продаж, и следовательно, рост объема продаж на 10% приведет к росту переменных затрат на 10%. Маржинальный доход изменится пропорционально объему продаж (тоже на 10%). Постоянные затраты не зависят от объема продаж, и следовательно, рост объема продаж не повлияет на величину постоянных затрат. Результаты расчета представлены в табл. 7.4
Таблица 7.4
Расчет операционной прибыли при изменении объема продаж, тыс. руб.
|
Показатель |
Факт |
Прогноз |
|
Выручка |
1 759 295 |
1 935 224,5 |
|
Переменные затраты |
564 877 |
621 364,7 |
|
Маржинальный доход |
1 194 418 |
1 313 859,8 |
|
Постоянные затраты |
540 273 |
540 273 |
|
Операционная прибыль |
654 145 |
773 586,8 |
Корпорации используют операционный леверидж при управлении операционной прибылью. Изменение объема и структуры операционных затрат (постоянных и переменных) позволяет влиять на темпы изменения операционной прибыли. При положительной динамике рынка, при росте объемов продаж корпорации выгодно иметь высокий операционный рычаг, так как при этом темпы роста операционной прибыли опережают темпы роста объема продаж. Однако в случае, когда прогнозируется падение объема продаж, высокое значение операционного левериджа приведет к опережающему падению операционной прибыли. С целью снижения коммерческих рисков корпорации стремятся изменить структуру операционных затрат, уменьшая долю постоянных затрат. Снизив операционный леверидж, корпорация замедляет падение операционной прибыли при снижении объема продаж.
Чувствительность чистой прибыли к изменению операционной прибыли измеряется силой действия финансового левериджа (рычага).
Финансовый леверидж отображает уровень финансового риска, связываемого с данной корпорацией. Сила действия финансового левериджа показывает, на сколько процентов измениться чистая прибыль корпорации при изменении операционной прибыли на 1%. Сила действия финансового левериджа зависит от объема и структуры собственного и заемного капитала корпорации. Финансовый леверидж обусловлен наличием постоянных финансовых затрат. Корпорации используют денежные средства, плата за которые является постоянной (кредиты; средства, полученные путем эмиссии облигаций с постоянной ставкой купона; эмиссии привилегированных акций с постоянной ставкой дивиденда). Отметим, что в случае, когда корпорация использует денежные средства, полученные путем эмиссии привилегированных акций с постоянной ставкой дивиденда, выплачиваемый дивиденд увеличивает постоянные финансовые затраты, и в этом случае финансовый леверидж показывает чувствительность прибыли на акцию EPS к изменению операционной прибыли.
Рассчитывается сила действия финансового левериджа (DFL) по формуле
Найденное значение силы действия финансового левериджа используется для прогнозирования изменения чистой прибыли (или прибыли на акцию – при включении в состав финансовых затрат дивидендов по привилегированным акциям) при изменении операционной прибыли. Чем выше финансовый леверидж, тем чувствительнее чистая прибыль к изменениям операционной прибыли. Темп прироста чистой прибыли (tч.пр) равен произведению силы действия финансового левериджа на теми прироста операционной прибыли:
Превышение темпов прироста чистой прибыли над темпами прироста операционной прибыли обеспечивается за счет эффекта финансового рычага, рассмотренного в гл. 3 учебника.
Пример 7.4
Рассмотрим пример, представленный при расчете силы действия операционного левериджа. Рассчитаем силу действия финансового левериджа на основании следующих дополнительных данных: операционная прибыль составляет 654 145 тыс. руб.; постоянные финансовые затраты составляют 34 936 тыс. руб.; прибыль до налогообложения 619 209 тыс. руб.; чистая прибыль 49.5 367,2 тыс. руб.
Найденное значение финансового левериджа означает, что при увеличении операционной прибыли на 1% чистая прибыль вырастет на 1,0564203%. В случае, если объем продаж вырастет на 10%, при данной структуре капитала чистая прибыль вырастет на 10,564203% и составит 495 367,2 • 1,10564203 = 547 698,78 тыс. руб.
Рассчитаем чистую прибыль в случае роста операционной прибыли на 1,8259223%, что было представлено в предыдущем примере. Чистая прибыль вырастет на 1,8259223 • 1,0564203 = 1,9289413%.
Чистая прибыль составит: 495 367,2 • 1,19289413 = 590 920,6 тыс. руб. Рассчитаем чистую прибыль в случае роста операционной прибыли на 1,8259223%. Результаты расчета представлены в табл. 7.5.
Таблица 7.5
Расчет чистой прибыли при изменении операционной прибыли, тыс. руб.
|
Показатель |
Факт |
Прогноз |
|
Операционная прибыль |
654 145 |
773 586,8 |
|
Постоянные финансовые затраты |
34 936 |
34 936 |
|
Прибыль до налогообложения |
619 209 |
738 650,8 |
|
Чистая прибыль |
495 367,2 |
590 920,6 |
Финансовый леверидж является характеристикой чувствительности чистой прибыли к изменению операционной. Чем выше финансовый леверидж, тем выше финансовые риски, связанные с деятельностью данной корпорации.
Когда финансовый леверидж применяется в совокупности с операционным левериджем, полученный рычаг называется совокупным (или комбинированным). Корпорации используют для увеличения прибыли как постоянные операционные затраты, так и долговое финансирование. Чем выше доля постоянных затрат (операционных и финансовых) в структуре затрат корпорации, тем выше риски, связанные с ее деятельностью. Результатом объединения операционного и финансового левериджа является двухэтапное усиление любого изменения объемов продаж. В результате действия операционного левериджа изменение объема продаж приводит к еще большему изменению операционной прибыли (коэффициент пропорциональности – сила действия операционного рычага), в свою очередь изменение операционной прибыли приводит к еще большему изменению чистой прибыли за счет действия финансового левериджа (коэффициент пропорциональности – сила действия финансового рычага). Сила действия совокупного рычага показывает, на сколько процентов увеличится чистая прибыль при изменении объема продаж на 1%. Сила действия совокупного рычага (DTL) находиться по формуле
или 
Темп прироста чистой прибыли (tч.пр) равен произведению силы действия совокупного левериджа на темп прироста объема продаж:
При оценке рисков применяются и другие показатели, характеризующие чувствительность результативного показателя при изменении факторных показателей. В частности, одним из методов анализа рисков инвестиционных проектов является анализ чувствительности. Анализ чувствительности (sensitivity analysis) – это технология, позволяющая оценить, насколько ключевой показатель эффективности проекта (обычно это NPV или IRR) может изменяться в ответ на изменение входной переменной, если другие параметры остаются неизменными. Цель анализа чувствительности состоит в сравнительном анализе влияния различных факторов инвестиционного проекта на ключевой показатель эффективности проекта.
Статистические (вероятностные) показатели. Статистические (вероятностные) величины являются измерителями риска.
Риск – категория вероятностная, поэтому методы его количественной оценки базируются на ряде важнейших понятий теории вероятностей и математической статистики. В экономических системах в условиях риска, когда неопределенность носит вероятностный характер, а потери описываются случайной величиной, минимизация риска может состоять:
1) в минимизации математического ожидания потерь. Данный подход представляется естественным, если все возможные потери малы по сравнению с величиной собственного капитала корпорации; в противном случае данный подход неразумен;
2) минимизации квантиля распределения (например, минимизации квантиля порядка 0,95, выше которого располагаются большие потери, встречающиеся крайне редко (в нашем примере в пяти случаях из ста)). Данный подход нацелен на минимизацию больших потерь, защиту от разорения; при таком подходе средние потери могут увеличиваться, зато максимальные будут контролироваться;
3) минимизации дисперсии (или среднего квадратического отклонения), характеризующих среднее отклонение (разброс) возможных значений показателя от ожидаемого значения; данный подход нацелен на минимизацию разброса окончательных результатов, повышение определенности будущего, даже ценой повышения потерь;
4) минимизации комбинации ожидаемого значения потерь и среднего квадратического отклонения (в качестве такой комбинации может быть принята сумма математического ожидания и утроенного среднего квадратического отклонения (на основе известного правила "трех сигм"). Данный подход обусловлен тем, что управление риском – это по крайней мере двухкритериальная задача – желательно снизить ожидаемые потери (повысить математическое ожидание доходов) и одновременно уменьшить неопределенность (дисперсию);
5) максимизации математического ожидания функции полезности. Данный подход наиболее продвинутый, но и наиболее сложный; для его реализации необходимо построить функцию полезности, что является большой самостоятельной задачей.
Рассмотрим методику расчета названных показателей.
При наличии статистических данных среднее значение показателя х рассчитывается по формуле
где xi – варианты; fi – частоты (абсолютное число случаев данного варианта).
При наличии вероятностных характеристик математическое ожидание х рассчитывается по формуле
где X,- – варианты; Р, – вероятности.
Дисперсия определяется как среднее из квадратов отклонений случайной величины от ее среднего значения:
или
Расчет дисперсии можно упростить, если использовать следующую модификацию формулы дисперсии:
Дисперсия – наиболее широко применяемая оценка рассеивания случайных величин. Однако использование дисперсии не всегда удобно, так как размерность ее равна квадрату единицы измерения случайной величины. На практике результаты анализа более наглядны, если показатель разброса случайной величины выражен в тех же единицах измерения, что и сама случайная величина. Для этих целей используют стандартное (среднее квадратическое) отклонение.
Среднее квадратическое (стандартное) отклонение определяется как квадратный корень из дисперсии.
Дисперсию и среднее квадратическое отклонение используют при расчетах, связанных с организацией выборочного наблюдения, оценке полученных на основе выборки статистических показателей, построении показателей тесноты корреляционной связи, дисперсионном анализе. В том случае, когда набор данных имеет приблизительно нормальное распределение, среднее квадратическое отклонение приобретает особый смысл. Приблизительно две трети значений из такого набора данных находятся в пределах одного стандартного отклонения от среднего значения, а около 95% всех значений окажутся в пределах двух величин стандартного отклонения от среднего значения. Этот факт будет иметь большое значение при рассмотрении статистических выводов, поскольку допустимые погрешности оценок часто ограничиваются величиной 5%. И наконец, почти все данные (99,7%) будут находиться в пределах трех величин стандартного отклонения от среднего значения. При этом только 0,3% всех значений набора данных оказываются от среднего на большем, чем 3σ, удалении. Отклонение ±3σ можно считать максимально возможным. Это положение называют правилом трех сигм.
Необходимо помнить, что если набор данных не подчиняется нормальному распределению, описанные выше проценты применять нельзя. Поскольку существует множество асимметричных распределений, нельзя указать единое правило определения распределения не существует простых правил для определения части данных, попадающих в пределы одного, двух или трех стандартных отклонений от среднего значения.
Все перечисленные показатели обладают одним общим недостатком – это абсолютные показатели, значения которых предопределяют абсолютные значения исходного фактора. Это затрудняет сравнение колеблемости различных признаков. Гораздо удобней поэтому использовать относительные показатели. Именно они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей).
Коэффициент вариации дает относительную оценку вариации и получается путем сопоставления среднего квадратического отклонения со среднем уровнем явления, а результат выражается в процентах:
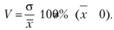
Определение коэффициента вариации особенно наглядно для случаен, когда средние величины случайного события существенно различаются.
Так как среднее квадратическое отклонения дает обобщающую характеристику колеблемости всех вариантов совокупности, то коэффициент вариации является распространенным показателем колеблемости, используемым для оценки типичности средних величин. При этом исходят из того, что если коэффициент вариации больше 33%, то это говорит о большой колеблемости признака в изучаемой совокупности. Если же коэффициент вариации не превышает 33%, то совокупность по рассматриваемому признаку можно считать однородной.
Один из способов оценки показателей распределения вероятностей основан на использовании дерева вероятностей. Построение дерева вероятностей особенно полезно в ситуациях, когда решения, принимаемые в следующие моменты времени, сильно зависят от решений, принятых ранее, и в свою очередь определяют сценарии дальнейшего развития событий. Таким образом, появляется цепочка решений, вытекающих один из другого. Дерево вероятностей представляет собой графическое или табличное изображение последовательности решений и состояний среды с указанием соответствующих вероятностей и выигрышей для всех возможных комбинаций. Дерево решений имеет вид нагруженного графа, узлы сто представляют ключевые состояния, в которых возникает необходимость выбора, а стрелки, соединяющие узлы (ветви дерева) – различные события (решения, последствия, операции), которые могут иметь место в ситуации, определяемой узлом. Каждой стрелке (ветви) дерева могут быть приписаны числовые характеристики (нагрузки), например величина платежа и вероятность его осуществления. Диаграмма в форме дерева решений используется для иллюстрации структуры риска и логики решения проекта.
Рассмотрим использование данного метода при оценке рисков инвестиционного проекта. Этот метод требует, чтобы человек, принимающий инвестиционные решения, мог предвидеть множество возможных результатов инвестиционного проекта и был в состоянии оценить вероятность наступления каждого из возможных вариантов. В этом случае указываются вероятные будущие денежные потоки рассматриваемого проекта в их связи с результатами предыдущих периодов. Таким образом в анализе можно учесть корреляцию денежных потоков, относящихся к различным периодам времени.
Если, например, оказывается, что рассматриваемый проект характеризуется высоким денежным потоком в первый период его реализации, то существуют неплохие шансы, что он будет характеризоваться хорошими денежными потоками и в последующие периоды. И наоборот, если с самого начала реализации проекта денежные потоки невысокие, то велика вероятность, что и в дальнейшем денежные потоки будут невысоки. Однако несмотря на то, что подобная связь между тем, что происходит в один период, и тем, что происходит в последующие периоды, наблюдается довольно часто, полной уверенности в этом все же нет. Если считается, что денежные потоки в разные периоды времени никак не связаны между собой, просто указывается распределение вероятностей величии денежных потоков в разные временные периоды. Если же такая взаимосвязь все же существует, ее обязательно надо учитывать.
При использовании дерева вероятностей пытаются представить ход будущих событий. Каждая полная ветвь дерева вероятностей представляет одну возможную последовательность денежных потоков. 1
Пример 7.5
Пусть первоначальные инвестиции равны 12 млн руб. Альтернативные издержки по инвестициям равны 11%. Дерево вероятностей инвестиционного проекта (денежные суммы указаны в млн руб.) представлено на рис. 7.6.
Рис. 7.6. Дерево вероятностей инвестиционного проекта
Анализ дерева вероятностей показывает, что возможны следующие сценарии:
1. 0-1-3;
2. 0-1-4;
3. 0-2-5;
4. 0-2-6.
Общее число возможных серий потоков денежных средств т = 4. Рассчитаем чистые приведенные стоимости и вероятности реализации для каждой возможной серии потоков денежных средств:
1) 
;
2) 
;
3) 
;
4) 
.
Рассчитаем ожидаемую чистую приведенную стоимость проекта.
Дисперсию:
Среднее квадратическое отклонение:
Коэффициент вариации:
Слабым местом данного метода является его субъективность. Разные оценки возможных исходов и их вероятностей могут привести к совершенно разным результатам.
Если рассматривается крупный инвестиционный проект, при оценке риска желательно не ограничиваться анализом чувствительности и сценариев. В условиях высокой неопределенности и риска предпочтительнее использовать альтернативные методы, одним из которых является метод Монте-Карло. Симуляция Монте-Карло является значительно более сложной технологией, чем анализ сценариев, однако электронные средства делают этот процесс вполне осуществимым. Метод имитационного моделирования Монте-Карло создает дополнительную возможность при оценке риска за счет того, что делает возможным создание случайных сценариев.
При использовании метода Монте-Карло строятся последовательные сценарии с использованием исходных данных, которые по смыслу проекта являются неопределенными, и потому в процессе анализа полагаются случайными величинами. Компьютер начинает работу с выбора случайного значения каждого из переменных параметров проекта – цены продукции, переменных затрат, объема продаж и т.д., причем процесс имитации осуществляется таким образом, чтобы случайный выбор значений из определенных вероятностных распределений не нарушал существования известных или предполагаемых отношений корреляции среди переменных. Затем для данного сценария находится значение результирующего показателя (например, NPV), которое записывается в память компьютера. Далее случайным образом выбирается другой набор случайных переменных и вычисляется результирующий показатель (в нашем примере – NPV) для второго сценария. Этот процесс повторяется множество, иногда несколько тысяч, раз. Результаты всех имитационных экспериментов объединяются в выборку и анализируются с помощью статистических методов с целью получения закона распределения вероятностей результирующего показателя (NPV). В отдельных случаях закон распределения не определяют, а ограничиваются моментами, характеризующими статистические параметры объекта. Среднее значение выборки используется как оценка среднего значения чистой текущей стоимости проекта, а среднее квадратическое отклонение (или коэффициент вариации выборки) используется для измерения его риска. В качестве меры риска в инвестиционном проектировании целесообразно также использовать вероятность получения отрицательного значения NPV.
Результат анализа риска выражается нс каким-либо единственным значением NPV, а в виде вероятностного распределения всех возможных значений этого показателя. Следовательно, потенциальный инвестор с помощью метода Монте-Карло будет обеспечен полным набором данных, характеризующих риск проекта. На этой основе он сможет принять взвешенное решение о предоставлении средств.
Процесс анализа риска может быть разбит на следующие стадии.
1. Строится прогнозная модель, определяющая результирующий показатель как функцию от переменных и параметров. В качестве базовой модели для анализа инвестиционного риска обычно используется модель расчета показателя NPV.
2. Проводится анализ выбранных переменных. Из их числа выбирают только те, изменение которых существенным образом влияет на результат (отбор может производиться, например, с помощью анализа чувствительности).
3. Определяется вероятностный закон распределения выбранных переменных.
4. Устанавливаются границы диапазона значений переменных.
5. Определяются корреляционные связи между выбранными переменными (фактически наличие корреляции ограничивает случайный выбор отдельных значений для коррелированных переменных; две коррелированные переменные моделируются так, что при случайном выборе одной из них другая выбирается не свободно, а в диапазоне значений, который управляется смоделированным значением первой переменной)
6. Проводятся имитационные прогоны (генерируются случайные сценарии, основанные па наборе допущений; всю работу проводит компьютер).
7. Проводится статистический анализ результатов имитации.
Вперед категория – структурные средние. Среди структурных средних наиболее распространены мода и медиана. Мода отражает наиболее часто встречающееся значение признака в вариационном ряду. Медиана – значение варьирующего признака, приходящегося на середину ранжированной совокупности. Таким образом, в ранжированном ряду распределения одна половина ряда имеет значения признака меньше медианы, а вторая – больше медианы.
Если же возникает необходимость изучить структуру ряда более подробно, вычисляют квантили, или градиенты. Квартили, квинтили, децили – частные случаи квантилей.
Квартилями называются такие значения признака, которые делят распределение на четыре равные части. Обозначим значения xi, делящие вариационный ряд на четыре равные части через Q1, Q2, Q3• Ниже первой квартили Q1 лежит 25% значений хi•. Ниже второй квартили Q2 лежит половина значений xi т.е. вторая квартиль делит распределение пополам и совпадает с медианой. Между второй Q2 и третьей Q3 квартилями лежит 25% значений х,, а оставшиеся 25% значений хi лежит выше третьей квартили Q3. Q3 называется верхней квартилью, Q1 – нижней квартилью.
Квинтили делят распределение на пять равных частей, децили – на десять.
В ряду квантильных мер риска необходимо выделить такие показатели, как value-at-risk и shottfall-at-risk.
Утверждение о том, что портфель имеет определенное значение VAR, фактически означает следующее: в течение промежутка времени Т с доверительной вероятностью Р абсолютная величина убытка по портфелю не может быть больше, чем VAR (доход по портфелю не может быть меньше, чем – VAR), при этом абсолютная величина убытка, превосходящая VAR, также не исключена, однако такой убыток может случиться лишь с малой вероятностью (1 – Р). Уровень доверия (вероятность) выбирается по-разному, в зависимости от предпочтений по риску, выраженного в регламентирующих документах надзорных органов, или в корпоративной практике, отражая оценки менеджеров.
VAR является достаточно распространенной мерой риска портфеля, которая имеет однако ряд существенных недостатков.
1. В отличие от дисперсии, VAR не обладает свойством аддитивности. Это означает, что даже если известны величины VAR составляющих портфель активов и коэффициенты корреляции между активами, то в общем случае на основании этих данных невозможно рассчитать VAR портфеля. Это связано с тем, что VAR является квантильной оценкой, поэтому ее нельзя вычислить без знания закона распределения дохода портфеля. Но при суммировании доходов активов законы их распределения могут деформироваться, поэтому распределение дохода портфеля может сильно отличаться от распределений доходов составляющих его активов.
2. VAR не учитывает возможных больших убытков, которые могут произойти с малыми вероятностями.
3. При указании в качестве меры риска только величины VAR отсутствует информация о виде распределения доходов портфеля. При этом, если распределение доходов портфеля является островершинным (эксцесс больше 3), то риск портфеля будет недооцениваться, а если распределение доходов – плосковершинное (эксцесс меньше 3), то риск будет переоцениваться.
Существуют две основных группы подходов к оценке VAR. Первая группа основана на локальном оценивании (local valuation), наиважнейшим ее примером является параметрический дельта-нормальный метод (delta-normal method)[3]. Дельта-нормальный метод предполагает, что доходности активов нормально распределены. Вторая группа использует полное оценивание (full valuation), к пей относятся метод исторических симуляций (historical simulation method), стресс-тестинг (stress-testing), метод симуляций Монте- Карло (structured Monte-Carlo).
При использовании тех или иных подходов необходимо верифицировать модель. Риск, связанный с применением неадекватной модели, называется модельным риском (model risk).
VAR используется для риск-менеджмента в качестве базы для лимитов по открытым позициям, для расчета достаточности капитала, для оценки стоимости портфеля, для оценки доходности с учетом риска и т.д.
С учетом перечисленных недостатков VAR хотелось бы иметь характеристику риска портфеля, которая описывает реализующиеся с малыми вероятностями аномально большие убытки. Такой мерой риска является Shortfall-at-risk (SAR). SAR – это ожидаемое значение убытка портфеля при условии, что абсолютная величина убытка превосходит VAR.
Совместное использование в качестве мер риска VAR и SAR позволяет иметь более полную информацию о хвостах распределения доходов портфеля. При этом представляется целесообразным рассчитывать эти величины одновременно для нескольких различных значений доведоверительной вероятности Р (например, 0,950, 0,975, 0,990, 0,999). Методика вычисления данных показателей подробно изложена, в частности, С. В. Булашевым в книге "Статистика для грейдеров"[4].
К прочим показателям, которые также фактически являются измерителями риска, относятся: запасы или разрывы (gap) или коэффициенты (ratio) ликвидности (liquidity), финансовой устойчивости, косвенные показатели: рейтинги ценных бумаг, заемщиков, рынков, государств (в том числе факторная модель кредитного риска (Z-score) Альтмана); премии за риск, содержащиеся в доходности различных активов; котировки производных финансовых инструментов (опционов, фьючерсов, свопов и т.д.); параметры дефицита (длина и продолжительность очереди, объем запасов и т.п.), и т.д. Все эти показатели статистическими, экспертными, либо рыночными оценками характеризуют риски активов. Некоторые из этих показателей будут рассмотрены в параграфе 7.3.
В ходе исследования, проведенного PwC[5], респондентам был задан вопрос о том, каким образом осуществляется оценка финансовых рисков. Согласно результатам опроса, большинство респондентов (73%) производят оценку финансовых рисков самостоятельно, без привлечения сторонних компаний; 15% компаний пользуются услугами банков и 12% – услугами консалтинговых компаний.
Что касается методов оценки финансовых рисков, то более половины опрошенных компаний (61%) отметили, что используют анализ чувствительности, 50% респондентов применяют сценарное моделирование, только 11% компаний используют d/Синдикаторы, 66% компаний при оценке финансовых рисков используют более двух различных методов (рис. 7.7).
Рис. 7.7. Методы оценки финансовых рисков, % компаний
Разнообразные формальные методы оценивания рисков и управления ими во многих случаях не могут дать однозначных рекомендаций. В конце процесса принятия решения – всегда человек, менеджер, на котором лежит ответственность за принятое решение. В условиях нестабильной среды, когда повторение экономической ситуации в одних и тех же условиях практически неосуществимо и отсутствует информация о возможности появления рисковых событий, можно и нужно использовать субъективные методы экспертных оценок, суждений и личного опыта эксперта, мнения финансового менеджера и т.д. Не исключено и привлечение эвристических правил, представляющих совокупность логических приемов отыскания истины.
Методы экспертной оценки риска представляют собой комплекс логических и математических процедур, направленных на получение от специалистов-экспертов информации, ее анализ, обобщение с целью выбора рациональных решений. Процедуры экспертного оценивания естественно применять не только на конечном, но и на всех остальных этапах анализа рассматриваемого проекта, используя при этом весь арсенал теории и практики экспертных оценок. Методы экспертных оценок можно разделить на две группы.
1. Методы коллективной работы экспертной группы, предполагающие формирование общего мнения в ходе совместного обсуждения последствий предпринимательской деятельности (методы мозговой атаки, сценариев, деловых игр, совещаний и суда).
2. Методы получения индивидуального мнения членов экспертной группы, основанные на предварительном сборе информации от экспертов, опрашиваемых независимо друг от друга, с последующей обработкой полученных данных (методы анкетного опроса, интервью, Дельфи).
Все используемые методики оценки рисков можно разбить на три категории, основные достоинства и недостатки которых представлены в табл. 7.6.