Оценка риска инвестиций

Как отмечалось, вкладывая деньги в тот или иной инвестиционный объект, инвестор может лишь с определенной долей уверенности прогнозировать будущую отдачу инвестиций. Для количественного описания степени объективной возможности наступления того или иного случайного события r вводится специальная числовая функция Р(r), называемая вероятностью события r. В применении к доходности r можно считать, что вероятность показывает относительную частоту появления того или иного значения r.

Так, предположим, что нас интересует, какую доходность обеспечит выбранный нами инвестиционный объект (положим, акция) за будущий холдинговый период (день). Чтобы сделать такую оценку, пойдем следующим путем: выберем в прошлом 100 дней и вычислим доходность акции за каждый день. Полученные результаты сведем в табл. 1.1.

Таблица 1.1

Данные для расчета вероятности

Доходность	Количество наблюдаемых результатов	Вероятность
r1= 5%	15	P1=0,15
r2=7%	20	P2= 0.20
r3= 10%	25	P3=0,25
r4=12%	30	P4= 0,30
r5 = 15%	10	P5= 0,10

Вероятность в данном случае показывает относительную частоту появления ожидаемой величины: вероятность доходности r1 находится как отношение числа наблюдаемых подобных результатов к общему числу наблюдаемых событий: Р1 = 15/100 = 0,15.

Для вероятностей используют пять основных правил:

1) вероятность никогда не бывает отрицательной величиной;

2) вероятность не может быть больше единицы (или 100%);

3) сумма вероятностей всех возможных результатов наблюдений равняется единице;

4) если результат события вполне предопределен, то вероятность этого события равна единице; никакой другой результат невозможен;

5) если событие не может произойти, то считается, что его вероятность равна нулю.

В силу неопределенности доходности акции за будущий холдинговый период (сегодня мы не в состоянии предвидеть события в будущем) ичнвестор должен оценивать среднюю, или ожидаемую, доходность. Ожидаемая доходность Е(r) – это взвешенная средняя величина всех возможных значений доходности, где вес каждой доходности определяется вероятностью ее появления. Иными словами, если было проведено п измерений величины r и вероятность доходности rt равна Рt то

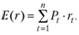(1.4)

Вычислим ожидаемое значение доходности в рассматриваемом примере:

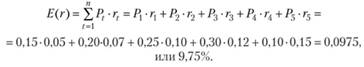
На основании этого результата можно утверждать, что по окончании будущего холдингового периода реализованная доходность оцениваемой акции с определенной вероятностью окажется равной 9,75%, т.е. имеется риск того, что реализованная доходность отклонится от данной величины.

В математической статистике количественно степень риска инвестиций оценивают с помощью специальной величины – дисперсии σ'2, которая представляет собой средневзвешенное значение квадратов отклонений наблюдаемых величин доходности rt от средней (ожидаемой) величины Е(r):

Дисперсия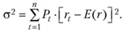 (1.5)

Для нашего примера

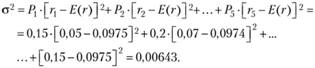
Чем выше дисперсия, тем выше разброс вероятных событий и тем выше риск инвестиций.

Чаще для количественного измерения риска используют величину стандартного (среднеквадратичного) отклонения σ. По определению σ равняется квадратному корню из величины дисперсии:

(1.6)

Стандартное отклонение σ имеет размерность доходности г (процент) и определяет некоторый стандартный среднеквадратичный интервал рассеивания случайных величин rt симметричный относительно ожидаемого (среднего) значения доходности Е(r). Для нашего примера

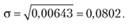
Как и в случае дисперсии, можно утверждать, что чем выше среднеквадратичное отклонение случайных величин доходности, тем более рискованными являются инвестиции.

Длительность шагов расчета, за которые проводится расчет дисперсии и стандартного отклонения, может быть различной, и эта длительность может не совпадать с тем холдинговым периодом, за который инвестору хотелось бы оценить риск инвестирования. Например, расчет дисперсии (стандартного отклонения) проведен за промежуток времени t (квартал), т.е. вычислены величины 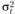и . И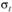нвестора же интересует уровень риска за другой промежуток времени Т (предположим, год).

Тогда для вычисления дисперсии и стандартного отклонения за промежуток времени Т используют следующие формулы:

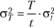
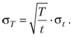
Пример 1.1. Пустьв ходе вычисления дисперсии за квартал получена величина . Каков будет уровень риска за год, если

рыночные тенденции, учитываемые за квартал, не изменятся и в течение года.

Решение

Имеем:

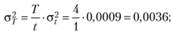
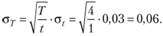
В дальнейшем будем оперировать случайными величинами доходности, полагая, что эти случайные величины распределены по нормальному (гауссовскому) закону. В случае нормального распределения доходности r вероятность попадания случайной величины r в интервал [r1; r2] можно найти по формуле

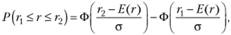(1.7)

где Ф(r) – функция распределения случайной величины. Она определяет вероятность того, что случайная величина R примет значение, которое меньше фиксированного действительного числа г, т.е. Ф(r) = P(R<r). Значения функции Ф(r) находят по табл. П1 (см. приложение). При расчетах следует учитывать, что Ф(-r) = 1-Ф(r).

Пример 1.2. Ответим на следующий вопрос: какова вероятность того, что для рассмотренной выше акции доходность r, будет отклоняться от ожидаемого (среднего) значения на 5%, т.е. какова вероятность того, что доходность акции будет лежать в пределах [4,75%; 14,75% |?

Решение

Воспользуемся формулой (1.7):

Поскольку в таблицах приводятся величины функции Ф(r) только для значений r, округленных до второго знака (Ф(0,62),

Ф(0,63) и т.д.)" то, чтобы вычислить величину Ф(0,6234), используют следующий подход:

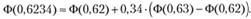
По табл. П1 находим, что Ф(0,62) = 0,7324, а Ф(0,63) = 0,7357. Тогда вероятность попадания доходности r в интервал [4,75%; 14,75%] составит

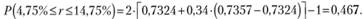
Следовательно, для рассматриваемого примера существует вероятность 46,7% (Р= 0,467) того, что случайная величина η отклонится от ожидаемого (среднего) значения Е(r) = 9,75% на 5%.

Отталкиваясь от формулы (1.7), можно показать, что с ростом величины σ вероятность попадания доходности r в заданный интервал уменьшается, т.е. увеличение среднеквадратического отклонения повышает неопределенность и степень риска инвестиций.