Оценка облигаций

Принимая решение об инвестировании средств в долговые ценные бумаги, инвестор должен сопоставлять расходы, которые он вынужден осуществлять в настоящее время, с ожидаемыми результатами, т.е. доходами.

Владельцев облигаций, главным образом, интересуют: доходность и курс облигаций.

Как и большинство ценных бумаг, облигация может приносить доход двумя способами. Во-первых, в форме процентной ставки (купона) по займу, которая в большинстве случаев представляет собой фиксированную годовую величину. Во-вторых, можно достичь прироста капитала в виде разницы между ценой, по которой инвестор продает облигацию, и ценой приобретения облигации.

Облигации с момента их эмиссии и до погашения продаются и покупаются по установившимся на рынке ценам.

Рыночная цена – цена, по которой облигации, оставаясь важнейшим объектом долгосрочных инвестиций, продаются и покупаются на денежно-кредитном рынке с момента их эмиссии до погашения.

Поскольку номиналы у разных облигаций существенно различаются между собой, то часто возникает необходимость в сопоставимом измерителе рыночных цен. Таким показателем облигации служит ее курс, т.е. цена одной облигации в расчете на 100 ден. ед. номинала:

где К – курс облигации; Р – рыночная цена; N – номинал облигаций.

Например, если облигация номиналом 1000 долл. продается за 980 долл., то ее курс составит 98^[1].

Расчет рыночной стоимости облигаций Р основан на принципе дисконтирования доходов, так как именно дисконтированная (приведенная) стоимость всех доходов, которую предполагает получить инвестор с момента покупки облигации и до ее погашения, определяет рыночную цену облигации на момент ее приобретения.

Бескупонные облигации. Допустим, что сегодня приобретается чисто дисконтная, или бескупонная, облигация, эмитент которой обещает выплатить некоторую сумму в момент ее погашения. Обещаемая будущая выплата – это номинальная стоимость, или номинал облигации, N.

Разность между номиналом и текущей ценой продажи называется облигационной скидкой (облигационным дисконтом).

Так как облигация с нулевым купоном создает только один будущий денежный поток доходов, равный ее номинальной стоимости, то цепа Р есть приведенная стоимость номинальной стоимости облигации. На рис. 3.5 показаны денежные потоки для чисто дисконтной облигации.

Если номинальная стоимость должна быть получена через п лет от настоящей даты, то при годовой процентной ставке для дисконтирования г цена чисто дисконтной облигации составит

где – дисконтированная стоимость одной будущей денежной единицы, например 1 долл. США.

Рис. 3.5. Денежные потоки для чисто дисконтной облигации

Купонные облигации

Бо́льшую часть облигаций международных компаний представляют купонные облигации, по которым, как правило, один или два раза в год производятся купонные выплаты, а в момент погашения они гасятся по номиналу. Сущность оценки стоимости облигации состоит в том, что в течение срока существования облигации ее владелец должен получить ту же сумму, которую он вложил в облигацию при покупке.

Особенность состоит в том, что совокупность платежей, которые должен получить владелец облигации, растянута во времени, и, следовательно, все будущие денежные потоки следует продисконтировать к моменту времени оценки стоимости облигации. В качестве показателя дисконта необходимо принимать доходность аналогичных финансовых инструментов со сравнимым риском, иными словами – альтернативных инвестиций.

Допустим, что сегодня приобретается облигация номинальной стоимостью N и сроком погашения через п лет. Предположим, что в конце каждого года до срока погашения по облигации выплачивается купонный доход С, рыночная ставка доходности r.

Тогда приведенная стоимость потока купонных платежей

где – дисконтированная стоимость ежегодной ренты (аннуитета) в 1 ден. ед.

Приведенная стоимость возвращаемых в момент погашения облигации платежей по номиналу составит

Принимая во внимание, что цена купонной облигации должна быть равна сумме величин приведенной стоимости выплат, которые надлежит произвести по облигации, цену купонной облигации можно рассчитать следующим образом:

Отметим при этом еще раз, что купонные выплаты но облигации представляют собой обычный аннуитет, приведенную стоимость которого можно рассчитать по формуле

В данной формуле важно также отметить, что п – количество лет, которые остаются до погашения облигации. Например, облигация выпущена на 7 лет, однако 2 года уже прошло. Определяя курсовую стоимость такой облигации, следует принять п – 5. Это вытекает из принципа дисконтирования будущих доходов: в данном случае облигация принесет доходы инвестору только за оставшиеся 5 лет. Графическая иллюстрация денежных потоков для купонных облигация дана на рис. 3.6.

Рис. 3.6. Денежные потоки для купонной облигации

Пример. Пусть номинальная стоимость облигации N = 1000 долл. США. Помимо этого в контракте указываются: количество дет до погашения п = 20 лет; купонная ставка с = 14% годовых; периодичность выплаты процентов т = 1 год.

Оцените рыночную стоимость облигации в изменяющихся условиях фондового рынка.

Решение.

1. Допустим, что в момент эмиссии облигации рыночная процентная ставка равна купонной (с = r= 14%). Тогда цена рассматриваемой облигации

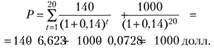
2. Предположим, прошло четыре года. Инвестор получил 4 купона, т.е. 4 раза по 140 долл. До погашения осталось 16 лет. Рыночная процентная ставка не изменилась, и она составляет 14% годовых. Снова оценим стоимость облигации но прошествии 4 лет:

Стоимость облигации закономерно осталась равной ее номиналу, так как ситуация на рынке не изменилась. Такая же ситуация сохранится на протяжении всего срока до погашения облигации, если процентная ставка на рынке не изменится.

3. Предположим теперь, что средняя рыночная процентная ставка выросла на два процентных пункта (п.п.) и составляет 16% годовых.

До погашения облигации по-прежнему остается 16 лет. В этом случае стоимость рассматриваемой облигации

Это снижение стоимости имеет свое логическое объяснение. Поскольку по аналогичным финансовым инструментам инвесторы в рассматриваемых условиях получают 160 долл. в год на каждые инвестированные 1000 долл., владельцы данной облигации будут стремиться избавиться от нее. Это создаст на фондовом рынке повышенное предложение, вследствие чего цена на рассматриваемые облигации будет снижаться пока нс достигнет равновесного состояния на уровне 886,6 долл.

Итак, мы показали, что, имея облигацию номиналом 1000 долл., владеем суммой 886,6 долл. Это приносит 140 долл. дохода в год, что соответствует уровню доходности 16% в год.

4. Если рассмотреть противоположную ситуацию, когда средняя рыночная процентная ставка уменьшилась и составляет, к примеру, 12%, то следует ожидать повышения рыночной цены этой облигации, так как она обеспечивает доходность, бо́льшую, чем средняя по рынку, (14% > 12%).

Если купон выплачивается несколько раз в год (т > 1), формула для расчета стоимости облигации будет иметь вид

5. Для условий примера, когда рыночная процентная ставка составляет 12% годовых и до погашения остается 16 лет, при полугодовой выплате процентов () получим

В этом случае стоимость облигации оказалась несколько выше, так как процентные платежи инвестор получает более часто.

Оценка бессрочной облигации

Облигации этого типа предусматривают неопределенно долгую выплату дохода в установленном размере. Облигация нс может быть погашена, т.е. доход инвестора складывается лишь из периодических поступлений в виде купонного дохода. В условиях неизменности купонного дохода денежный поток, инициируемый облигацией, имеет вид бессрочного аннуитета, а ее стоимость может быть рассчитана как Р= С/r.

Соотношение между величинами купонной ставки, требуемой доходности и ценой

Рыночным доходностям (r), как было показано на примере, свойственно постоянно изменяться. Единственная переменная, которая изменяется при этом, чтобы соответствовать новой требуемой доходности, является цена облигации. В частности, если купонная ставка равна требуемой доходности, цена облигации будет равна ее номиналу.

Как только в данный момент времени рыночная доходность поднимается выше купонной ставки, цена облигации "приспосабливается" к новым условиям таким образом, чтобы инвестор, приобретающий облигацию, мог получить от ее покупки определенную дополнительную выгоду. Если бы цена такой облигации не менялась, инвесторы бы отказывались от приобретения облигации, предлагающей доходность ниже рыночной. Таким образом, недостаток спроса приводит к падению цены и росту доходности облигации. Именно так и происходит на практике падение цены облигации ниже уровня ее номинала.

Прирост капитала инвестора, реализуемый им посредством удержания такой облигации до даты погашения, – форма компенсации, предлагаемой инвестору, владеющему облигацией с купонной ставкой ниже требуемой доходности.

Если облигация продастся но цене, более низкой, чем се номинальная стоимость, говорят, что облигация была продана с дисконтом.

Если требуемая рыночная доходность меньше купонной ставки, облигация будет продаваться по цене, более высокой, чем ее номинальная стоимость. Это происходит потому, что инвестор, приобрети он облигацию по номиналу, получил бы купонную ставку, превышающую справедливую рыночную доходность. В результате цена на облигацию со столь привлекательной доходностью пошла бы вверх. Цена при этом будет расти до тех пор, пока доходность облигации не совпадет с требуемой доходностью рынка.

Про облигацию, цена которой превышает се номинальную стоимость, говорят, что она продастся с премией.

Отношения между величинами купонной ставки, требуемой доходности и цены облигации можно конкретизировать с помощью следующих правил.

1. Если требуемая доходность равна купонной ставке по облигации, то ее цена равна номиналу.

2. Если требуемая доходность выше, чем купонная ставка по облигации, то цена облигации меньше номинала, т.е. облигация продается с дисконтом к номиналу.

3. Если требуемая доходность меньше, чем купонная ставка, то ее цена больше номинала, т.е. облигация продается с премией к номиналу.

4. Цены облигаций изменяются в направлении, противоположном направлению изменения доходностей.

Цена как функция срока до погашения

Что происходит с ценой облигации, если в течение периода между приобретением облигации и датой ее погашения требуемая доходность (процентная ставка) не меняется?

Если при этом купонная ставка равна требуемой доходности, то, как было установлено выше, облигация будет продаваться по номиналу, и ее цена не будет изменяться по мере приближения даты погашения. Однако цена облигации не будет оставаться неизменной, если облигация продается с дисконтом или с премией. Цена любого выпуска облигаций к моменту погашения их достигает номинала N (рис. 3.7).

Отметим, что цена облигации, продающейся с дисконтом, при условии неизменной требуемой доходности растет. Обратный процесс происходит с ценой облигации, продающейся с премией. Цена обеих облигаций в момент погашения равна номинальной стоимости.

Рис. 3.7. Цена как функция срока до погашения: ценные бумаги, торгуемые с премией, по номиналу и с дисконтом

Заметим также, что симметричные разности между требуемой доходностью и купонной ставкой преобразуются в асимметричные разности между ценой облигации и ее номинальной стоимостью. В частности, цена облигации при снижении доходности растет в бо́льшей степени, чем она падает при росте доходности.