Оценка качества построенных моделей

Модель считается хорошей со статистической точки зрения, если она адекватна исследуемому процессу, т.е. достаточно надежно отображает детерминированную составляющую процесса и достаточно точна. Если детерминированная составляющая процесса достоверно отображена моделью, то после ее выделения из исходного временного ряда останется временной ряд, компонентами которого являются значения, образованные вследствие воздействия на процесс случайных субъективных факторов, т.е. останется временно́й ряд, состоящий из случайных чисел.

Проверка адекватности модели реальному явлению в этом случае заключается в проверке соответствия временного ряда, состоящего из значений остаточной компоненты, ряду статистических гипотез, т.е. проверке того, насколько компоненты этого ряда являются случайными величинами. Если проверка всех нижеперечисленных гипотез будет положительна, то это означает, что члены остаточной компоненты действительно являются случайными величинами и детерминированная составляющая процесса правильно отображена моделью.

Значения остаточной компоненты получают как разность между фактическими наблюдениями временного ряда и расчетными значениями этого же ряда, вычисленными с использованием модели, т.е. , здесь значения остаточной компоненты. К наиболее важным гипотезам, которым должна отвечать совокупность из последовательных значений остаточной компоненты относятся: равенства нулю их математического ожидания, независимость последовательных значений остаточной компоненты, их случайность и подчиненность нормальному закону распределения.

Проверка равенства математического ожидания значений остаточной компоненты нулю осуществляется путем проверки соответствующей нулевой гипотезы . С этой целью строится t-статистика:

(13.13)

где – среднее арифметическое значение уровней ряда

остаточной компоненты ; – среднее квадратическое отклонение для этой последовательности, рассчитанное по формуле для малой выборки.

На уровне значимости гипотеза отклоняется, если , где – критерий распределения Стьюдента с доверительной вероятностью () и степенями свободы .

Для проверки случайности уровней ряда может быть использован критерий "пиков", или критерий поворотных точек.

• Значение случайной переменной считается поворотной точкой, если оно одновременно больше (меньше) соседних с ним элементов.

Если остатки случайны, то поворотная точка приходится примерно на каждые 1,5 наблюдения. Если же их меньше, то последовательные значения случайной компоненты коррелированны. Критерий случайности отклонений от тренда при уровне вероятности 0,95 можно представить как

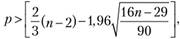(13.14)

где р – фактическое количество поворотных точек в случайном ряду; 1,96 – квантиль нормального распределения для 5%-ного уровня значимости. Квадратные скобки здесь так же означают, что от результата вычисления следует взять целую часть. Если неравенство не соблюдается, то ряд остатков нельзя считать случайным (т.е. он содержит регулярную компоненту) и, стало быть, модель не является адекватной.

Проверка условия независимости последовательных значений остаточной компоненты, т.е. наличие (отсутствие) автокорреляции между ними проверяют с помощью критерия Дарбина – Уотсона.

Численное значение коэффициента

(13.15)

где .

Значение dw статистики близко к величине 2(1 – r(1)), где r(1) – выборочная автокорреляционная функция остатков первого порядка. Таким образом, значение статистики Дарбина – Уотсона распределено в интервале 0÷4. Соответственно, идеальное значение статистики – 2 (автокорреляция отсутствует). Меньшие значения критерия соответствуют положительной автокорреляции остатков, большие значения отрицательной. Статистика учитывает только автокорреляцию первого порядка. Оценки, получаемые по критерию, являются не точечными, а интервальными. Верхние () и нижние () критические значения, позволяющие принять или отвергнуть гипотезу об отсутствии автокорреляции, зависят от количества уровней динамического ряда. Значения этих границ для уровня значимости α = 0,05 даны в специальных таблицах.

При сравнении расчетного значения dw статистики с табличным могут возникнуть такие ситуации: ряд остатков не коррелирован; – остатки содержат автокорреляцию; – область неопределенности, когда нет оснований ни принять, ни отвергнуть гипотезу о существовании автокорреляции. Если d > 2, то это свидетельствует о наличии отрицательной автокорреляции. В этом случае перед сравнением с табличными значениями dw (табл. 13.3) критерий следует преобразовать по формуле .

Таблица 13.3

Проверка статистической значимости dw статистики

№ п/п	Величина dw	Результат
1		Нулевая гипотеза отвергается, фиксируется наличие положительной автокорреляции остатков. Нулевая гипотеза отвергается, фиксируется наличие отрицательной автокорреляции остатков
2		Неопределенность
3		Принимается нулевая гипотеза
4		Преобразование критерия dw' = 4 – dw

Если ситуация оказалась неопределенной (),

то применяют другие критерии. В частности, можно воспользоваться первым коэффициентом автокорреляции

(13.16)

Для принятия решения о наличии или отсутствии автокорреляции в исследуемом ряду фактическое значение коэффициента автокорреляции r(1) сопоставляется с табличным (критическим) значением с заданным уровнем значимости. Если фактическое значение коэффициента автокорреляции меньше табличного, то гипотеза об отсутствии автокорреляции в ряду может быть принята, а если фактическое значение больше табличного – делают вывод о наличии автокорреляции во временном ряду.

Соответствие ряда остатков нормальному закону распределения важно с точки зрения правомерности построения доверительных интервалов прогноза. Проверку данной гипотезы можно осуществить с использованием RS-критерия, который вычисляется по формуле

(13.17)

где и соответственно максимальный и минимальный уровни ряда остатков;

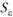– среднеквадратическое отклонение ряда остатков

Если расчетное значение RS попадает между табулированными границами с заданным уровнем вероятности, то гипотеза о нормальном распределении ряда остатков принимается. (Для п = 10 и 5%-ного уровня значимости этот интервал равен 2,7-3,7). В этом случае допустимо строить доверительный интервал прогноза.

Выбранная трендовая модель является адекватной реальному процессу, представленному временным рядом, если все перечисленные гипотезы не отвергаются и, следовательно, ее можно использовать для построения прогнозных оценок. В противном случае – необходимо подбирать другую модель.