Оценка инвестиционной деятельности с учетом соотношения доходности и риска

Очевидно, каждый инвестор желает, чтобы усилия его менеджера привели к формированию такого портфеля, который давал бы отдачу выше, чем нерегулируемые портфели, например рыночный портфель (оцениваемый на основе какого-нибудь рыночного индекса, положим, индекса ММВБ). Строго говоря, добиться подобного результата можно либо путем селекции (пассивного способа управления) – подбора в диверсифицированный портфель ценных бумаг, имеющих лучшее, чем среднерыночное, соотношение риск/доходность, либо путем тайминга (активного способа управления) – постоянной продажи финансовых средств, цена которых снижается, и покупки финансовых средств, растущих в цене, либо обоими путями одновременно. Заметим, что оценка результатов управления портфелем лишь па основе реализованной доходности регулируемого портфеля не вполне корректна, так как при этом не учитывается риск инвестирования в портфель ценных бумаг. Так, если портфель фонда включает в основном ценные бумаги с фиксированным доходом, то доходность такого портфеля заведомо ниже доходности портфеля фонда, оперирующего акциями; следовательно, результаты управления портфелями фондов нельзя оценивать только по достигнутой доходности портфелей.

Все это заставляет найти способы оценки инвестиционной деятельности, которые учитывали бы соотношение доходности и риска портфеля ценных бумаг. Рассмотренные ранее способы определения оптимального портфеля позволяют на основе теории САРМ разработать критерии оценки инвестиционной деятельности и ввести специальные единицы, меры, такой оценки, учитывающие как реализованную доходность, так и риск инвестиций.

При использовании модели САРМ для оценки соотношения доходности и риска портфелей за периоды расчета в прошлом необходимо учитывать, что теория САРМ позволяет объяснять ценообразование финансовых средств с использованием ожидаемых, будущих значений доходности и риска. Иными словами, модель САРМ описывает, каким образом должна устанавливаться цена финансовых средств:

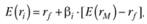
Однако если полученные по САРМ ожидаемые величины доходности не слишком разнятся с реально наблюдаемыми данными и если доходности финансовых средств за прошлый и будущий периоды не имеют значительных разбросов, то основанные на САРМ меры можно использовать для оценки инвестиционной деятельности за прошедший период. Наиболее известными мерами такой оценки служат меры, предложенные Дж. Трейнором (Jack Treynor), М. Дженсеном (Michael Jensen) и У. Шарпом ( William Sharpe).

МераТрейнора

Трейнор предложил ввести специальную единицу, обозначенную им 7), как меру, оценивающую на основе уже наблюдавшихся данных доли реализованной отдачи портфеля на единицу систематического риска. При этом степень систематического риска оценивается коэффициентом "бета" портфеля:

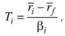
где 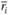– среднее значение наблюдавшихся доходностей портфеля за исследуемый период (в качестве средней величины доходности можно выбирать среднее арифметическое или среднее геометрическое значение); 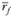– среднее значение наблюдавшихся безрисковых доходностей за исследуемый период; 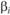– портфельная бета оцениваемого портфеля.

Меру 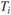любого i-го портфелянеобходимо сравнивать с рыночной мерой 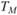, равной 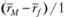, так как коэффициент "бета" рыночного портфеля равен единице. Если для рассматриваемого портфеля 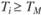, то этот портфель превосходит рыночный и результаты управления портфелем следует признать положительными. Если же 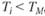, то портфель управлялся неудовлетворительно.

Алгоритм проведение оценки результатов управления портфелем с использованием меры Трейнора следующий.

1. Выбрать промежуток времени в прошлом, за который проводится оценка, и этот промежуток времени разбить на N равных по длительности шагов расчета.

2. С учетом имеющихся данных о стоимости портфеля в начале и в конце каждого шага расчета, а также наблюдавшихся денежных потоков вычислить но одному из рассматриваемых в предыдущем параграфе способу доходности ri,t портфеля за шаги расчета.

3. Выбрать индекс рынка ценных бумаг и на его основе рассчитать доходности 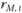рыночного портфеля за эти же шаги расчета.

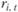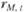4. С использованием величин и рассчитать значение портфельной беты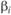для оцениваемого портфеля.

5. Оделить величины безрисковой доходности 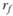за каждый шаг расчета.

6. Найти средние величины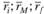

7. Вычислить меры Трейнора 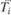для оцениваемого портфеля и 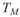для рыночного портфеля, после чего провести их сравнение и сделать соответствующий вывод о качестве управления портфелем.

Представим, что оценивается деятельность трех менеджеров, управляющих портфелями А, В, С за три последних года. На основе имеющихся сведений о ежегодной доходности портфелей вычислим среднюю геометрическую годовую отдачу каждого портфеля 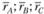. Зная изменения рыночного индекса за этот же промежуток времени, вычислим портфельную бету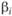каждого портфеля, а также определим средние геометрические годовые значения безрисковой ставки процента 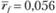и доходности рыночного портфеля 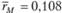(условные данные). Предположим, что получены следующие данные (табл. 5.4).

Таблица 5.4

Данные для вычисления меры Трейнора

Параметры	Портфели			Рыночный
	А	В	С
Средняя доходность	0,124	0,136	0,118	0,108
Коэффициент "бета"	1,120	0,820	1,450	1,000
Мера Трейнора	ТA= 0,060714	ТB=0,097561	ТC= 0,042759	ТM= 0,052

Значения Ti для оцениваемых портфелей вычисляются следующим образом:

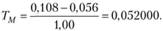
Как следует из табл. 5.4, с точки зрения реализованной доходности, все три портфеля превосходят рыночный портфель. Однако эти доходности надо еще соотнести с уровнем систематического риска (коэффициентом "бета") каждого портфеля. Для портфеля С риск несоизмеримо высок по сравнению со средней реализованной доходностью , поэтому рыночный портфель доминирует над портфелем С.

Использование меры Трейнора можно иллюстрировать также графически (рис. 5.1).

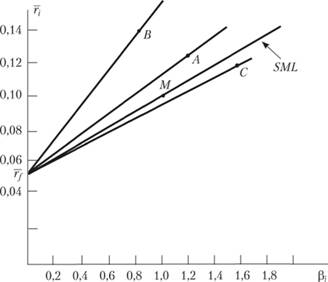
Рис. 5.1. Графическая интерпретация меры Трейнора

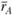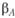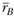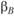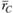Па графикеточки А, В, С и Мсоответствуют средним значениям: и ; и 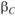; 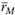и ; и 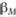. Через эти точки и точку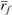проведены линии, которые Трейнор назвал линиями возможных портфелей (portfolio possibility line – PPL). Они показывают, какие композиционные портфели можно сформировать, комбинируя безрисковое ссуживание или заем и портфели А, В, С.

Через точку М проведена линия SML. Обратим внимание на принципиальное отличие SML, построенной для ожидаемых значений 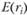, и SML, построенной по результатам фактических, реализованных данных. В первом случае все ценные бумаги и все портфели соответствуют точкам SML, в противном случае они будут неправильно оценены и рыночные механизмы приведут цены к равновесию. Когда же SML строится на основе фактических данных, то портфели и ценные бумаги могут и не лежать на линии SML, как в нашем случае для портфелей А, В и С.

PPL портфеля В доминирует над всеми остальными линиями, поэтому можно утверждать, что менеджер этого фонда добился наилучших результатов за прошедшие три года. Худший результат имеет менеджер портфеля С, поскольку для этого портфеля полученное соотношение риск/доходность ниже рыночного.

Специфический случай возникает, когда портфельная "бета" управляемого портфеля отрицательная (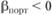). Очевидно, что в этом случае при 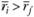мера Трейнора отрицательна 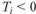, следовательно, она всегда меньше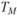. Однако на этом основании нельзя утверждать, что данный управляемый портфель хуже рыночного. Чтобы провести оценку управляемого i юртфеля в случае 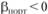, надо поступить следующим образом:

а) найти значение средней доходности портфеля, соответствующее модели САРМ, при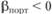

б) сравнить вычисленное ранее значение 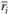и 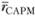. Если 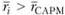, то управляемый портфель лучше рыночного, и результаты управления портфеля можно признать удовлетворительными.