Оценка доходности в случае притоков и оттоков денежных средств
На практике очень часто при оценке реализованной доходности портфеля за оцениваемый промежуток времени необходимо принимать во внимание, что за этот период происходят притоки средств в портфель и отток средств из портфеля. В этом случае оценка доходности требует специальных приемов. При этом следует иметь в виду, что различные методы оценки доходности в подобных случаях могут обеспечивать несовпадающие результаты. Во многом конечные результаты оценки реализованной доходности определяются тем, для кого из участников инвестиционного процесса делаются такие оценки. Чаще встречаются три направления оценки доходности управляемого портфеля.
1. Для инвестора основным является ответ на вопрос: какую фактическую среднюю годовую доходность он получил (или какую ожидаемую доходность он может получить) за счет инвестирования средств в портфель на длительный промежуток времени, когда важно учитывать возможность реинвестирования получаемых от портфеля доходов и начисление сложного процента? Подобные оценки проводят с использованием внутренней нормы доходности IRR.
2. Для портфельного менеджера, который не имел возможности влиять на время и объемы притоков и оттоков средств, важно ответить на вопрос: какую совокупную доходность обеспечил управляемый портфель за оцениваемый промежуток времени? Для таких оценок используется взвешенная во времени доходность.
3. Если портфельный менеджер имеет возможности для выбора момента и объемов вложений и изъятий, и если оценка совокупной доходности проводится за относительно короткий промежуток времени, когда начисление сложного процента не является важным, то используется денежно взвешенная (взвешенная по деньгам) доходность.
Внутренняя норма доходности IRR. Как известно, внутренняя норма доходности IRR – это такая ставка дисконта, при которой приведенная стоимость потоков денег за определенный период равняется начальной инвестиционной сумме (т.е. чистая приведенная стоимость NPV равна нулю). Рассмотрим сначала простой пример.
Пример 5.2. Инвестор 1 марта передал в доверительное управление открытому паевому фонду "Омега" денежные средства в размере 90 тыс. руб. 1 апреля инвестор вкладывает в фонд дополнительные 5 тыс. руб.; после этого подобные же взносы сделаны 1 мая, 1 июня и 1 июля. 31 июля чистые активы фонда, приходящиеся на паи инвестора, составили 116,138 тыс. руб. Какую среднюю доходность обеспечил этот паевой фонд инвестору в расчете за месяц и за год?
Решение
Для ответа необходимо вычислить ежемесячную внутреннюю норму доходности за рассматриваемый период, а затем трансформировать ее в годовую доходность.
В нашем случае расчета IRR надо принимать во внимание следующее:
• начальная инвестиционная сумма составляет 90 тыс. руб.;
• дополнительные вклады в фонд (притоки денег) надо учитывать со знаком "минус", поскольку эти суммы не обусловлены результатами управления активами фонда;
• если бы за период оценки инвестор изъял часть средств из доверительного управления, то такие оттоки денег использовались бы со знаком "плюс";
• конечная сумма 116,138 тыс. руб. учитывается со знаком "плюс".
Следовательно, IRR вычисляется в данном примере по формуле
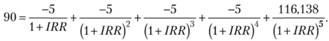
Алгебраически такое уравнение не решается, и вычислить IRR по этой формуле можно либо методом подбора, либо используя специально запрограммированные калькуляторы. В нашем случае IRR = 0,012, или 1,2%. Данная величина представляет величину IRR за месяц, т.е. среднюю ежемесячную доходность. Поскольку доходность обычно указывается за год, то необходимо трансформировать ежемесячную величину IRR в годовое значение. При этом, строго говоря, можно определить арифметическую годовую доходность и геометрическую годовую доходность. Арифметическая годовая доходность подсчитывается путем сложения ежемесячных доходностей. В нашем случае необходимо величину 1,2% умножить на 12 (количество месяцев в году):
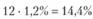– арифметическая годовая доходность 1RR.
Для определения геометрической годовой доходности необходимо величину
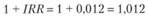
возвести в двенадцатую степень и вычесть единицу:
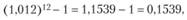
т.е. 15,39% составляют геометрическую годовую доходность IRR.
Заметим, что поскольку геометрическая доходность дает возможность учета сложного процента (процента на процент), то она является более приемлемой для оценки инвестиционной деятельности с использованием IRR.
Как указывалось ранее (см. главу 2), применение IRR предполагает равную длительность шагов, за которые проводится оценка (как это, например, происходило в рассмотренном выше примере). В этой связи более сложной является задача нахождения IRR, когда потоки денег поступают нерегулярно, через разные промежутки времени. И в этом случае необходимо находить внутреннюю норму доходности за одинаковые по длительности шаги расчета. Так, если правилами интервального паевого фонда установлено, что периоды, в течение которых пайщикам предоставляется право на погашение принадлежащих им паев, устанавливаются раз в полгода, то имеет смысл подсчитывать IRR за полгода. Если же одинаковые по длительности шаги расчета выявить не удается (как это может происходить в открытых паевых фондах), то необходимо устанавливать длительность шага расчета в один день, а потом трансформировать дневную внутреннюю норму доходности в ежемесячную и годовую величину.
Пример 5.3. Вернемся к инвестиционному фонду "Вега", рассмотренному в начале параграфа: фонд располагал 120 млн руб. по состоянию на 28 февраля. 7 марта в 9.00 на его счет были переведены дополнительные 30 млн руб. и 31 марта в фонде насчитывалось 152,175 млн руб. Вычислим дневную внутреннюю доходность.
Решение
По условию:
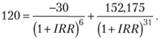
что дает IRR = 0,0005, или 0,05%. В таком случае геометрическая доходность за март находится возведением в 31-ю степень величины 1,0005 за вычетом единицы: (1,0005)31 -1 = (1,01562 – 1), или 1,56%, а арифметическая – умножением 0,0005 на 31: 0,0005 • 031 = 0,155, или 1,55%. Значит, оценивая деятельность менеджера фонда "Вега", мы должны иметь в виду, что величина IRR за март была 1,56%. Тогда годовая величина IRR составит
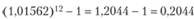, или 20,44%.
Еще раз следует обратить внимание на то, что IRR применяют для оценки результатов управления портфелем с позиции инвестора. Использование IRR в качестве показателя средней доходности портфеля для оценки деятельности портфельного менеджера не корректно, особенно, если решения по вкладам и изъятиям принимает инвестор, а не портфельный менеджер. Рассмотрим следующий пример: 01.01.2008 г. инвесторы А и В передают денежные средства в индивидуальное доверительное управление в сумме 1 млн руб. и дают управляющему указание сформировать индексный портфель. В течение последующих трех лет индекс РЦБ, взятый за основу индексного портфеля, менялся следующим образом (табл. 5.1).
Таблица 5.1
Данные для оценки индексных портфелей
|
Дата |
Величина индекса |
Доходность портфеля по индексу |
|
01.01.2008 |
1000 |
|
|
01.01.2009 |
1100 |
+ 10% |
|
01.01.2010 |
880 |
-20% |
|
01.01.2011 |
1100 |
+25% |
Поскольку за три года индекс вырос с 1000 до 1100 пунктов, то реализованная доходность индексного портфеля за три года составит 10%, что соответствует годовой средней геометрической доходности:
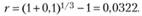
Предположим, что клиенты А и В самостоятельно принимают решение о вложении и снятии денежных сумм. При этом инвесторы поступают по-разному:
• инвестор А: вкладывает дополнительные 500 тыс. руб. 01.01.2009 г. перед падением индекса, а затем снимает 280 тыс. руб. 01.01.2010 г. перед его подъемом;
• инвестор В: снимает 500 тыс. руб. 01.01.2009 г. накануне падения индекса и вкладывает 460 тыс. руб. 01.01.2010 г. перед подъемом индекса.
С учетом доходности индексного портфеля денежные потоки по портфелям инвесторов A и В, а также начальные и конечные стоимости портфелей в каждом году будут принимать следующие значения (табл. 5.2).
Таблица 5.2
Начальные и конечные стоимости портфелей
|
Дата |
Инвестор А, тыс. руб. |
Инвестор В, тыс. руб. |
||||
|
Денежный поток |
Начальное значение |
Конечное значение |
Денежный поток |
Начальное значение |
Конечное значение |
|
|
01.01.2008 |
-1000 |
1000 |
1100 |
-1000 |
1000 |
1100 |
|
01.01.2009 |
-500 |
1600 |
1280 |
+500 |
600 |
480 |
|
01.01.2010 |
+280 |
1000 |
1250 |
-460 |
940 |
1175 |
|
01.01.2011 |
+ 1250 |
- |
- |
+ 1175 |
- |
- |
Как оцепить полученные результаты? Строго говоря, эго можно сделать следующими способами.
1. Выше уже было подсчитано, что и для инвестора А, и для инвестора В доходности их портфелей, измеренные по величинам индекса, идентичны и составляют 3,22% годовых (10% за три года), т. е. портфельный менеджер обеспечил одинаковые результаты для обоих инвесторов.
2. Если полагать, что начальные суммы инвестиций обоих инвесторов составляли 1000 тыс. руб. и через три года стоимость портфеля инвестора А равна 1250 тыс. руб., а инвестора В – 1175 тыс. руб., то за три года портфель инвестора А обеспечивает доходность 25%, а инвестора В – 17,5%. Но такие оценки не учитывают притоки и оттоки денег но портфелям инвесторов, поэтому являются неприемлемыми.
3. С учетом возникающих притоков и оттоков денег результаты инвестирования для инвесторов следует оценивать с использованием IRR:
• для инвестора А:
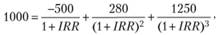
откуда IRR = 0,008, или 0,8%;
• для инвестора В:
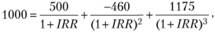
откуда IRR = 0,0806, или 8,06%.
Таким образом, грамотное управление инвестором В своим портфелем обеспечивает ему среднюю годовую доходность, измеренную как внутренняя норма доходности IRR, в 10 раз выше, чем доходность портфеля инвестора А.
4. Очевидно, что использование IRR для оценки работы менеджера в тех случаях, когда он не в состоянии влиять на притоки и оттоки денег, некорректно: исходя из величин IRR, портфель инвестора В управлялся значительно лучше, хотя, как уже указывалось, измеренная по индексу доходность обоих портфелей одинакова.