Оценка доходности и риска портфеля

Доходность портфеля напрямую зависит от ожидаемых доходностей входящих в него активов и удельного веса (доли) каждого из них в его структуре. Таким образом, это просто средняя взвешенная величина из соответствующих доходностей отдельных активов. Рассмотрим следующий пример.

Пример 12. Пусть портфель сформирован из двух рисковых активов (например акций) А и В, характеристики которых представлены в табл. 8.2. Требуется определить доходность и риск портфеля АВ.

Таблица 8.2

Рисковые активы портфеля

Состав	Доходность, %	Риск, %	Доля в портфеле
Актив А	5	20	2/3
Актив В	15	40	1/3

Решение

Доходность данного портфеля может быть определена по формуле

где ХA, ХB – доля соответствующего актива в портфеле; RA, RB – средняя ожидаемая доходность активов A и В.

Для рассматриваемого примера средняя ожидаемая доходность портфеля будет равна

Под риском можно понимать вероятность возникновения каких-либо отклонений от ожидаемого события. Основополагающими мерами риска финансового актива являются такие показатели, как стандартное отклонение (σ) и дисперсия (D = σ2) сто доходности. В качестве синонима понятия "стандартное отклонение" используют также термин "волатильность". Стандартное отклонение и дисперсия доходности актива отражают степень возможного разброса его фактической доходности вокруг его средней (наиболее вероятной) доходности. Данные меры риска можно определить на основе прошлых данных статистики доходности актива.

Доходность актива на рассматриваемом интервале определяется следующим образом:

где St-1 – стоимость актива в начале интервала наблюдения; St – стоимость актива в конце интервала наблюдения.

Пусть имеются значения доходности акции за п равных интервалов наблюдения. За первый интервал она составила величину R1, за второй – R2 и т.д., за п-й интервал – Rn

Средняя доходность актива за наблюдаемый период (R) рассчитывается по формуле

Дисперсия доходности актива определяется как мера разброса наблюдаемой доходности (в процентах) от ее математического ожидания (средней величины). Формула генеральной дисперсии имеет вид

В случае если количество наблюдений незначительно (меньше 30), то для получения несмещенной оценки рекомендуется использовать так называемую исправленную дисперсию:

Показателем, характеризующим относительный уровень риска финансового актива, является стандартное отклонение его доходности от ожидаемой (средней за период):

При этом оценка допустимого уровня стандартного отклонения является субъективной и характеризует готовность инвестора принимать риск с учетом возможной доходности финансового актива.

Для количественной оценки риска используют коэффициент вариации, отражающий меру относительного разброса случайной величины; он показывает, какую долю среднего значения этой величины составляет ее средний разброс:

Как и для отдельного актива, риск портфеля измеряется показателями, характеризующими изменчивость его доходности, например дисперсией D или стандартным отклонением σ.

Однако помимо индивидуальных рисков отдельных активов и доли каждого из них в структуре портфеля на его совокупный риск значительное влияние будет также оказывать степень зависимости доходности включенных активов друг от друга. Поэтому расчет риска портфеля как среднего взвешенного из рисков составляющих его активов будет некорректным, так как приведет к игнорированию возможных взаимосвязей между изменениями их доходности.

Для оценки взаимосвязи изменений двух переменных в теории вероятностей и математической статистике используются два показателя: ковариация и корреляция.

Ковариация характеризует взаимную изменчивость двух показателей.

Формула для определения ковариации доходностей двух активов А и В будет иметь следующий вид:

где п – количество интервалов, за которые наблюдались значения доходности.

Положительная ковариация означает, что доходности двух активов изменяются в среднем в одном направлении, а отрицательная – что в противоположном.

Понятие корреляции двух показателей аналогично понятию их ковариации. Коэффициент корреляции является производным показателем от ковариации и вычисляется делением (нормированием) последнего на произведение соответствующих стандартных отклонений:

Коэффициент корреляции принимает значение в фиксированном диапазоне [-1; +1] и поэтому более удобен и нагляден в интерпретации.

При этом значение corr = +1 (полная положительная корреляция) означает существование линейной зависимости между изменениями двух показателей. Нетрудно заметить, что доходность любого актива полностью положительно коррелированна сама с собой.

При corr = -1 (полная отрицательная корреляция) между изменениями показателей существует обратная линейная взаимосвязь.

Если corr = 0 (отсутствие корреляции), показатели изменяются независимо друг от друга.

Понятия ковариации и корреляции играют важнейшую роль в определении риска портфеля и теории инвестиций в целом. В частности, с учетом возможных взаимосвязей доходностей риск портфеля из двух активов А и В может быть определен по формуле

где ХA, ХB – доли соответствующих ценных бумаг (A и В) в портфеле; σA, σB – стандартные отклонения доходностей ценных бумаг (A и В); covAB – коэффициент ковариации доходностей ценных бумаг (A и В).

Через коэффициент корреляции риск портфеля из двух активов А и В может быть определен по формуле

где ХA, ХB – доли соответствующих ценных бумаг (A и В) в портфеле; σА, σΒ – стандартные отклонения доходностей ценных бумаг (А и В); corrАВ – коэффициент корреляции доходностей ценных бумаг (Л и В).

Определим риск портфеля AВ из примера 11:

Как следует из полученного результата, риск портфеля непосредственно зависит от значения коэффициента ковариации (а следовательно, и корреляции). Однако последний никак не влияет на сто доходность. Рассмотрим три важных частных случая, используя данные рассмотренного примера.

1. При corr = 1 (полная положительная корреляция) риск портфеля из двух активов будет равен

Таким образом, в данном случае риск портфеля зависит только от риска и доли каждого актива, входящего в портфель.

В частности, для примера 11 риск портфеля будет равен

На рис. 8.5 приведена графическая интерпретация взаимосвязи риска и доходности портфеля из двух полностью коррелированных активов. Точкой АВ на графике обозначено местоположение портфеля из нашего примера.

Как и следовало ожидать, зависимость является линейной. Таким образом, при corrAВ = 1 все возможные портфели, построенные из различных комбинаций активов A и В, будут лежать на одной прямой, проведенной между точками их расположения. Для нашего примера это будет прямая, проходящая через точки А и В с координатами (20%; 5%) и (40%; 15%) соответственно.

2. При corr = 0 (независимость изменения доходностей активов) риск портфеля из двух активов равен

Рис. 8.5. Доходность и риск портфеля AВ при corrAB = 1

Для примера 11 риск портфеля при corrAB = 0 будет равен

На рис. 8.6 приведена графическая иллюстрация для данного случая. Нетрудно заметить, что риск портфеля А В меньше, чем индивидуальные риски составляющих его активов.

3. При corr = –1 (полная отрицательная корреляция) риск портфеля из двух активов будет равен

Таким образом, в данном случае риски отдельных активов в портфеле уравновешивают друг друга. Более того, при оп-

Рис. 8.6. Доходность и риск портфеля АВ при corrAB = 0

Рис. 8.7. Доходность и риск портфеля AВ при corrAB = -1

ределенной структуре портфеля его риск может быть полностью устранен.

В частности, для примера 11 риск портфеля будет равен

На рис. 8.7 приведена графическая иллюстрация данного случая.

Для определения структуры портфеля, приводящей к полному устранению риска, выразим долю актива B через актив A. Поскольку общая сумма долей каждого актива в портфеле должна быть равна 1, или 100%, имеем: ХB = (1 – ХА). Подставив полученное выражение в предыдущую формулу с условием σAΒ = 0, получим

Для рассматриваемого портфеля доля актива А составит 0,4/(0,2 + 0,4) = 0,667 (или 2/3). Доля второго актива B будет равна (1 – 0,667) = 0,333 (или 1/3), что и соответствует условиям примера.

На практике доходности активов, как правило, имеют положительную корреляцию. В общем случае (при 0 < corr < 1) доля инвестиций в актив A, которая минимизирует риск портфеля из двух активов, определяется по формуле

где через обозначена корреляция доходностей активов A и В.

Соответственно,

Полученные результаты позволяют сделать ряд важных выводов.

1. При отсутствии полной положительной корреляции между доходностями активов () риск сформированного из них портфеля будет всегда меньше средней взвешенной рисков отдельных активов.

2. В случае полной отрицательной корреляции между доходностями активов () риск сформированного из них портфеля может быть сведен к нулю.

3. Если доходности активов сильно коррелированы между собой (), формирование портфеля не приводит к снижению риска.

Снижение инвестиционного риска в результате формирования портфеля из различных активов известно как эффект диверсификации.

Полученные результаты могут быть обобщены для произвольного количества рисковых активов. Формула для определения ожидаемой доходности портфеля, состоящего из п активов, имеет вид

Формула для определения ожидаемого стандартного отклонения доходности портфеля, состоящего из п активов, имеет вид

В формуле стоит знак двойной суммы . Это означает, что, раскрывая его, мы должны вначале взять значение i= 1 и умножить на него все значения j от 1 до п. Затем повторить данную операцию, но уже для i = 2, и т.д. В итоге получим п2 слагаемых.

Для оценки риска портфеля, состоящего из нескольких активов, можно использовать аппарат матриц.

Уровень риска портфеля ценных бумаг (через дисперсию) будет оцениваться следующим образом:

где X – матрица-столбец удельных весов активов в портфеле:

XT – транспонированная матрица удельных весов активов в портфеле (матрица-строка):

Q – матрица ковариаций доходностей активов в портфеле:

Таким образом, оценка риска портфеля ценных бумаг (по дисперсии) осуществляется путем умножения матриц:

Риск портфеля определяется по формуле . Также формула для оценки риска портфеля может быть представлена через корреляцию доходностей ценных бумаг:

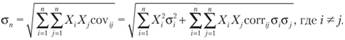
Данная формула наглядно показывает, что портфельный риск состоит из двух различных компонент, или слагаемых. Первое слагаемое – это риск, связанный только с изменчивостью (дисперсиями) доходностей отдельных активов. Этот риск называется несистематическим или уникальным риском, присущим отдельным активам или предприятиям. Примерами несистематических рисков могут служить:

• утрата активов, ключевых поставщиков и клиентов, персонала и т.п.;

• падение спроса или цен на продукцию предприятия;

• неудачная реализация новых проектов;

• неэффективный менеджмент;

• судебные разбирательства, забастовки и т.п.

Второе слагаемое в указанной формуле определяет риск, связанный с взаимосвязью (корреляцией или ковариацией) между взаимными изменениями доходностей активов, включенных в портфель. Данному риску в большей или меньшей степени подвержены все хозяйствующие субъекты. Поэтому его называют систематическим или рыночным. Основными причинами этого риска могут быть:

• спад или кризис в экономике страны;

• политическая нестабильность;

• резкие изменения в законодательстве, финансовой (налоговой, денежной, бюджетной и т.п.) политике государства;

• инфляция, колебания процентных ставок и др.

Необходимость разделения риска на несистематический и систематический заключается в том, что эти виды риска ведут себя по-разному, когда количество активов, включаемых в портфель, увеличивается.

Предположим, что все активы в портфеле независимы между собой (все corrij = 0) и имеют одинаковые веса (Xi = 1/п). Тогда формула оценки риска портфеля активов примет следующий вид:

Выражение под корнем является суммарным собственным риском активов, образующих портфель. Однако собственный риск портфеля будет в п раз меньше. Очевидно, что с ростом числа независимых активов в портфеле его собственный риск будет снижаться и в конечном итоге станет несущественным.

Пусть теперь портфель состоит из п активов, взятых в равных долях (Xi = 1/п), имеющих одинаковые положительные корреляции и дисперсии (т.е. все 0 < corrij = const < 1 и σ1 = σ2 = ... = σn = σ = const). Формула в этом случае примет следующий вид:

При первое слагаемое в данной формуле будет

стремиться к 0, а второе – к величине .

Таким образом, несмотря на диверсификацию, минимальный риск такого портфеля остается равным . Это свидетельствует о том, что для портфеля из положительно коррелированных активов () существует некоторый предел диверсификации, и в данном случае полностью устранить риски невозможно.

Из вышеизложенного можно сделать следующие выводы:

• если доходности активов не являются полностью положительно коррелированными (), то диверсификация портфеля уменьшает его дисперсию (риск) без уменьшения его средней доходности;

• в случае хорошо диверсифицированного портфеля несистематическим риском можно пренебречь, так как он стремится к нулю;

• диверсификация не ведет к устранению систематического риска.

Графическая иллюстрация эффекта диверсификации, а также ее влияние на различные виды риска приведены на рис. 8.8.

Рис. 8.8. Эффект диверсификации 8.4.2. Теория Марковица

Основы теоретического подхода к анализу и формированию инвестиционного портфеля из рисковых активов, базирующегося на идее диверсификации, были разработаны американским ученым Г. Марковицем (G. Markowitz), которому впоследствии была присуждена Нобелевская премия в области экономики.

Портфельная теория Марковица базируется на ряде допущений, наиболее существенными из которых являются следующие.

1. Инвесторы производят оценку инвестиционных портфелей, основываясь на ожидаемых доходностях и их стандартных отклонениях или дисперсиях за период владения.

2. Инвесторы никогда не бывают пресыщенными. При выборе между портфелями они предпочтут тот, который при прочих равных условиях дает наибольшую ожидаемую доходность.

3. Инвесторы не расположены к риску. Таким образом, при выборе между портфелями они предпочтут тот, который при прочих равных условиях имеет меньший риск (стандартное отклонение).

Из выполнения пунктов 2 и 3, в частности, следует, что все инвесторы ведут себя рационально. Тогда эффективный с точки зрения критерия "риск – доходность" портфель будет выбираться рациональным инвестором из всего множества доступных активов и их комбинаций (портфелей), обеспечивающих:

• максимальную ожидаемую доходность R для некоторого уровня риска σ;

• минимальный риск σ для заданного уровня ожидаемой доходности R.

Набор портфелей, удовлетворяющий этим условиям, называется эффективным множеством портфелей. Множество всех эффективных портфелей в системе координат "риск- доходность" образует так называемую эффективную границу, или границу Марковица. Графическая иллюстрация доступного и эффективного множества портфелей представлена на рис. 8.9.

Рис. 8.9. Множество доступных портфелей и эффективная граница

Как следует из рисунка и сформулированных выше условий эффективности, привлекательными для рациональных инвесторов будут только те портфели, которые лежат на границе плоскости между точками Е (портфель с наименьшим уровнем риска) и Z (портфель с наибольшим уровнем доходности). Этот участок образует эффективную границу Марковица. Портфели, лежащие ниже точки Е и за точкой Z, а также в любой точке плоскости допустимого множества, не являются эффективными. Рассмотрим в качестве примера портфель N. Как следует из рис. 8.9, этот портфель не может быть эффективным по критерию "риск – доходность", поскольку портфель E1 обеспечивает ту же доходность, но при значительно меньшем уровне риска, а портфель Е2 дает возможность получить бо́льшую доходность при том же уровне риска.

Какой именно портфель выберет инвестор, зависит от его индивидуального отношения к риску. Однако в соответствии с заданными допущениями рациональный инвестор всегда будет выбирать портфель, лежащий на эффективной границе. Этот выбор осуществляется посредством анализа и определения приемлемого соотношения риска и доходности для каждого инвестора.

Задача определения оптимального портфеля для конкретного инвестора может быть решена аналитически – минимизацией риска, выраженного дисперсией или стандартным отклонением при заданном уровне доходности, либо максимизацией доходности при заданном уровне риска. В классической постановке Марковица задача формирования оптимального портфеля имеет следующий вид:

при условиях

Данная задача решается методами квадратичного программирования. Решение этой задачи требует предварительной оценки N доходностей, N дисперсий и ковариаций, т.е. параметров (например, анализ 20 рисковых бумаг потребует оценки 230 параметров). Следует отметить, что в настоящее время с вычислительной точки зрения провести подобную оценку не составляет большого труда, в частности для этих целей можно использовать специальные средства популярного офисного пакета MS Excel.

Подходу Марковица присущи и другие ограничения, связанные с положенными в его основу допущениями. Вместе с тем полученные им результаты положили начало современной теории портфельного инвестирования, дали мощный толчок к дальнейшим исследованиям и в целом сохраняют свою актуальность по нынешний день.