Отношения между понятиями
Понятия, связь между которыми по содержанию является весьма далекой, называются несравнимыми ("безответственность" — "кирпич", "счастье" — "гипотенуза"). Конечно же, сравнивать можно что угодно, например: "Эх, жизнь моя жестянка, а ну ее в болото!" Или, как говорил Козьма Прутков, болтун подобен маятнику: того и другого мало остановить. Возможны самые неожиданные сожаления и уподобления, но с формально-логической точки зрения понятия несовместимы, если у них нет общих существенных признаков.
Понятия, с помощью которых отражаются предметы, имеющие общие существенные признаки, называются сравнимыми. Сравнимые понятия бывают несовместимые и совместимые (рис. 2.3).
Несовместимые понятия — такие, в которых имеются исключающие друг друга признаки. Их объемы не совпадают ни в одном элементе. Например, "студент" — "школьник". Действительно, нет ни одного студента, который в то же время был бы школьником и наоборот.
Совместимые понятия — такие, в которых нет признаков, исключающих друг друга. Их объемы частично или полностью совпадают ("студент" — "отличник").
• Совместимые понятия находятся в следующих отношениях:
Равнозначность (тождество) — отношение понятий, в которых мыслится один и тот же предмет, т.е. объемы понятий полностью совпадают. Например: "агент", "брокер", "дилер", "комиссионер", "маклер". Все эти понятия обозначают юридическое или физическое лицо, совершающее определенные действия по поручению другого лица (принципала) за его счет и от его имени, а также действия в подготовке сделок, но без права их подписи.
Для наглядности отношения между понятиями (а также между суждениями) выражаются геометрическим методом, графически. В истории логики применялись различные способы графики. Так немецкий философ, астроном, математик И. Г. Ламберт (1728—1777) применял графические линии ("ламбертовы линии"). Графику использовал чешский математик и логик Б. Больцано (1781—1848). Отношения между классами он изображал с помощью прямоугольных диаграмм. Но особенно успешно оперировал графическим аппаратом диаграмм английский логик, профессор, член Королевского общества Дж. Венн (1834— 1923). Разработанный им метод весьма наглядно отражал логику взаимосвязи понятий и поэтому имел не только иллюстративное, но и эвристическое значение.
Диаграммы Дж. Венна широко используется в наши дни. Однако наибольшее распространение получил метод круговых схем, который предложил математик, физик, астроном, член Петербургской академии наук Л. Эйлер (1707—1783).
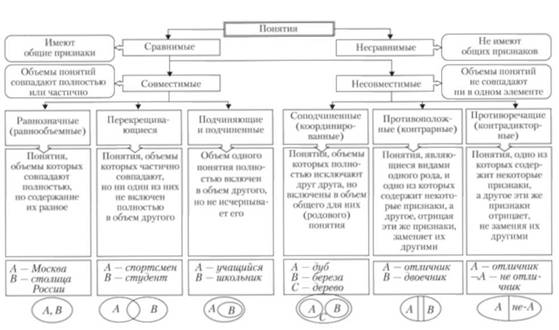
Рис. 2.3. Отношения между понятиями
Каждый круг охватывает объем понятия, а сами понятия символически обозначаются буквами. Так, приведенный пример равнозначности понятий графически выглядит следующим образом:

Пересечение (перекрещивание) — такое отношение, которое характеризует частичное совпадение объемов понятий, но при этом ни одно из них не входит полностью в объем другого.

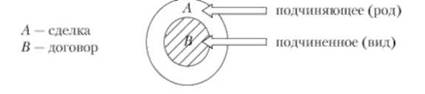
Подчинение (субординация) — такое отношение, когда объем одного понятия полностью входит в объем другого. При этом более широкое по объему понятие является подчиняющим (родовым), а менее широкое по объему — подчиненным (видовым). Родовидовые отношения лежат в основе многих логических операций с понятиями (обобщение, ограничение, определение и деление).
• Несовместимые понятия имеют также три вида отношений.
Соподчинение (координация) — такое отношение, которое свидетельствует, что в родовое понятие входит не одно, а два или более однопорядковых видовых понятий.

Противоположность (контрарность) — такое отношение, в котором находятся понятия, одно из которых содержит некоторые признаки, а другое эти признаки отрицает, замещая их исключающими признаками. Другими словами, объемы противоположных понятий разделены объемом некоторого третьего понятия. Слова, выражающие противоположные понятия, называются антонимами ("черный" — "белый"). Сумма объемов противоположных понятий не исчерпывает объема родового понятия. Между понятиями "черный" и "белый" может быть понятие, отражающее любой другой цвет: зеленый, красный и т.д.

Противоречие (контрадикторность) — такое отношение, в котором находятся понятия, одно из которых содержит некоторые признаки, а другое отрицает эти же признаки, не замещая их никакими другими признаками. Объемы двух противоречащих понятий составляют в сумме весь объем рода, видами которого они являются.

Знание разновидностей понятий, а также отношений между ними служит основой для уяснения операций с понятиями, для изучения других форм мышления.