.6. Особенности прогнозирования параметров полей концентрации в наиболее типичных ситуациях

С учетом изложенных выше соображений и в предположении о совпадении направления ветра с осью X, координат источника залпового выброса – с точкой , а его времени – с моментом t= О, математическая модель поля концентрации принимает вид, аналогичный приведенным ранее выражениям (14.27) и (14.28):

(14.45)

Однако его три функции не совпадают с соотношениями (14.28), так как здесь они уже следующие:

(14.46)

Этот довольно общий результат позволяет применить модель мгновенного выброса для прогноза полей концентрации в других практи-

чески важных ситуациях. Последовательно проиллюстрируем подобную возможность на примере учета особенностей вначале геометрии источника вредного выброса, а затем и динамики его "работы"; причем сделаем это двумя способами – точным и приближенным, начиная с первого.

Для поиска точного решения предположим вначале, что источник представляет собой не точку, а расположенный вдоль оси X отрезок прямой, начало и конец которого соответствуют координатам , при , а интенсивность q выброса из него вредного вещества неизменна во времени, т.е. , В данном случае модель концентрационного поля уже выражается формулой [10]

, первая функция-сомножитель которой есть определенный интеграл от функции :

(14.47)

где Ф(*) – функция Лапласа, описывающая стандартную нормально распределенную случайную величину и называемая эрфик-функцией (см. табл. Г.4 приложения).

Аналогичным образом получается математическая модель поля концентрации при условии, что источник представляет собой уже плоскость, образуемую семейством отрезков прямых, перпендикулярных осиХ В этом случае интегрированию подвергаются две функции и 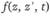, в результате чего можно получить следующие выражения:

(14.48)

Подобным способом могут быть получены точные аналитические модели полей концентрации , формируемых источником вредных выбросов в форме объема или поверхности любой конфигурации. Для этого данный источник нужно представлять множеством точек с равномерной объемной или поверхностной плотностью эмиссии вещества. Некоторые из таких уравнений, полученных из фундаментального решения (14.35), можно найти в работе [10].

Демонстрацию второй возможности приближенного учета специфических особенностей геометрии источника вредных выбросов проведем заменой его пространственных конфигураций на точечные. Достигнуть этого можно одновременным переносом модифицированного подобным образом источника в точку, расположенную левее и сбоку относительно центра, при условии что движение несущей среды совпадает с осью X.

Проиллюстрируем суть подобной "подмены" на примере источника в форме трехмерного параллелепипеда с ортогональными координатным осям гранями длиной и центром в точке По своей сути данная задача в этом случае сводится к нахождению такого расположения фиктивного источника на линии, проходящей через центр этого параллелепипеда и параллельно оси X, которое обеспечит эквивалентное реальному источнику пятно загрязнения в вертикальной плоскости прих = 0. Иначе говоря, струя от точечного источника в сечении х = должна иметь ширину, равную 2L_y.

Оказывается, что достигнуть искомого положения можно тремя перемещениями модифицированного источника во всех трех плоскостях, направление и величина каждого из которых – – определяются следующими уравнениями:

(14.49)

Это означает, что для перехода от модели точечного источника к его модели в виде параллелепипеда можно использовать соотношения (14.45) и (14.46), при условии замены имеющихся там стандартных отклонений на следующие более адекватные такой подмене величины:

Что касается демонстрации последней (из заявленных ранее) особенности – возможности учета разной динамики работы источника вредных выбросов, то и эта задача может быть решена модификацией выбранной выше базовой модели. В частности, поле концентрации , формируемое кратковременными импульсными выбросами постоянной интенсивности, легко построить с помощью выражения (14.45), при условии что в момент времени t' вносится единичная масса вредного вещества, т.е. М = 1.

Если же эпизодические выбросы наблюдаются в течение интервала (0; Т), то при построении концентрационного поля нужно пользоваться двумя аналитическими выражениями: для периода его кратковременной "подпитки" вредным веществом и после этого периода . Данное обстоятельство накладывает дополнительные ограничения, что будет продемонстрировано ниже (см. параграф 15.4) при прогнозе полученных людьми токсодоз.

На этом завершим иллюстрацию конструктивности применения гауссовых моделей для оперативного оценивания полей концентрации вредного вещества и выдадим ряд обобщенных рекомендаций, касающихся наиболее предпочтительного практического применения не только различных способов оценки самых значимых параметров и , но и оперирующих ими моделей (14.27), (14.28) и (14.22) –(14.26).

1. Для повышения точности прогнозирования в режиме реального времени целесообразно использовать обе зависимости и , отдавая предпочтение:

а) формуле (14.32) – для оценки дисперсии , т.е. в направлении, перпендикулярном скорости ветра и параллельном подстилающей поверхности;

б) выражению (14.33) – для дисперсии в вертикальном направлении

2. Наибольшая достоверность при применении этих формул достигается на удалениях от источника выброса в пределах от 0,1 до 10 км, а при расстояниях, меньших 100 м, следует интерполировать значения , используя их линейную зависимость от

3. Для приближенных расчетов можно использовать упрощенные зависимости типа (14.41), а для особо точных – имеющиеся в работе [10] более строгие выражения для стандартных отклонений, учитывающие поправки на время осреднения.

4. Определение коэффициентов турбулентного обмена по громоздким формулам (14.36) – (14.40) нужно совмещать с процедурой численного моделирования системы (14.18) – (14.22) или находить приближенные значения с помощью – путем пересчета по соотношению для

5. Применение гауссовых моделей (14.27), (14.28) и основанной на них компьютерной программы "Токси-2" из комплекса "Токси + Risk" обеспечивает приемлемую точность лишь для прогноза параметров распространения в атмосфере сравнительно легких вредных веществ.

6. Для аварийных и непрерывных вредных выбросов аэрозолей, а также вредных газообразных веществ с плотностью, равной и превышающей атмосферную, более достоверные результаты дают модели типа (14.22) – (14.26) и программа "Токси-3", имеющаяся в упомянутом выше автоматизированном комплексе.

На этом ограничимся в рассмотрении способов определения параметров рассеяния и в установившемся режиме и обратим внимание на особенности оценки нестационарного поля концентрации. Оказывается, что в данной ситуации может быть использован опыт, накопленный при построении полей концентрации газо- и мелкодисперсных выбросов из непрерывно действующего их точечного источника на ОПО при условии модификации рассмотренных выше дисперсионных зависимостей. Легче всего это сделать, заменив в формулах (14.32), (14.33) аргумент на и вдвое уменьшив дисперсию .

Отметим также те недостатки моделей типа (14.27), (14.28) и (14.45), (14.46), которые обусловлены игнорированием следующих факторов:

а) влияния на параметры несущей среды продуктов мощного мгновенного выброса, характеризуемого высокой плотностью и скоростью вредного вещества;

б) наличия в атмосфере слоев с разной температурой и плотностью, сильно меняющих интенсивность диффузионного обмена с продуктами выброса.

Вот почему рассмотренные здесь параметрические модели целесообразно использовать лишь при соблюдении условий, которые будут обсуждены ниже (см. параграф 15.2). В противном случае можно получить необоснованно завышенные или заниженные прогнозы . Последнее будет иметь место, например, из-за раздвоения облака паров сжиженного тяжелого газа под воздействием мощных нисходящих потоков в центре его большого пролива и таких же, но уже – в обратном направлении и по периметру зоны его испарения. Дело в том, что подобные явления можно учесть лишь с помощью моделей (14.18) – (14.21) и программных комплексов численного моделирования типа PHOENIX.

Завершая же параграф и главу в целом, подчеркнем как бы подготовительный характер изложенного в ней материала, что обусловлено спецификой исследуемых до сих пор (начальных) этапов причинения техногенного ущерба. Вот почему примеры, иллюстрирующие работоспособность рассмотренных здесь моделей, а также методов прогнозирования параметров трансформации и разрушительного воздействия продуктов выброса, целесообразно привести после ознакомления со всеми этапами всего процесса, что и будет сделано в последней главе этого раздела данной монографии.