Лекция 3. ОСНОВЫ СХЕМОТЕХНИКИ ЦИФРОВЫХ УСТРОЙСТВ

В результате изучения главы 3 студент должен:

знать

• арифметические и логические основы построения цифровой полупроводниковой электроники;

• основные виды комбинационных цифровых устройств;

• основные виды последовательностных цифровых устройств;

уметь

• разрабатывать принципиальные электрические схемы простейших цифровых устройств;

• выполнять анализ работы простейших цифровых устройств, синтезированных из элементарных логических элементов;

владеть

• методами синтеза цифровых электронных устройств с использованием булевой алгебры и карт Карно.

Двоичная система счисления

В отличие от аналоговых устройств, в которых информационный сигнал может принимать любые значения в некотором диапазоне, в цифровых устройствах носителем информации является цифровой двоичный код. Этот код состоит из множества двоичных разрядов, каждый из которых принимает только два фиксированных значения – "0" или "1". Двум двоичным цифрам соответствуют два состояния электронной схемы. Обычно это два фиксированных уровня напряжения, которые может принимать сигнал на выходе схемы. Поэтому все разнообразие математических операций, выполняемых цифровыми устройствами, основывается на двоичной системе счисления.

Напомним суть записи числа, означающего, например, количество "тысяча триста восемь" в десятичной системе счисления:

По сути, набор цифр "один–три–нуль–восемь" представляет собой код, т.е. перечень коэффициентов (множителей), стоящих перед числом десять (основанием системы счисления) в степени (справа налево): нуль, один, два, три и т.д. "Вес" каждого коэффициента (цифры) определяется разрядом – позицией, которую он занимает в коде (единицы, десятки, сотни, тысячи и т.д.). Поэтому такая система счисления называется позиционной.

В позиционной двоичной системе счисления основанием служит число два, а коэффициентами могут быть только две цифры – нуль (0) и единица (1), поэтому, например, количество "тринадцать" запишется кодом 1101:

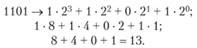
Арифметические действия в двоичной системе выполняют аналогично десятичной.

Рассмотрим сущность выполнения действия сложения, например, чисел 45 и 87 в десятичной системе. Сначала складываем цифры младшего разряда – нулевого, соответствующего 100 – единицам: 5 + 7 = 12. В числе 12 уже две цифры, причем цифра младшего разряда суммы – 2, а цифра 1 принадлежит более старшему разряду – первому, соответствующего 101 – десяткам. Поэтому 2 записываем, 1 – запоминаем, т.е. в младшем разряде суммы, соответствующем единицам, будет 2, а 1, соответствующую более старшему разряду – десяткам, будем учитывать при сложении цифр первого разряда. Далее складываем цифры первого разряда 4 + 8 и прибавляем к ним 1, которую запомнили; получаем 13. Теперь цифра, соответствующая первому разряду суммы – 3, а 1 переносится в старший разряд, соответствующий второму разряду суммы – 102, т.е. сотням.

Аналогично выполняется сложение в двоичной системе, например, чисел "шесть" и "семь" (табл. 3.1). Числа шесть и семь в двоичной системе имеют вид:

Сложение начинаем с нулевого разряда, соответствующего 20:

0 + 1 = 1 (младшая цифра суммы равна 1).

Переходим к сложению цифр первого разряда, соответствующего 21: 1 + 1 = 2. Для записи числа 2 в двоичной системе требуется код: 10 (1 -21 + 0 • 20 = 2), т.е. цифра первого разряда суммы равна 0, а 1 переносим в старший разряд (нуль записываем, один запоминаем). Таким образом, если сумма цифр больше единицы, происходит перенос в старший разряд.

Далее складываем 1 + 1 и прибавляем 1, которую запомнили, получаем 3. Число 3 в двоичной системе записываем кодом 11 (1 • 21 + 1 – 20 = 3), т.е. цифра второго разряда суммы равна 1, а старшая 1 переносится в следующий (третий) разряд.

Таким образом, сумма чисел 110 и 111 равна 1101. Нетрудно убедиться, что это двоичное число – 13 (1 • 23 + + 1 • 22 + 0 • 21 + 1 • 20= 13).

Таблица 3.1

Сложение		Вычитание
десятичная	двоичная	десятичная	двоичная

Примечание: 1^ – перенос из младшего разряда в старший: М – перенос из старшего разряда в младший; • – заем из старшего разряда.

Рассмотрим теперь сущность действия вычитания в десятичной системе на примере: 132 – 87:

• сначала вычитаем цифры нулевого разряда, но так как из двух нельзя вычесть семь, занимаем 1 (один десяток – основание системы счисления) в старшем разряде, что отмечаем точкой над цифрой 3; получаем 10 + 2 = 12; 12 – 7 = 5;

• при вычитании цифр первого разряда необходимо занять 1 в следующем старшем разряде и, учитывая, что в первом разряде осталась цифра 2, получаем 10 + 2 – 8 = 4.

Аналогично выполняем вычитание из числа 1101 (13) числа 110 (6) в двоичной системе:

• нулевой (20) разряд: 1-0=1;

• первый (21) разряд: из нуля нельзя вычесть единицу, поэтому занимаем 1 (т.е. одно основание системы счисления, равное двум) и получаем 2-1 = 1;

• второй (22) разряд: из нуля, оставшегося после занимания единицы в этом разряде, нельзя вычесть единицу, поэтому занимаем 1 (основание, равное двум) в третьем (23) разряде: 2-1 = 1. Получим 111, т.е. двоичное число "семь".

Покажем, что операцию вычитания можно заменить сложением, но для этого уменьшаемое (т.е. 1101) надо складывать с обратным кодом вычитаемого, который получаем, заменив цифры на обратные (т.е. 1 на 0, а 0 на 1). Произведя сложение, переносим 1 из старшего разряда в младший, как показано стрелкой, и получаем двоичный код 111, соответствующий числу "семь".

Действия умножения и деления (а как доказано в математике, и любые другие операции) можно свести к сложению и вычитанию кодов, сдвинутых влево или вправо на то или иное число разрядов. Сдвиг числа влево на один разряд соответствует умножению сто на 2, а вправо – делению на 2. Действительно, каждая цифра числа при его сдвиге влево будет иметь вес уже не i-го разряда, т.е. 2i, а (i + 1)-го, т.е. 2i+1. При сдвиге вправо вес каждой цифры будет уменьшаться в 2 раза, т.е. составит не 2i, а 2i-1.

Покажем, как с помощью операций сложения и сдвига можно выполнить умножение двоичных чисел. Вычисление произведения осуществляют от старших разрядов множителя к младшим но шагам. На каждом шаге анализируют очередную цифру множителя. Если она равна 1, то к промежуточному результату вычислений прибавляют множимое, если 0, то результат оставляют без изменений. При переходе к более младшему разряду промежуточный результат сдвигают влево на один разряд, т.е. умножают на 2 . Последнему шагу вычислений соответствует нулевой разряд множителя. Обозначим через А множимое, через В – множитель, а через bi – i-й разряд множителя. Тогда в результате вычислений но описанному выше алгоритму будет получено число П:

Выражение в последних скобках есть не что иное, как число В, а число П – произведение А и В.

Поскольку вычитание сводится к сложению обратного кода, становится понятным, почему любые математические операции можно осуществить с помощью простейших операций сложения и сдвига, что и используется в процессорах ЭВМ.

Таким образом, если в десятичной системе для записи кодов используется десять цифр (от 0 до 9), то в двоичной системе – лишь две (0 и 1), которые называют битами (двоичными цифрами).

В любой системе кодирования должно выполняться неравенство N < Sn, где N – количество кодируемых объектов; 5 – основание кода (основание системы счисления); п – длина кода (количество разрядов в коде-числе).

Например, для кодирования количества "тринадцать" в десятичной системе счисления достаточно двухразрядного кода 13 < 102, а в двоичной необходим четырехразрядный код 13 < 24 = 16, как показано в табл. 3.1.

Для хранения и обработки информации в виде текстов, формул и чисел необходимо с помощью бит закодировать около 150 различных символов (заглавные и строчные буквы латинского и русского алфавитов, знаки препинания, математические знаки, десять цифр и т.п.), т.е. N = 150. Для этого необходимы восьмиразрядные коды (150 < 28 = = 256). Восьмиразрядный код называют байтом. Емкость памяти ЭВМ оценивают в килобайтах (Кбайт), мегабайтах (Мбайт) и гигабайтах (Гбайт).

В табл. 3.2 приведены примеры двоичного кодирования знаков, латинских букв и десятичных цифр.

Таблица 3.2

Символ	Код	Символ	Код	Символ	Код
А	11000001	0	11110000	7	11110111
а	10000001	1	11110001	8	11111000
В	11000010	2	11110010	9	11111001
b	10000010	3	11110011	Точка	01001011
C	11000011	4	11110100	Плюс	01001110
c	10000011	5	11110101	Минус	01101101
D	11000100	6	11110110

В кодах табл. 3.2, например, величина -6.285 будет закодирована так:

01101101 1111011001001011 11110010 11111000 11110101.

(минус) (шесть) (точка) (два) (восемь) (пять)