Основные задачи, модели и методы технологии когнитивного моделирования

Когнитивные модели. Когнитивная структуризация начинается с определения объектов (характеризуемых как количественно, так и качественно, вербально) изучаемой с определенной целью системы и установление связей между ними. Эти действия осуществляются с помощью экспертов, путем

Рис. 6.16. Схема методологии когнитивного моделирования

сбора и обработки статистической информации, на основании изучения литературных данных, они базируются на теоретических знаниях в соответствующей предметной области.

В результате когнитивной структуризации происходит разработка формального описания знаний, которое можно наглядно изобразить когнитивной моделью (в виде схемы, графа, матрицы, таблицы или текста). Разработка когнитивной модели — наиболее творческий и слабоформализуемый этап в деятельности исследователя (группы экспертов) большой системы. Частично формализация возможна при обработке численных данных в виде статистической информации путем использования средств интеллектуального анализа данных (например, Data mining). Источниками информации для определения "качественных" вершин могут служить теоретические сведения в изучаемой предметной области и согласованные решения группы экспертов. В последнем случае разрабатывается "коллективная когнитивная карта".

Следует обратить внимание на необходимость "правильного" названия вершины — неудачно подобранные названия (концепты) искажают результаты исследования и могут давать ответы не на те вопросы, на которые желательно было бы получить ответы.

Итак, итогом процесса идентификации сложной системы на первом этапе исследования является когнитивная карта G, которая может рассматриваться как "начальная" или "стартовая". Останется ли она неизменной, как окончательная, или пет — решение зависит от эксперта после всех этапов когнитивного моделирования.

В технологии когнитивного моделирования используются различные типы когнитивных моделей.

Наиболее употребимыми являются: когнитивная карта (неформальная когнитивная карта, с ее разработки начинается исследование), а также взвешенный знаковый орграф, простейший функциональный граф, параметрический векторный функциональный граф, модифицированный граф.

Когнитивная карта (в первоначальном понимании — схема причинно-следственных связей в системе) — это структурная схема отношений между объектами ("концептами", "сущностями", элементами, подсистемами) сложной системы; строится для того, чтобы понять и проанализировать се структуру и поведение.

С формальной точки зрения когнитивная карта — это знаковый ориентированный граф (орграф), в котором отражена схема отношений между изучаемыми объектами — вершинами. Отношение между ними (взаимодействие факторов) — это количественное или качественное описание влияния изменения в одной вершине на другие:

где V — множество вершин, вершины ("концепты") V,- е V, ¿=1,2, к являются элементами изучаемой системы; Е — множество дуг, дуги е Е, I,) =1,2, п отражают взаимосвязь между вершинами У;и Му Влияние г",-на ь) в изучаемой ситуации может быть положительным (знак "+"), когда увеличение (уменьшение) одного фактора приводит к увеличению (уменьшению) другого, отрицательным (знак "-"), когда увеличение (уменьшение) одного фактора приводит к уменьшению (увеличению) другого, или отсутствовать (0). В последнем случае соответствующую дугу можно было бы исключить при анализе данной ситуации, но она может иметь значение в другой ситуации. Поэтому, если предполагается такая возможность, дугу нужно оставить.

Когнитивная карта помимо графического изображения может быть представлена матрицей отношений Ас:

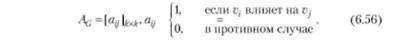
Матрица Л(; — это квадратная матрица, строки и столбцы которой помечены вершинами графа С а на пересечении г-строки и ./-столбца стоят единицы (или 0), если существует (не существует) отношение между элементами V; и Уу В когнитивной карте отношение может иметь знак "+1" или "-1".

Когнитивная карта отображает лишь факт наличия влияния вершин (факторов) друг на друга. В ней не отражаются ни детальный характер этих влияний, ни динамика изменений влияний в зависимости от изменения ситуации, ни временные изменения самих факторов. Учет всех этих обстоятельств требует перехода на следующий уровень структуризации информации, отображенной в когнитивной карте, т.е. требуется переход к другим тинам когнитивной модели.

На уровне когнитивной модели каждая связь между факторами когнитивной карты раскрывается до соответствующего уравнения, которое может содержать как количественные (измеряемые) переменные, так и качественные (неизмеряемые) переменные. Количественные переменные входят в модель в виде их численных значений. Каждой качественной переменной может быть поставлена в соответствие совокупность лингвистических переменных, отображающих различные системы этой качественной переменной на шкале [0; 1 ].

По мере накопления знаний о процессах в системе становится возможным более детально раскрывать характер связей между вершинами — факторами (например, с помощью процедур data mining, если есть таблицы статистических данных).

Когнитивная модель типа векторный функциональный граф — это кортеж

где С = < V, Е> — ориентированный граф; X — множество параметров вершин V; X = [ХЩ, 1=1,2,.... к, Х(и> = {^}, ё = 1, 2, щ, т.е. каждой вершине ставится в соответствие вектор независимых друг от друга параметров Х(у' (или один параметр х№>8=Х, если g= 1); X : V -> Я, Я — множество вещественных чисел; Р= Е(Х, Е) = Дд:;, Хр е$) — функционал преобразования дуг, ставящий в соответствие каждой дуге либо знак ("+", "-"), либо весовой коэффициент <о^, либо функцию хр ец) =и

В зависимости от Е(Х, Е) вводится расширенное понятие орграфа.

1. Когнитивная карта (знаковый орграф) как частный случай Ф-графа, в котором

где со^- — весовой коэффициент; со^ е. IV, V/ — множество весовых коэффициентов дуг — множество вещественных чисел. Оценка со- может определяться одним числом или быть интервальной.

3. Простейший функциональный граф — это Ф-граф, в котором Е= ДХ, Е) =/(я$, Хр е$ =/}/.

где /у — это функциональная зависимость параметров вершин, которая ставится в соответствие каждой дуге. Зависимость /у может быть не только функциональной, но и стохастической. Определение параметров характеристики /у включает: определение шкалы, показателей, метода, точности, единицы измерения.

Определение Ф-графов может быть обобщено нижеследующим образом.

4. Параметрический векторный функциональный граф Фп — это кортеж

где б = < V, Е > — ориентированный граф; X : V -" 0, X -множество параметров вершин, X = {->№> | Х<г'> е X, i = 1,

2, к }, Х('';> = {.г*,0}, g 1,2.....к х^ — £-параметр вершины

У;, если £= 1, то л-*,'* = х,-; 0 — пространство параметров вершин; /г= Е(Х, Е) — функционал преобразования дуг, Е.Ех. х X х 0 -> К

5. Модифицированные МФ-графы. Для отражения динамики происходящих в системе под воздействием всевозможных возмущений изменений в модель вводится время. Такие графы предложены в работе.

Иерархические когнитивные карты. Сложным системам присуща закономерность иерархичности. Для отражения такой структуры могут быть использованы иерархические когнитивные карты — сравнительно новый тип когнитивных моделей. Иерархические когнитивные карты представляют собой раскрытие обобщенных объектов (вершин) верхнего уровня когнитивной карты в составляющие их объекты, в том числе объекты нижних уровней. Количество иерархических уровней может определяться как количеством "раскрываемых" в когнитивные карты вершин, так и существующей системой управления объектом (например, уровни государства, региона, муниципалитета). Рисунок 6.17 иллюстрирует эту идею.

Рис. 6.17. Модель сложной системы в виде иерархической когнитивной карты

Модель иерархической когнитивной карты имеет вид

где и — когнитивные карты к- и (&-1)-уровней соответственно, Ек = {етКр)} — отношения между вершинами к- и р- уровней.

Когнитивная карта ^-уровня представляет собой ориентированный граф

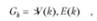
где У(£) = {г;Д£)|г;Д&) У(Щ,1 1,2р... и} — множество вершин

^-уровня, Е(к) = |е0'(£)|е$'(£) £(<£); I,./' 1,я} — отношения, отражающие взаимосвязь между вершинами внутри уровня (^-уровня).

Структурное объединение иерархической когнитивной модели в виде функционального графа будет иметь вид

где Ю ч бд.,, вк, Бц 2 — когнитивная иерархическая кар-

та; Хк = []Х(к) — множество параметров вершин иерархической когнитивной карты; ^ = {?(Х,£^);и^(*)} — функционал 1=1 преобразования дуг в иерархической когнитивной модели.

Можно представить несколько взаимодействующих объектов, функционирующих в определенной окружающей среде. При этом необходимо строить когнитивные модели более сложного типа — модели взаимодействия иерархий, отношения между которыми задаются правилами теории игр. Так, иерархии могут находиться в отношениях сотрудничества (кооперации, коалиции) или противоборства (конкуренции). Возможно обобщение на случай взаимодействия N сторон — общая модель представляет собою систему иерархических когнитивных моделей, в которой заданы правила взаимодействия и правила изменения структуры когнитивных моделей.

Динамические когнитивные карты. По результатам исследований в области взаимодействия сложных систем использовались когнитивные модели в виде динамических когнитивных карт, в которых параметры модели зависели от времени и учитывались временные изменения среды.

Задачи анализа путей и циклов когнитивной модели

Решение задачи анализа путей и циклов когнитивной модели производится традиционными методами теории графов. Выделение путей различной заданной длины позволяет проследить и интерпретировать цепочки причинно-следственных связей, выявляя их особенности и противоречия. Выделение циклов (положительных и отрицательных обратных связей) позволяет судить о структурной устойчивости (или нет) системы.

Если проанализировать карту "Проблемы потребления электроэнергии" (см. рис. 6.14), то в ней наблюдается пять циклов: К-> Ух-> V* У^ У"> Ух-> К* Ц>"> ^4"> ^3">

-> Vq, V7-> V5 -" VA -> V3 -" V6 -" V7, среди которых V5 -> -> Kj -> ^2~^ ^5 — один отрицательный.

Сценарии поведения объекта, импульсное моделирование (сценарное моделирование)

Моделирование поведения системы основано на сценарном подходе.

Сценарию с фундаментальной точки зрения соответствует Вперед онтология: начальное состояние, последовательность событий, конечное состояние. Другими словами, метафорически сценарий структурируется во временном измерении схемой "источник — путь — цель", где источник — это начальное состояние, конечное состояние — это место назначения, события — это нахождение в пути, а путь растянут во времени.

Сценарий — это целое, а каждый из элементов — часть.

Онтология сценария обычно включает также людей, вещи, свойства, отношения и пропозиции. Кроме того, элементы онтологии часто связываются отношениями определенных типов: причинными отношениями, отношениями тождества и т.д. Эти отношения структурно представляются схемами связи (link schémas), каждая из которых категорируется в соответствии с типом связи, которую она представляет. Сценариям присущи также целевые структуры, которые специфицируют цели участников сценария.

Определение понятия "сценарий" связано с определением понятий "признаки системы", "состояние системы", "поведение системы", "ожидаемое событие", "ситуация".

Признаки характеризуют свойства системы, подсистемы и элементы. Признаки могут быть качественными и количественными. Признак может быть мерой эффективности. Измерить признак часто является серьезной проблемой.

Состояние системы характеризуется значениями признаков в данный момент времени. Состояния системы меняются в процессе ее функционирования.

Переходы системы (или ее частей) из состояния в состояние вызывают потоки, определяемые как скорость изменения значений признаков системы.

Поведение системы — это изменение состояний системы во времени.

Ожидаемое событие поведения объекта, согласно разработанной модели объекта, — это тройка: момент времени t, выбранный в соответствии с некоторыми правилами выбора А (правило выбора А указывает моменты времени для фиксации траектории повеления объекта), дг(г) и г/(г) — ожидаемая реализация параметров описания окружающей среды и фазовой траектории системы.

Ситуация 5(0 в момент времени г — это хронологизируемый во времени набор событий, произошедших до момента Ь.

Сценарий — это совокупность тенденций, характеризующих: ситуацию в настоящий момент, желаемые цели развития, комплекс мероприятий, воздействующих па развитие ситуации, и системы наблюдения параметров (факторов), иллюстрирующих поведение процессов.

Определяют глубину сценария, горизонт сценария, временной шаг сценария. Представляют сценарий в формализованном виде.

Сценарий может моделироваться по трем основным направлениям:

• прогноз развития ситуации без всякого воздействия на процессы: ситуация развивается сама по себе (эволюционное развитие);

• прогноз развития ситуации с выбранным комплексом мероприятий-управлений (прямая задача);

• синтез комплекса мероприятий для достижения необходимого изменения состояния ситуации (обратная задача).

Моделирование распространения возмущений на когнитивных картах, импульсные процессы. Объект моделирования можно рассматривать как совокупность взаимодействующих между собой динамических процессов, протекающих в реальном времени. В модели процессов также должно присутствовать время, но при моделировании разными типами графов это время может не иметь смысла времени, а отражать только последовательность изменений состояний. Это имеет место для знаковых орграфов и знаковых параметрических графов. Для описания взаимодействия со средой используют понятия "вход", "выход", "состояние", "поведение" системы.

При анализе ситуаций, опирающемся на модели когнитивных карт, решаются два типа задач: статические и динамические. Статический анализ — это анализ текущей ситуации, включающий исследование влияний одних факторов на другие, исследование устойчивости ситуации в целом и поиск структурных изменений для получения устойчивых структур.

Динамический анализ — это генерация и анализ возможных сценариев развития ситуации во времени. Математическим аппаратом анализа является теория знаковых графов и нечетких графов.

Под влиянием различных возмущений значения переменных в вершинах графа могут изменяться; сигнал, поступивший в одну из вершин, распространяется по цепочке на остальные, усиливаясь или затухая.

Импульсное моделирование — это моделирование распространения возмущений на когнитивных картах, вызываемого внесением возмущений-импульсов в вершину (совокупность вершин) когнитивной карты. Объект моделирования можно рассматривать как совокупность взаимодействующих между собой динамических процессов, протекающих в реальном времени.

Сценарный анализ позволяет судить о поведении системы, научно предвидеть пути ее возможного развития. Анализ проводится по результатам импульсного моделирования. Для генерирования возможных сценариев развития системы в вершины когнитивной карты вносятся гипотетические возмущающие или управляющие воздействия. При внесении возмущений <2,(и) исследуется вопрос "что будет в момент (и + 1), если...?". Набор реализаций импульсных процессов — это "сценарий развития", он указывает на возможные тенденции развития ситуаций.

Импульсный процесс может отображать как эволюционное развитие системы, так и ее развитие под воздействием возмущений и управляющих воздействий 0,^), вносимых в вершину 1>1 в момент г„.

Сценарием развития ситуаций принято называть всю совокупность импульсных процессов во всех вершинах когнитивной карты. Таким образом, совокупность импульсных процессов при внесении возмущений <2 представляет собой модельную реализацию альтернативных действий (Л Для реальных систем 0_ интерпретируется как различные управленческие (например, программы развития системы) или возмущающие воздействия (например, изменения во внешней среде, действия конкурента и др.).

Генерируемые при различных возмущающих воздействиях сценарии развития фактически являются "научным предвидением" возможных путей развития системы. Сценарий характеризует тенденцию развития процессов в системе, точнее, различные возможные тенденции развития (следствия) при гипотетических изменениях возмущающих и управляющих факторов и их сочетаний (причины) в моделируемом будущем. Таким образом, импульсное моделирование развития ситуаций позволяет разрабатывать возможные сценарии развития системы — от пессимистичных до оптимистичных. На основании сценариев проектируется стратегия управления системой, которая далее реализуется лицами, принимающими решения, в соответствии с диктующими условиями внешней и внутренней среды.

Рассмотрим правило (РЯ) изменения параметров в вершинах в момент Пусть параметр х! зависит от времени, т.е. Х}(1)у 1= 1, 2, 3,.... Тогда можно определить процесс распространения возмущения по графу, т.е. переход системы из состояния £ - 1 в и I + 1,....

В общем случае, если имеется несколько вершин смежных с V,-, процесс распространения возмущения по графу определяется правилом (при известных начальных значениях Х(0) во всех вершинах и начальном векторе возмущения Р(0)):

где дг,(0 и х£1 + 1) — значения параметра в вершине V; в моменты Ьу I + 1, р^£) — изменение в вершине У^ в момент времени Г,

Так как в Ф-графе импульс в импульсном процессе представляется упорядоченной последовательностью без привязки ко времени, то можно использовать запись формул "в и-й момент времени" (в модели процессов при моделировании разными типами графов время может не иметь смысла времени, а отражать только последовательность изменений состояний. Это имеет место для знаковых орграфов и знаковых взвешенных орграфов). Функцию ру(/;) влияния изменения в смежной с У-} вершине V) можно заменить импульсом р(п) = х(п + 1) - х(п), где х(п)у х(п + 1) — величины показателя в вершине V при шагах имитации в момент £ = п и следующим за ним £ = п + 1. Тогда формула (6.64) преобразуется к виду

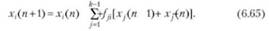
Правило (Рй) изменения параметров в вершинах в момент £и+1, если в момент времени іп в вершины поступили импульсы:

Модель импульсного процесса — это кортеж (Ф. £>, РЩ, где ф — Ф-граф, (2= 0,(1,,) — последовательность возмущающих воздействий, РЯ — правило изменения параметров. При этом последовательность Х(г0),<2(гн)^ является модельным представлением динамической системы (г0,50,В0).

Для разработки соответствующих вычислительных алгоритмов удобно математическую модель импульсных процессов на знаковых графах представить в матричном виде.

і = 0, 1, 2, вносимых в вершины У; в момент времени £; вектор параметров вершин в момент времени г и изменения параметров вершин задаются уравнениями:

Для R, из последнего уравнения получим выражение

где / — единичная матрица.

Автономными называют частный случай импульсных процессов на когнитивных картах, когда внешние импульсы вносятся только один раз в начале моделирования.

Простейшим вариантом распространения возмущения является случай, когда Р(0) имеет лишь один ненулевой вход, т.е. возмущение поступает только в одну вершину V-r Такие процессы принято называть простыми процессами.

Ситуация в импульсном моделировании характеризуется набором всех Q и значений X в каждом п такте моделирования.

Приведем пример импульсного моделирования по когнитивной карте проблем потребления электроэнергии (рис. 0.19). Для нее матрица отношений имеет вид

Промоделируем процесс распространения возмущении по когнитивной карте проблем потребления электроэнергии: "Что будет, если потребление электроэнергии возрастет?" (рис. 6.18). Как видно по графикам импульсных процессов, тенденции развития ситуаций не противоречат интуитивным предположениям о том, что рост потребления электроэнергии из-за нарастания энергетической мощности может привести к падению ее стоимости, ухудшению состояния окружающей среды, росту числа предприятий, росту числа рабочих мест. На графиках по оси ОХ отложены такты моделирования п, но оси 0У цифры характеризуют скорость нарастания сигналов в вершинах когнитивной карты (научное предвидение возможных тенденций развития).

Рис. 6.18. Сценарий № 1. Рост потребления электроэнергии, <7/(= +1, вектор возмущений (2= (0,0,0 + 1,0,0,0)

Обратные задачи, задачи управляемости и наблюдаемости

Решение обратной задачи — это поиск таких значений управляющих воздействий (2, которые могут обеспечить желаемый сценарий развития системы. Для решения могут быть использованы методы математического программирования (линейного, нелинейного).

Решения задач наблюдаемости и управляемости системы взаимосвязаны. Задача наблюдаемости — задача определения достаточности измерений выходных переменных для определения неизвестных начальных значений входов. Задача управляемости — это задача о возможности изменения входов системы в зависимости от наблюдаемых выходов (кибернетический или управленческий подход).

Анализ устойчивости системы, представленной графом

Устойчивость — понятие многоаспектное. В исследованиях социально-экономических систем термин "устойчивость" обозначает очень многое, не всегда четко определенное (устойчивость финансовой системы, устойчивость организации). В теории управления техническими системами понятие "устойчивость" определяется четко, разработаны критерии устойчивости системы ("устойчивость по Ляпунову", по Пуанкаре и др.). Рассматривают два аспекта понятия "устойчивость": устойчивость системы под воздействием внешних возмущений при фиксированной структуре системы, т.е. когда изменяется только внешняя среда, и устойчивость поведения системы при изменениях структуры системы — структурная устойчивость (малые изменения в структуре системы вызывают малые изменения в ее динамике).

При исследовании устойчивости взвешенного ориентированного графа — когнитивной карты — исследуется устойчивость по значению и устойчивость по возмущению системы по мере ее эволюции.

Представим понятия алгебраического критерия устойчивости по возмущению и начальному значению и рассмотрим связь устойчивости графа с его топологической структурой, опираясь на работы В. В. Кульбы, С. С. Ковалевского, Д. Л. Кононова, А. Б. Шелкова и др., а также на работах Дж. Каста.

Основополагающим представлением при разработке критериев устойчивости графов является представление о характеристических значениях матрицы отношений Л(; графа — когнитивной модели.

Характеристические значения графа определяются как собственные значения матрицы Ас. Согласно теореме Рауса — Гурвица для линейных систем, если среди собственных значений матрицы (корней) нет чисел по модулю больших единицы, то система устойчива по возмущению. Устойчивость по возмущению не означает наличия устойчивости по значению, хотя обратное и справедливо. Но для применения этого критерия имеются существенные ограничения, поэтому использовать его будем в простых случаях.

Для приведенного выше примера проблем потребления электроэнергии (см. рис. 6.18) число корней матрицы Ас равно 7, среди которых имеется корень по модулю больше 1: М= 1,43. Следовательно, эта система неустойчива ни по возмущению, ни по начальному значению. Собственно, факт неустойчивости иллюстрируется и графиками импульсных процессов (см. рис. 6.18) — графики расходятся.

Структурная и связная устойчивость системы

Положение равновесных состояний зависит от динамических свойств изучаемой системы и может изменяться. Поэтому возникает еще один вопрос: поведет ли небольшое изменение системы к смещению состояния равновесия? То есть в отличие от классической теории устойчивости, не рассматривавшей изменения в системе, а только возмущения в окружающей среде, необходимо изучать проблемы устойчивости при структурных изменениях самой системы. Это практически очень важный вопрос, так как эти изменения, даже малые, могут привести к резким качественным изменениям в дальнейшем поведении системы. Одним из инструментов исследования таких явлений является теория катастроф, или теория бифуркаций.

Существует "комбинированное" понятие устойчивости, сочетающее классические идеи Ляпунова с комбинаторно-топологическим подходом, — понятие связной устойчивости, которое первоначально возникло в связи с изучением вопросов равновесия в экономике. При изучении связной устойчивости задача формулируется так: останется ли состояние равновесия данной системы устойчивым в смысле Ляпунова вне зависимости от двойных связей между состояниями системы?

Определим матрицу отношений Ас. Состояние равновесия X = О считается связноустойчивым, если оно устойчиво по Ляпунову для всех возможных матриц взаимосвязи

Изучение связной устойчивости имеет практический интерес, особенно при исследовании организационных систем, таких как экономическая система. Это обусловливается тем, что при описании процессов в этих системах наличие или отсутствие данной связи не всегда может быть очевидным вследствие нарушений работы самой системы, наличия возмущений, известной субъективности математической модели системы.

Адаптивность системы является еще одним аспектом устойчивости. Адаптируемость можно представить себе как определенную меру способности системы к поглощению внешних возмущений без резко выраженных последствий для ее поведения в переходном или установившемся состоянии.

Понятие адаптируемости близко к понятию структурной устойчивости, но несколько шире него.

Рассмотрим основные положения, связанные с исследованием структурной устойчивости систем. Классическое представление об устойчивости является весьма плодотворным в технических и физических системах. Для социотехнических, социально-экономических систем такое представление может быть использовано, но это требует серьезных обоснований для конкретных систем. Тем более что обычный режим функционирования этих систем далек от равновесного, кроме того, внешние возмущения постоянно изменяют само состояние равновесия. Центральным элементом современных взглядов па устойчивость является понятие структурной устойчивости, которое рассмотрим далее.

Основной задачей исследования структурной устойчивости является выявление качественных изменений в траектории движения системы при изменениях структуры самой системы. Возникает необходимость рассматривать группу систем, "близких" к некоторой стандартной, т.е. мы имеем дело с семейством траекторий, которое необходимо исследовать. В такой ситуации говорят о структурной устойчивости.

Систему называют структурно устойчивой, если топологический характер траекторий всех близких к ней систем такой же, как у стандартной.

Таким образом, свойство структурной устойчивости состоит в том, что рассматриваемая система ведет себя почти так же, как и близкие к пей; в противоположном случае — система структурно неустойчива. Уровень структурной устойчивости характеризует обобщенные сведения о степени устойчивости системы или отдельных ее элементов к внешним и внутренним возмущениям заданной природы.

Для всех сформулированных выше задач возникает ряд математических трудностей, связанных с тем, как определить, что такое "малые возмущения", "траектории, близкие к началу координат", "близкие системы", "траектории, типологически подобные одна другой". Для некоторых конкретных классов систем эти трудности преодолены.

Можно выделить две группы методов математического анализа структурной устойчивости модели, записанных на языке знаковых орграфов. Первый основан на ряде теорем, связывающих спектр орграфа с его устойчивостью в простых импульсных процессах, второй — на преобразовании исходного знакового орграфа в матричную модель с подробным анализом последней. Структурная устойчивость системы может быть установлена путем анализа циклов когнитивной карты.

При анализе когнитивной карты путем выделения в ней циклов используют понятия четного и нечетного циклов. Мы уже упоминали выше о циклах положительной и отрицательной обратной связи. Между типом цикла и устойчивостью системы существует взаимосвязь.

Четный цикл является простейшей моделью структурной неустойчивости, так как любое начальное изменение параметра в любой его вершине приводит к неограниченному росту модуля параметров вершин цикла. Любое изменение параметра любой вершины нечетного цикла приводит лишь к осцилляции параметров вершин. Знаковый орграф, не содержащий циклов или содержащий лишь один цикл, импульсно устойчив для всех простых импульсных процессов.

До сих нор речь шла о формальном анализе устойчивости когнитивных карт сложных систем. Нужно иметь в виду еще один из серьезных аспектов исследования устойчивости когнитивных карт, используемых в других направлениях когнитивных исследований. В этом смысле анализ устойчивости когнитивных карт заключается в определении сбалансированных, согласованных, устойчивых когнитивных структур и, в концептуальном плане, базируется па основных положениях теорий социальной психологии: когнитивного диссонанса Л. Фестингера, структурного баланса Ф. Хайдера, коммуникационных актов Т. Ньюкома.

Задача сложности и связности системы

Понятие "связность" системы возникает вместе с понятием "структура" системы. С исчезновением структурной связности исчезает система. Математическое описание задачи анализа связности удачнее всего получается на языке теории графов и алгебраической топологии. Первый способ основан на анализе связности графовой модели методами теории графов. Второй подход основан на исследовании топологических свойств графовой модели по матрице отношений когнитивной карты, так называемый ^-анализ связности симплициальных комплексов. Основы топологического исследования сложных систем на основе изучения их структурных свойств были начаты в 1960—1970-е гг. В настоящее время показана эффективность использования симплициальных комплексов для моделирования свойств связности различных сетей взаимодействующих элементов (подсистем, сущностей...), таких как коммуникации, трафики, биологические сети, сети распределенных алгоритмов. Доказано, что симплициальные комплексы весьма полезны при исследованиях динамических процессов в сетях.

Математические основы полиэдрального анализа были заложены К. Дроукером, а дальнейшее развитие анализ получил в работах британского физика Р. Эткина. Им был разработан первый инструмент симплициального анализа, названный ^-анализом (полиэдральный анализ, или анализ полиэдральной динамики). Несмотря на то что приложение ^-анализа к исследованию социальных, биологических, экономических и других сложных систем показало свою эффективность, публикаций в этом направлении не так много (из ранних — это работы Р. Эткипа, Дж. Касти, С. Сейдмана, Дж. Джонсона, К.Эрла, П. Гоулда, X. Кауклклиса, С. Макгилла, А. Куллена, X. Гриффита, Г. Варселло, X. Крамера, Р. Аксельрода, Р. Лаубенбахера). В нашей стране последние годы также начал наблюдаться интерес к применению методов топологии в изучении структур сложных систем (например, В. Б. Мнухин, О. Ю. Катаев и др.)" но эти и другие математические работы носят теоретический характер, и применительно к изучению социально-экономических систем такие исследования сейчас крайне малочисленны. Методика анализа {/-связности позволяет судить о связности системы более глубоко, нежели традиционные исследования связности графа, поскольку при этом устанавливается наличие взаимовлияния симплициальных блоков системы через цепочку связей между ними. На основании таких возможностей предлагаются формализованные правила обоснования выбора целевых и управляющих вершин, определение устойчивости систем, характеризуемых теми или иными симплициальными комплексами, условия структурной устойчивости систем. Определение числа симплексов и их структуры, анализ ^-связности системы позволяют выдвигать обоснования для решения задач декомпозиции и композиции изучаемой социально-экономической системы, выявлять симплексы, более всего влияющие на процессы в системе и образующие вершины которых рациональнее выбирать в качестве управляющих. ф- анализ позволяет раскрыть многомерную геометрию сложных систем, проследить влияние различных локальных изменений на структуру системы в целом, остановить внимание именно па структурных особенностях системы, что не выявляется при других подходах. Использование этого метода для анализа структурно сложных систем позволяет по-другому подойти к самому определению понятия "сложность", более глубоко вскрыть роль отдельных элементов п их влияние на остальные элементы системы.

Сошлемся на параграф 7.4, в котором изложены основы анализа ^-связности системы. В этом анализе система рассматривается в виде отношения между элементами конечных множеств — множества вершин Ун заданного семейства непустых подмножеств этих вершин — симплексов а. Множества вершин и соответствующих им симплексов образуют симплициальные комплексы К. Для их построения могут быть использованы специальные приемы построения (экспертные) матрицы инциденций Л:

но может быть использована готовая структура системы, заданная в виде графа С = <У, £>, которая служит основанием для геометрического и алгебраического ее представления как симплициального комплекса. Симплициальный комплекс состоит из множества вершин {У} и множества непустых конечных подмножеств множества {V,-}, называемых симплексами (симплициальный комплекс получается путем разбиения некоторого пространства X (или У) на пересекающиеся подмножества; пространство, допускающее такое разбиение, называется полиэдром, а процесс его разбиения — триангуляцией).

Симплекс обозначается как 8^)^, где і — номер вершины, а ц — геометрическая размерность симплекса. Число д определяется числом дуг, соединяющих вершины У} в симплексе через переменную хг Число ц (число дуг, инцидентных у-) на единицу меньше числа единиц ("") в соответствующей /-строке матрицы Л. Если в строке матрицы Л отсутствует 1, то размерность "пустого" симплекса обозначим: # = О -- 1 = -1. Размерность симплекса — это число ребер в каждой вершине полного графа — симплекса.

Цепочки ^-связности образуются через соединения одноименных вершин. Цепь связи отражает возможность того, что два симплекса, непосредственно не имея общей грани, могут быть связаны при помощи последовательности промежуточных симплексов.

Не давая строгих определений анализа ^-связности (см. параграф 7.4), проиллюстрируем построение симплициального комплекса примером проблем потребления электроэнергии (для ПС КМ разработаны специальные алгоритмы построения симплициальных комплексов большой размерности). По матрице Ас можно определить ее симплициальные комплексы — по строкам КХ(У, X) и по столбцам Ку(Х, X*), где X — строки, У — столбцы, X — матрица отношений между элементами (Ас), X* — транспонированная матрица.

Построим комплекс КХ(У, X) — по строкам.

Первая строка, \: §(1)б/=і і=и. симплекс состоит из одной вершины УА.

^2- &2=-ио> симплекс состоит из одной вершины У$ . У: 8^/=2-=у симплекс состоит из взаимосвязанных через У двух вершин — Ух и Уе.

У: 8*4^_з_1=2, симплекс состоит из трех вершин — У^ У и У$.

У$: 8<5)^=]_1=0т симплекс состоит из одной вершины УА. У§. 8^6^д-2-1=1" симплекс состоит из двух вершин — У и У-г

У7: 8(7^=3_1=0, симплекс состоит из одной вершины УГг Таким образом, симплициальный комплекс имеет вид: ВД Я.) = {8(1)9=0; 5(2)^,; 8(3>9=2; 8(4)д=3; б^; 80)^}.

Поскольку в этом комплексе нет симплексов размерности более 2, его можно изобразить геометрически на плоскости (рис. 6.19).

Рис. 6.19. Геометрическое представление симплициального комплекса Кх( У, X)

Как видим, комплекс несвязный, в нем имеется три отдельных компоненты, что может говорить о слабой управляемости данной структуры.

Понятия связности и сложности системы взаимообусловлены. Рассматривают: структурную сложность, динамическую сложность, вычислительную сложность, эволюционную сложность; внутреннюю и внешнюю сложность. Для того чтобы система реализовала заданный вид поведения вне зависимости от внешних помех, подавить многообразие в ее поведении можно, только увеличив множества управлений (принцип необходимого многообразия Эшби). Такая способность системы характеризует "сложность управления". Система не может быть "универсально сложной". Она может быть сложной с одних позиций и несложной с других. "Сложность" систем часто приводит к тому, что проще сначала изучить элементы, компоненты системы, а затем, на основании полученных знаний, попытаться понять систему в целом. Поэтому задача анализа сложности системы связана с проблемами декомпозиции и композиции системы.

Методы построения когнитивных моделей сложных систем

Методы построения когнитивных моделей должны: отвечать требованиям удобства и конструктивности; быть тесно связаны с методами оценок результатов анализа так, чтобы в процессе принятия решений когнитивная модель могла служить советчиком и критиком ЛПР; точно отражать представления ЛПР о концептах и отношениях между ними; не должны требовать от составителя когнитивной модели предварительной спецификации концептов.

В настоящее время предлагается большое количество способов построения когнитивных моделей сложных систем. Но все это ближе к искусству, чем к строгим правилам, хотя разработано большое количество инструментальных средств, помогающих исследователю разработать ту или иную когнитивную карту. Обобщить эти способы можно следующим образом:

• разработка когнитивных моделей (когнитивных карт) с помощью специалистов в предметной области. Применяются различные экспертные методы и технологии работы с экспертами (в том числе работа в ситуационных центрах; для этого разработано достаточно вариантов специального программного обеспечения, например АрхиДока, разработчик некоммерческое партнерство но научным исследованиям и социальному развитию Аналитическое агентство "Новые стратегии", руководитель А. Н. Райков);

• разработка когнитивных моделей исследователем (инженером-когнитологом) совместно со специалистом в предметной области;

• разработка когнитивных моделей (или их блоков) но результатам статистического анализа данных с помощью программ Data-mining, а также с помощью специального программного обеспечения (например, компьютерный ЖОК-метод, разработчики В. Н. Жихарев, А. И. Орлов, В. Г. Кольцов);

• разработка когнитивных моделей на основании анализа текстов, содержащих информацию о предметной области;

• разработка когнитивных моделей на основании анализа существующих теорий в предметной области, использование готовых когнитивных схем.

При разработке когнитивных карт с помощью экспертов можно рекомендовать следующие методы.

1-й метод. Когнитивную карту строит сам ЛПР на основе своих знаний и представлений без привлечения экспертов и справочных материалов.

Достоинство метода: быстрота построения когнитивной карты. Недостаток: адекватность когнитивной карты сильно зависит от квалификации ЛПР, его знания и умения ощущать характер отношений между концептами.

Построение когнитивной карты помогает ЛПР яснее представить себе проблему, лучше понять роль отдельных компонентов и характер отношений между ними.

2-й метод. Построение когнитивных карт экспертами на основе изучения документов.

Достоинство: метод удобен и позволяет использовать данные, применяемые самим ЛПР. Недостаток: изучение документов экспертами — длительный и трудоемкий процесс.

3-й метод. Построение когнитивной карты на основе опроса группы экспертов, имеющих возможность оценивать причинно-следственные связи.

Достоинство: возможность агрегировать индивидуальные мнения и базирование на большем диапазоне оценок, чем можно извлечь из изучаемых документов. Недостаток: трудоемкость.

4-й метод. Построение когнитивных карт, основанных на открытых выборочных опросах. Достоинства: метод может быть использован для построения сравнительных когнитивных карт, кроме того, исследователю представляется возможность вести активный диалог с источниками информации. Недостаток: трудоемкость.

Подробный пример разработки когнитивных карт с помощью экспертов приведен в в работах сотрудников ИПУ РАН, например в книге Э. А. Трахтенгерца, а также в работах.

Если проводится когнитивное моделирование реальной социально-экономической или другой сложной системы, можно рекомендовать применение сочетания этих методов и приемов.

Адекватность модели

Эффективность применения когнитивной модели на практике зависит от ее соответствия реальной обстановке. Неадекватность модели при использовании ее для разработки стратегий развития системы и принятия управленческих решений может иметь гораздо более масштабные отрицательные последствия, нежели неудачная когнитивная модель, построенная индивидуумом в процессе повышения своего 1£) (в экспериментах когнитивных психологов показано, что техника когнитивных карт является одной из наиболее эффективных техник мышления, использующая оба полушария мозга, повышающая уровень интеллекта, развивающая память и т.д.). Проверка адекватности когнитивной модели — это одна из неоднозначно решаемых проблем.

В общем виде эту проверку можно осуществить следующим образом.

Пусть между базисными факторами, являющимися вершинами графовой модели, существуют отношения, которые можно трактовать как всевозможные аксиомы предметной области. Как правило, эти отношения формируются в виде продукций типа:

где Х;, г = 1,2.....к — некоторая характеристика базисного фактора V-, (например, предельная величина фактора, знак приращения фактора и т.п.). Совокупность таких продукций образует базисные знания о данной предметной области.

Графовая модель считается адекватной реальной ситуации, если в модельных процессах не нарушается ни одна из продукций базисных знаний.

Полнота проверки модели на адекватность зависит от полноты базисных знаний, которая определяется по отношению числа состояний ситуации, отраженных в базисных знаниях, к полному числу состояний ситуации.

Если базисные знания об исследуемой ситуации отсутствуют, поведение процессов в прошлом может никак не влиять на их будущее поведение. Поэтому никакое приемлемое прогнозирование этих процессов невозможно.

Таким образом, с самых общих позиций проверка адекватности модели — это сравнение информации о реально моделируемой системе, которая получена эмпирическим путем в некоторой области параметров системы, с той информацией, которую в той же области параметров системы дает модель. Если расхождения невелики с точки зрения целей моделирования, то модель считается адекватной.

Качество и результативность когнитивного анализа связаны как с субъективностью ЛПР, так и с тем фактом, что само исследование влияет на результаты. Существует взаимосвязь между мышлением участников и ситуацией, в которой они участвуют. Эта взаимосвязь проявляется двояко, в виде двух зависимостей: когнитивной (пассивной), выражающей усилие участников, затрачиваемое на понимание ситуации, и управляющей (активной), связанной с действием их умозаключений на ситуацию в реальном мире. В когнитивной функции восприятия участников зависят от ситуации, а в управляющей функции они влияют на ситуацию.

Таким образом, наличие в системе мыслящих участников, каждый из которых по-своему представляет ситуацию и принимает те или иные решения, исходя из своего "виртуального" представления, приводит к тому, что, по словам Дж. Сороса, "...последовательность событий не ведет напрямую от одного набора факторов к другому; вместо этого она перекрестным образом соединяет факторы с их восприятием, а восприятия с факторами".

Это приводит к тому, что процессы в ситуации ведут не к равновесию, а к никогда не заканчивающемуся процессу изменений. Отсюда следует, что в результате взаимодействия как ситуация, так и взгляды участников являются зависимыми переменными и первичное изменение ускоряет наступление дальнейших изменений как в самой ситуации, так и во взглядах участников. Схема когнитивного моделирования на рис. 6.17 предусматривает этот факт. Убежденность исследователя в адекватности модели возникает или нет как в результате решения каждой системной задачи в отдельности, так и в сопоставлении всех результатов в комплексе.

Так, например, если тенденции развития ситуаций по какому-либо моделируемому сценарию развития, соответствующему конкретному состоянию социально-экономической системы, не противоречат наблюдаемым тенденциям процессов в реальной системе (временные ряды статистических данных), то такая графовая модель может считаться адекватной. Или если разработанная структура — когнитивная карта — неустойчива, а в реальности наблюдается устойчивость исследуемой системы, то возникает естественное сомнение в разработанной модели. Численной меры адекватности всех результатов в совокупности не разработано (пока остается открытым и вопрос, возможно ли это сделать в принципе), приходится возвращаться к общему определению: "графовая модель считается адекватной реальной ситуации, если в модельных процессах не нарушается ни одна из продукций базисных знаний".

Проблемы адекватности когнитивных моделей не перестают волновать исследователей. И в настоящее время коллективом Сектора 51 ИПУ РАН ведутся серьезные работы в области проверки когнитивных карт. Используются понятия "неформальных" и "формальных" когнитивных карт. Так, рисунки когнитивных карт данного параграфа относятся к неформальным картам. Параметрические функциональные графы можно отнести к формальным.

Пример применения технологии когнитивного моделирования приведен в приложении 6.