Оптимизация сетевых моделей

Для оптимизации сетевой модели, выражающейся в перераспределении ресурсов с ненапряженных работ на критические для ускорения их выполнения, необходимо как можно более точно оценить степень трудности своевременного выполнения всех работ, а также "цепочек" пути. Более точным инструментом решения этой задачи по сравнению с полным резервом является коэффициент напряженности, который может быть вычислен одним их двух способов в соответствии с приведенной ниже формулой:

(3.56)

где 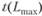– продолжительность максимального пути, проходящего через работу (i,j);

– общая продолжительность отрезков пути, проходящего через работу (i,j), совпадающих с критическим путем.

Коэффициент напряженности изменяется от нуля до единицы, причем чем он ближе к единице, тем сложнее выполнить данную работу в установленный срок. Самыми напряженными являются работы критического пути, для которых коэффициент напряженности равен 1. На основе значений этого коэффициента все работы СМ могут быть разделены на три группы:

– напряженные (Kн(i,j) > 0,8);

– подкритические (0,6 < Kн(i,j) < 0,8);

– резервные (Kн(i,j) < 0,6).

В результате перераспределения ресурсов стараются максимально уменьшить общую продолжительность работ, что возможно при переводе всех работ в первую группу.

Пример 3.12. Рассчитаем коэффициенты напряженности всех работ сетевой модели, рассматриваемой выше в примере 3.11. При расчете этих показателей по формуле (3.56) целесообразно пользоваться графиком данной СМ, представленным на рис. 3.7. Для работ критического пути (1, 3), (3, 4) и (4, 5) коэффициенты напряженности Кн = 1. Для других работ:

Кн(1.2)=1 -(6:(21-0)) = 0,71:

Кн(1, 4) = 1 -(9:(21-4)) = 0,47:

Кн(2, 5) = 1 -(6:(21 -0)) = 0,71.

Результаты расчетов приведены в графе 10 (Кн) табл. 3.17. Они показывают, что напряженными являются работы критического пути (1, 3), (3, 4) и (4, 5); работы (1, 2) и (2, 5) являются подкритическими, а работа (1, 4) – резервная. Следовательно, оптимизация рассматриваемой СМ возможна в основном за счет резервной работы (1, 4) и частично за счет подкритических работ (1.2) и (2, 5).

Если данный расчет СМ проведен до начала работ, менеджер проекта может скорректировать первоначальное распределение рабочих по видам работ, сняв некоторое количество рабочих с работы (1, 4) и, возможно, с работ (1, 2) и (2, 5) и распределив их по работам критического пути (1, 3), (3, 4) и (4, 5).

В результате работы, не лежащие на критическом пути, несколько увеличат свою продолжительность, а продолжительность работ критического пути сократится; тем самым при той же численности рабочих сократится срок реализации проекта в целом. Получив новый вариант сетевого графика, менеджер может повторить аналогичные расчеты, добиваясь путем перераспределения рабочих наиболее оптимального варианта СМ и, следовательно, наилучшего распределения рабочих по видам работ.

Сетевое планирование в условиях неопределенности

В рассмотренных выше примерах сроки выполнения отдельных видов работ определялись при условии взаимозаменяемости рабочих и при наличии нормативов трудоемкости для данных работ. На практике во многих случаях трудно точно определить продолжительность работ, поэтому задаются две оценки этой продолжительности – минимальная и максимальная. Минимальная оценка дает продолжительность работ при наиболее благоприятных обстоятельствах, а максимальная– при наиболее неблагоприятных. Продолжительность работы в этом случае рассматривается как случайная величина, которая при реализации может принять любое значение в заданном интервале. Такие оценки являются вероятностными, и их ожидаемые значения оцениваются по-разному в зависимости от принятого закона распределения. Так, при бета-распрсделении плотности вероятности ожидаемое значение продолжительности работ (математическое ожидание) задается формулой

(3.57)

Для характеристики степени разброса возможных значений относительно ожидаемого уровня используется показатель дисперсии:

(3.58)

На основе этих оценок можно рассчитать все характеристики СМ, однако они будут выступать как средние характеристики. При достаточно большом количестве работ можно утверждать, что общая продолжительность любого пути, включая критический, имеет нормальный закон распределения со средним значением, равным сумме средних значений продолжительности составляющих его работ, и дисперсией, равной сумме дисперсий этих же работ.

Кроме основных характеристик СМ, при вероятностном задании продолжительности работ можно решить две важные задачи:

1. определить вероятность того, что продолжительность критического пути tкр не превысит заданного (директивного) уровня Т;

2. определить максимальный срок выполнения всего комплекса работ Т при заданном уровне вероятности (надежности) р.

Более подробно вопросы сетевого планирования в условиях неопределенности с решением конкретных примеров рассмотрены в ряде учебных и научных изданий (см., например, параграф 3.6 в 1151).